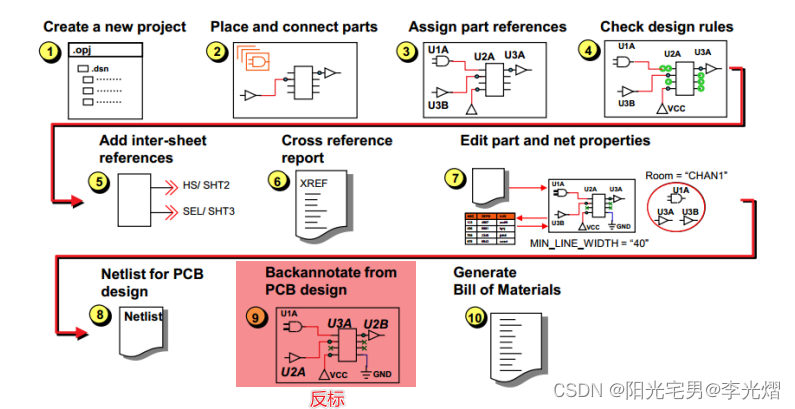
Tokitsukaze and Bracelet
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
题目描述
《绯染天空》是一款由 key 社与飞机社共同开发的角色扮演游戏,剧情内容由著名的剧本作家麻枝准编写。它是一款氪金手游,但也有 steam 端。直至今日(2024.2.5),Tokitsukaze 入坑短短6个月,时长却已达到了382小时。

游戏中有着一个''饰品炼成''系统,通过消耗宝石,可以炼成对应的饰品。''饰品炼成''系统有关手环的信息介绍如下:
手环有 333 种属性:普通攻击百分比加成,体力,精神。每次炼成手环时,会对手环的每个属性都随机赋予强化等级,每个属性的强化等级可能为+0+0+0, +1+1+1, +2+2+2。强化等级对应的属性值如下:
- 对于普通攻击百分比加成来说:+0+0+0 为 100%100\%100%,+1+1+1 为 150%150\%150%,+2+2+2 为 200%200\%200%;
- 对于体力和精神来说:+0+0+0 会在 {29,30,31,32}\{29,30,31,32\}{29,30,31,32} 里随机选择,+1+1+1 会在 {34,36,38,40}\{34,36,38,40\}{34,36,38,40} 里随机选择, +2+2+2 固定为 454545。
例如,一个普通攻击百分比加成 100%100\%100%,体力 454545,精神 404040 的手环的强化等级为 +3+3+3。其中普通攻击力百分比提供了 +0+0+0,体力提供了 +2+2+2,精神提供了 +1+1+1。
下图是一个顶级属性的手环:

现在 Tokitsukaze 炼成了 nnn 个手环,她只知道每个手环的属性,请你告诉她每个手环的强化等级是多少。
输入描述:
第一行包含一个整数 nnn (1≤n≤1001 \leq n \leq 1001≤n≤100),表示 Tokitsukaze 炼成了 nnn 个手环。
接下来 nnn 行,每行三个整数 aia_iai, bib_ibi, cic_ici (ai∈{100,150,200}a_i \in \{100,150,200\}ai∈{100,150,200}; bib_ibi, ci∈{29,30,31,32,34,36,38,40,45}c_i \in \{29,30,31,32,34,36,38,40,45\}ci∈{29,30,31,32,34,36,38,40,45}),表示第 iii 个手环的数值:普通攻击百分比加成 ai%a_i\%ai%, 体力 bib_ibi, 精神 cic_ici。
输出描述:
输出 nnn 行,每行包含一个整数,第 iii 行表示第 iii 个手环的强化等级。
示例1
输入
复制5 100 29 29 100 32 38 150 45 40 200 45 45 100 45 40
5 100 29 29 100 32 38 150 45 40 200 45 45 100 45 40
输出
复制0 1 4 6 3
0 1 4 6 3
说明
样例解释: 第 111 个手环的属性为:普通攻击百分比加成 100%100\%100%,体力 292929,精神 292929。普通攻击力百分比提供了 +0+0+0,体力提供了 +0+0+0,精神提供了 +0+0+0,所以该手环的强化等级为 +0+0+0; 第 222 个手环的属性为:普通攻击百分比加成 100%100\%100%,体力 323232,精神 383838。普通攻击力百分比提供了 +0+0+0,体力提供了 +0+0+0,精神提供了 +1+1+1,所以该手环的强化等级为 +1+1+1; 第 333 个手环的属性为:普通攻击百分比加成 150%150\%150%,体力 454545,精神 404040。普通攻击力百分比提供了 +1+1+1,体力提供了 +2+2+2,精神提供了 +1+1+1,所以该手环的强化等级为 +4+4+4; 第 444 个手环的属性为:普通攻击百分比加成 200%200\%200%,体力 454545,精神 454545。普通攻击力百分比提供了 +2+2+2,体力提供了 +2+2+2,精神提供了 +2+2+2,所以该手环的强化等级为 +6+6+6; 第 555 个手环的属性为:普通攻击百分比加成 100%100\%100%,体力 454545,精神 404040。普通攻击力百分比提供了 +0+0+0,体力提供了 +2+2+2,精神提供了 +1+1+1,所以该手环的强化等级为 +3+3+3。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,a,b,c,x;
cin>>n;
while(n--){
x=0;
cin>>a>>b>>c;
if(a==150)x+=1;
if(a==200)x+=2;
if(b==34||b==36||b==38||b==40)x+=1;
if(b==45)x+=2;
if(c==34||c==36||c==38||c==40)x+=1;
if(c==45)x+=2;
cout<<x<<endl;
}
return 0;
}Tokitsukaze and Cats
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
Tokitsukaze 家里有 kkk 只猫。现实中 kkk 为 555(与本题无关),如下图所示:

众所周知 Tokitsukaze 特别懒,在家从不搞卫生,搞卫生这事都是由 Tokitsukaze 的老婆 TomiokapEace 一手包办。在 TomiokapEace 搞卫生时,它们总是会上窜下跳,特别碍事,于是她想做一些措施让它们无法移动。
现在把 Tokitsukaze 的家看作是一个 n×mn \times mn×m 的网格,第 iii 只猫的位置在 (xi,yi)(x_i,y_i)(xi,yi)。TomiokapEace 想用若干片防猫网来限制猫的移动,她将在一只猫所在格子的四周各放上一片防猫网。
一片防猫板是位于两个相邻格子间隔,长度为1个单位的障碍物,可以阻止猫移动。具体来讲,当猫位于 (x,y)(x,y)(x,y) 时,若(x−1,y)(x-1,y)(x−1,y), (x,y−1)(x,y-1)(x,y−1), (x+1,y)(x+1,y)(x+1,y), (x,y+1)(x,y+1)(x,y+1) 中的任意一格和 (x,y)(x,y)(x,y) 之间不存在防猫板,则猫可以向相邻格子移动。
TomiokapEace 想知道至少需要购买多少片防猫网才能使所有猫无法移动。
PS:现实中确实买了防猫网,塑料的,上面有尖尖的刺。本以为它们不敢踩上去,谁知道根本防不了一点,直接给你表演精准踩到刺与刺的空隙间。对于它们来说,这玩意也只不过是一个减速带罢了(悲)。
输入描述:
第一行包含三个整数 nnn, mmm, kkk (1≤n,m≤3001 \leq n, m \leq 3001≤n,m≤300; 1≤k≤n⋅m1 \leq k \leq n \cdot m1≤k≤n⋅m),表示 Tokitsukaze 家的大小为 n×mn \times mn×m,以及家里有 kkk 只猫。 接下来 kkk 行,每行两个整数 xix_ixi, yiy_iyi (1≤xi≤n1 \leq x_i \leq n1≤xi≤n; 1≤yi≤m1 \leq y_i \leq m1≤yi≤m),表示第 iii 只猫的位置。保证所有猫的位置互不相同。
输出描述:
输出一个整数,表示 TomiokapEace 至少需要购买防猫网的数量。
示例1
输入
复制5 4 3 3 2 4 3 4 4
5 4 3 3 2 4 3 4 4
输出
复制11
11
说明
样例1如图,这三只猫至少需要 111111 片防猫网(黑色边界为防猫网)。你可以认为每只猫是独立的,可以随便移动,移动到别的猫所在位置也算移动。所以即使两只猫相邻,中间也需要有防猫网。
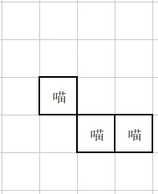
示例2
输入
复制1 1 1 1 1
1 1 1 1 1
输出
复制4
4
//把重复的边删掉就行
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,m,k,z=0,x,y,a[305][305]={0};
cin>>n>>m>>k;
z=k*4;
while(k--){
cin>>x>>y;
a[x][y]=1;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i][j]){
if(a[i+1][j])z--;
if(a[i][j+1])z--;
//只需要判断当前位置的下边和右边,因为i循环就是从上到下,j循环就是从左到右
}
}
}
cout<<z;
return 0;
}Tokitsukaze and Eliminate (easy) 链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
easy 与 hard 的唯一区别是 colicol_icoli 的范围。
Tokitsukaze 正在玩一个消除游戏。
初始有 nnn 个宝石从左到右排成一排,第 iii 个宝石的颜色为 colicol_icoli。Tokitsukaze 可以进行若干次以下操作:
- 任选一种颜色 xxx,将颜色为 xxx 的最右边那颗宝石、以及该宝石右边的所有宝石全部消除。
Tokitsukaze 想知道至少需要几次操作才能把 nnn 个宝石全部消除。
输入描述:
第一行包含一个整数 TTT (1≤T≤2⋅1051 \leq T \leq 2 \cdot 10^51≤T≤2⋅105),表示 TTT 组测试数据。 对于每组测试数据: 第一行包含一个整数 nnn (1≤n≤2⋅1051 \leq n \leq 2 \cdot 10^51≤n≤2⋅105),表示初始宝石的数量。 第二行包含 nnn 个整数 col1,col2,…,colncol_1, col_2, \ldots, col_ncol1,col2,…,coln (1≤coli≤min(n,2)1 \leq col_i \leq \min(n,2)1≤coli≤min(n,2)),表示每个宝石的颜色。 保证 ∑n\sum n∑n 不超过 2⋅1052 \cdot 10^52⋅105。
输出描述:
对于每组测试数据,输出一个整数,表示把 nnn 个宝石全部消除所需要的最少操作次数。
示例1
输入
复制4 3 1 2 1 5 1 2 2 1 2 11 2 2 1 2 2 1 1 2 2 1 2 1 1
4 3 1 2 1 5 1 2 2 1 2 11 2 2 1 2 2 1 1 2 2 1 2 1 1
输出
复制2 2 6 1
2 2 6 1
说明
第一组测试数据: 初始宝石为 [1,2,1][1,2,1][1,2,1]; 第 111 次操作选择颜色 222,可以消除最右边的 222 个宝石,当前剩余宝石为 [1][1][1]; 第 222 次操作选择颜色 111,即可把所有宝石都消除。 第三组测试数据: 初始宝石为 [2,2,1,2,2,1,1,2,2,1,2][2,2,1,2,2,1,1,2,2,1,2][2,2,1,2,2,1,1,2,2,1,2]; 第 111 次操作选择颜色 111,可以消除最右边的 222 个宝石,当前剩余宝石为 [2,2,1,2,2,1,1,2,2][2,2,1,2,2,1,1,2,2][2,2,1,2,2,1,1,2,2]; 第 222 次操作选择颜色 111,可以消除最右边的 333 个宝石,当前剩余宝石为 [2,2,1,2,2,1][2,2,1,2,2,1][2,2,1,2,2,1]; 第 333 次操作选择颜色 222,可以消除最右边的 222 个宝石,当前剩余宝石为 [2,2,1,2][2,2,1,2][2,2,1,2]; 第 444 次操作选择颜色 111,可以消除最右边的 222 个宝石,当前剩余宝石为 [2,2][2,2][2,2]; 第 555 次操作选择颜色 222,可以消除最右边的 111 个宝石,当前剩余宝石为 [2][2][2]; 第 666 次操作选择颜色 222,即可把所有宝石都消除
//待定。
Tokitsukaze and Short Path (plus)链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
plus 与 minus 的唯一区别是 边权的计算方式。
Tokitsukaze 有一张 nnn 个顶点的完全图 GGG, 顶点编号是 111 到 nnn,编号为 iii 的顶点的值是 aia_iai。
完全图指的是每对顶点之间都恰好有一条无向边的图。对于顶点 uuu 和顶点 vvv 之间的无向边,边权计算方式如下:
wu,v={0,u=v∣au+av∣+∣au−av∣,u≠vw_{u,v}=\begin{cases} 0, & u = v \\ |a_u+a_v|+|a_u-a_v|, & u \ne v \end{cases}wu,v={0,∣au+av∣+∣au−av∣,u=vu=v
定义 dist(i,j)dist(i,j)dist(i,j) 表示顶点 iii 为起点,顶点 jjj 为终点的最短路。求 ∑i=1n∑j=1ndist(i,j)\sum_{i=1}^n \sum_{j=1}^n dist(i,j)∑i=1n∑j=1ndist(i,j)
关于最短路的定义:
定义一条从 sss 到 ttt 的路径为若干条首尾相接的边形成的序列且该序列的第一条边的起点为 sss,最后一条边的终点为 ttt,特别的,当 s=ts=ts=t 时该序列可以为空。
定义一条从 sss 到 ttt 的路径长度为该路径中边权的总和。
定义 sss 到 ttt 的最短路为 sss 到 ttt 所有路径长度中的最小值。
输入描述:
第一行包含一个整数 TTT (1≤T≤2⋅1051 \leq T \leq 2\cdot 10^51≤T≤2⋅105),表示 TTT 组测试数据。 对于每组测试数据: 第一行包含一个整数 nnn (1≤n≤2⋅1051 \leq n \leq 2\cdot 10^51≤n≤2⋅105),表示完全图 GGG 的顶点数量。 第二行包含 nnn 个整数 a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an (1≤ai≤2⋅1051 \leq a_i \leq 2\cdot 10^51≤ai≤2⋅105),表示完全图 GGG 的每个顶点的值。 保证 ∑n\sum n∑n 不超过 2⋅1052 \cdot 10^52⋅105。
输出描述:
对于每组测试数据,输出一个整数表示答案。
示例1
输入
复制5 1 1 3 10 1 100 5 1 2 3 4 5 4 2 3 5 8 5 1 3 3 4 5
5 1 1 3 10 1 100 5 1 2 3 4 5 4 2 3 5 8 5 1 3 3 4 5
输出
复制0 840 160 148 164
0 840 160 148 164
说明
第二组测试数据,图 GGG 如下:
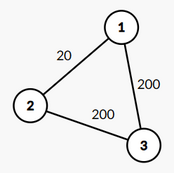
显然,dist(1,2)=w1,2=20dist(1,2)=w_{1,2}=20dist(1,2)=w1,2=20, dist(1,3)=w1,3=200dist(1,3)=w_{1,3}=200dist(1,3)=w1,3=200, dist(2,3)=w2,3=200dist(2,3)=w_{2,3}=200dist(2,3)=w2,3=200。
所以 ∑i=1n∑j=1ndist(i,j)=840\sum_{i=1}^n \sum_{j=1}^n dist(i,j)=840∑i=1n∑j=1ndist(i,j)=840
//一般代码会超时。以 n=4,分别是1,2,3,4为例,得到dist(1,2)=4,sist(1,3)=6,dist(1,4)=8,dist(2,3)=6,dist(2,4)=8,dist(3,4)=8,
最后(4+6+6+8+8+8)*2得到输出结果。
我们可以发现三个点,第一,每个dist的值其实是较大的那个数的两倍;第二,(4+6+6+8+8+8)也就是3个8,2个6,1个4,对应n-1个2*a[n-1],以此类推;第三,加起来*2得到最终结果。
#include<bits/stdc++.h>
using namespace std;
int main(){
long long t,n,i,j,a[200005];
cin>>t;
while(t--){
long long y=0;
cin>>n;
if(n==1){int x;cin>>x;cout<<"0\n";continue;}
for(i=0;i<n;i++)cin>>a[i];
sort(a,a+n);
for(i=n-1;i>0;i--){//关键代码,主要通过找规律
y+=i*(2*a[i]);
}
cout<<y*2<<endl;
}
return 0;
}Tokitsukaze and Short Path (minus)链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
plus 与 minus 的唯一区别是 边权的计算方式。
Tokitsukaze 有一张 nnn 个顶点的完全图 GGG, 顶点编号是 111 到 nnn,编号为 iii 的顶点的值是 aia_iai。
完全图指的是每对顶点之间都恰好有一条无向边的图。对于顶点 uuu 和顶点 vvv 之间的无向边,边权计算方式如下:
wu,v={0,u=v∣au+av∣−∣au−av∣,u≠vw_{u,v}=\begin{cases} 0, & u = v \\ |a_u+a_v|-|a_u-a_v|, & u \ne v \end{cases}wu,v={0,∣au+av∣−∣au−av∣,u=vu=v
定义 dist(i,j)dist(i,j)dist(i,j) 表示顶点 iii 为起点,顶点 jjj 为终点的最短路。求 ∑i=1n∑j=1ndist(i,j)\sum_{i=1}^n \sum_{j=1}^n dist(i,j)∑i=1n∑j=1ndist(i,j)
关于最短路的定义:
定义一条从 sss 到 ttt 的路径为若干条首尾相接的边形成的序列且该序列的第一条边的起点为 sss,最后一条边的终点为 ttt,特别的,当 s=ts=ts=t 时该序列可以为空。
定义一条从 sss 到 ttt 的路径长度为该路径中边权的总和。
定义 sss 到 ttt 的最短路为 sss 到 ttt 所有路径长度中的最小值。
输入描述:
第一行包含一个整数 TTT (1≤T≤2⋅1051 \leq T \leq 2\cdot 10^51≤T≤2⋅105),表示 TTT 组测试数据。 对于每组测试数据: 第一行包含一个整数 nnn (1≤n≤2⋅1051 \leq n \leq 2\cdot 10^51≤n≤2⋅105),表示完全图 GGG 的顶点数量。 第二行包含 nnn 个整数 a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an (1≤ai≤2⋅1051 \leq a_i \leq 2\cdot 10^51≤ai≤2⋅105),表示完全图 GGG 的每个顶点的值。 保证 ∑n\sum n∑n 不超过 2⋅1052 \cdot 10^52⋅105。
输出描述:
对于每组测试数据,输出一个整数表示答案。
示例1
输入
复制5 1 1 3 10 1 100 5 1 2 3 4 5 4 2 3 5 8 5 1 3 3 4 5
5 1 1 3 10 1 100 5 1 2 3 4 5 4 2 3 5 8 5 1 3 3 4 5
输出
复制0 16 64 64 64
0 16 64 64 64
说明
第二组测试数据,图 GGG 如下:
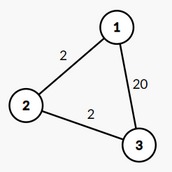
显然,dist(1,2)=w1,2=2dist(1,2)=w_{1,2}=2dist(1,2)=w1,2=2, dist(1,3)=w1,2+w2,3=4dist(1,3)=w_{1,2}+w_{2,3}=4dist(1,3)=w1,2+w2,3=4, dist(2,3)=w2,3=2dist(2,3)=w_{2,3}=2dist(2,3)=w2,3=2。
所以 ∑i=1n∑j=1ndist(i,j)=16\sum_{i=1}^n \sum_{j=1}^n dist(i,j)=16∑i=1n∑j=1ndist(i,j)=16
//和上面一题的区别就是计算方式不同。 同样的,我们以 n=4,分别是1,2,3,4为例,得到dist(1,2)=2,sist(1,3)=2,dist(1,4)=2,dist(2,3)=4,dist(2,4)=4,dist(3,4)=6,这里根据最短距离,dist(3,4)可以=dist(1,3)+dist(1,4)=4,那么,我们我们发现,有时候dist(i,j)>dist(1,i)+dist(1,j),所以要去比较dist(i,j)和4*a[0],也就是a[i-1]和2*a[0].
最后(2+2+2+4+4+4)*2得到输出结果。
#include<bits/stdc++.h>
using namespace std;
int main(){
long long t,n,i,j,a[200005];
cin>>t;
while(t--){
long long y=0;
cin>>n;
if(n==1){int x;cin>>x;cout<<"0\n";continue;}
for(i=0;i<n;i++)cin>>a[i];
sort(a,a+n);
for(i=1;i<n;i++){
y+=(n-i)*min(2*a[0],a[i-1])*2;
}
cout<<y*2<<endl;
}
return 0;
}