数字盒子
问题描述
你有一个盒子,你可以往里面放数,也可以从里面取出数。
初始时,盒子是空的,你会依次做 Q 个操作,操作分为两类:
- 插入操作:询问盒子中是否存在数 x,如果不存在则把数 x 丢到盒子里。
- 删除操作:询问盒子中是否存在数 x,如果存在则取出 x。
对于每个操作,你需要输出是否成功插入或删除。
输入格式
第一行一个正整数 Q,表示操作个数。
接下来 Q 行依次描述每个操作。每行 2 个用空格隔开的非负整数 op,x 描述一个操作:op 表示操作类型,op=1 则表示这是一个插入操作,op=2 则表示这是一个删除操作;x 的意义与操作类型有关,具体见题目描述。
输出格式
按顺序对所有操作输出,对于每个操作输出一行,如果成功则输出“Succeeded”(不含引号),如果失败则输出“Failed”(不含引号)。
样例输入
6
1 100
1 100
2 100
1 200
2 100
2 200
样例输出
Succeeded
Failed
Succeeded
Succeeded
Failed
Succeeded
数据范围
对于 60% 的数据,保证 x<10^5。
对于 100% 的数据,保证 x<10^18,Q≤5*10^5。
对于所有数据,保证 op∈{1,2}。
时间限制:1 s
空间限制:256 MB
提示
[对于 x 较小的情况,我们只需要用数组记录每个数是否在盒子里即可。]
[对于 x 较大的情况,我们可不可以用什么方法把它们“变小”呢?可以想想哈希表哦!]
代码实现
class Box:
def __init__(self):
self.contents = set()
def insert(self, x):
if x not in self.contents:
self.contents.add(x)
return "Succeeded"
else:
return "Failed"
def remove(self, x):
if x in self.contents:
self.contents.remove(x)
return "Succeeded"
else:
return "Failed"
def main():
q = int(input())
box = Box()
for _ in range(q):
op, x = map(int, input().split())
if op == 1:
result = box.insert(x)
elif op == 2:
result = box.remove(x)
print(result)
if __name__ == "__main__":
main()
重编码
问题描述

输入格式

输出格式
输出一行一个整数,表示整篇文章重编码后的最短长度。
样例输入
4
1
1
2
2
样例输出
12
样例解释
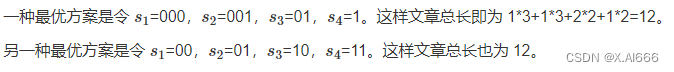
数据范围

提示
[我们希望越长的串出现次数越少,那么贪心地考虑,让出现次数少的串更长。]
[于是我们先区分出出现次数最少的 2 个串,在它们的开头分别添加 0 和 1。]
[接着,由于它们已经被区分(想一想,为什么?),所以我们可以把它们看作是**一个**单词,且其出现次数为它们的和,然后继续上面的“添数”和“合并”操作。]
[这样,我们不停地“合并单词”,直到只剩 1 个单词,即可结束。]
[可以证明这是最优的。]
代码实现
import heapq
# 这是求解整个问题的函数
# 返回值:答案
def get_answer():
n = int(input())
w = [int(input()) for _ in range(n)]
# 将所有w加入优先队列pq中
pq = []
for i in range(n):
heapq.heappush(pq, w[i])
sum_val = 0 # 置零返回值
while len(pq) > 1: # 当pq中仍有超过多少元素时进行循环呢?
new_ele = 0 # 这是本次合并后将要加入队列的新元素
# 从pq中取出最小的两个元素并合并
for k in range(2):
new_ele += heapq.heappop(pq)
sum_val += new_ele # 将本次合并对答案的贡献加入答案
heapq.heappush(pq, new_ele) # 将新元素加入队列
return sum_val # 返回答案
# 获取答案并输出
result = get_answer()
print(result)
成绩排序
问题描述
有 n 名学生,它们的学号分别是 1,2,…,n。这些学生都选修了邓老师的算法训练营、数据结构训练营这两门课程。
学期结束了,所有学生的课程总评都已公布,所有总评分数都是 [0,100] 之间的整数。巧合的是,不存在两位同学,他们这两门课的成绩都完全相同。
邓老师希望将这些所有的学生按这两门课程的总分进行降序排序,特别地,如果两位同学的总分相同,那邓老师希望把算法训练营得分更高的同学排在前面。由于上面提到的巧合,所以,这样排名就可以保证没有并列的同学了。
邓老师将这个排序任务交给了他的助教。可是粗心的助教没有理解邓老师的要求,将所有学生按学号进行了排序。
邓老师希望知道,助教的排序结果中,存在多少逆序对。
如果对于两个学生 (i,j) 而言,i 被排在了 j 前面,并且i 本应被排在 j 的后面,我们就称 (i,j) 是一个逆序对。
请你先帮邓老师把所有学生按正确的顺序进行排名,再告诉他助教的错误排名中逆序对的数目。
输入格式
第一行一个整数 n,表示学生的个数。
第 2 行到第 n+1 行,每行 2 个用空格隔开的非负整数,第 i+1 行的两个数依次表示学号为 i 的同学的算法训练营、数据结构训练营的总评成绩。
输出格式
输出包含 n+1 行。
前 n 行表示正确的排序结果,每行 4 个用空格隔开的整数,第 i 行的数依次表示排名为 i 的同学的学号、总分、算法训练营成绩、数据结构训练营成绩。
第 n+1 行一个整数,表示助教的错误排名中逆序对的数目。
样例输入
3
95 85
90 90
100 99
样例输出
3 199 100 99
1 180 95 85
2 180 90 90
2
样例解释
学号为 3 的同学总分为 199,是最高的,所以他应该排第一名。
学号为 1 的同学虽然总分与学号为 2 的同学一致,但是他的算法训练营成绩更高,所以在排名规则下更胜一筹。
原错误排名中的逆序对数目为 2 ,这些逆序对分别为 (1,3) 和 (2,3)。
数据范围
对于 25% 的数据,保证 n=3。
对于 50% 的数据,保证 n≤10。
对于另外 25% 的数据,保证所有同学的总分两两不同。
对于 100% 的数据,保证 n≤5,000 ,且保证不存在成绩完全相同的学生。
时间限制:10 sec
空间限制:256 MB
提示
[可以使用起泡排序将所有学生进行排名。]
[善良的助教提醒你,在起泡排序的过程中,每次交换都会使逆序对数目减少 1 哦!想一想,为什么?]
这道题可以设计出时间复杂度为 O(nlogn) 的算法。]
代码实现
def bubble_sort(arr):
n = len(arr)
inversion_count = 0
for i in range(n):
for j in range(0, n-i-1):
# 如果当前学生的总分更高,或者总分相同但算法训练营成绩更高,进行交换
if arr[j][1] < arr[j+1][1] or (arr[j][1] == arr[j+1][1] and arr[j][2] < arr[j+1][2]):
arr[j], arr[j+1] = arr[j+1], arr[j]
inversion_count += 1
return inversion_count
# 输入
n = int(input())
students = []
for i in range(1, n+1):
scores = list(map(int, input().split()))
students.append((i, scores[0] + scores[1], scores[0], scores[1]))
# 使用气泡排序对倒序进行排序和计数
inversion_count = bubble_sort(students)
# 输出正确排名
for i in range(n):
print(f"{students[i][0]} {students[i][1]} {students[i][2]} {students[i][3]}")
# 输出助教错误排名中的逆序对数目
print(inversion_count)

![【洛谷题解】P1075 [NOIP2012 普及组] 质因数分解](https://img-blog.csdnimg.cn/direct/d50563c06e914a84a2ae3f7824f8cda6.png)