【leetcode热题100】最大矩形

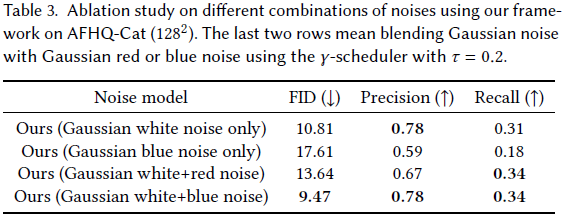
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

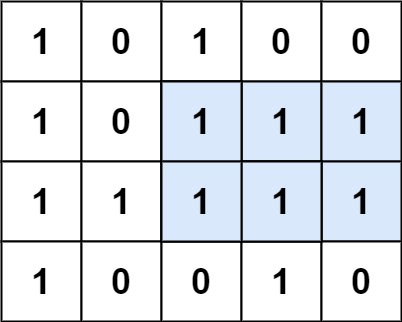
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = [["0"]]
输出：0

示例 3：

输入：matrix = [["1"]]
输出：1

解法一暴力破解

参考这里-solution-for-your-reference>)，遍历每个点，求以这个点为矩阵右下角的所有矩阵面积。如下图的两个例子，橙色是当前遍历的点，然后虚线框圈出的矩阵是其中一个矩阵。

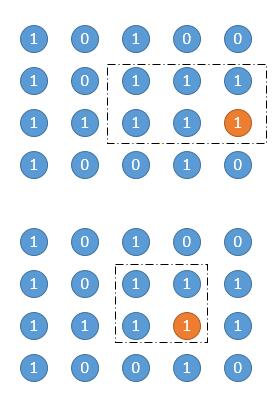
怎么找出这样的矩阵呢？如下图，如果我们知道了以这个点结尾的连续 1 的个数的话，问题就变得简单了。

首先求出高度是 1 的矩形面积，也就是它自身的数，也就是上图以橙色的 4 结尾的「1234」的那个矩形，面积就是 4。
然后向上扩展一行，高度增加一，选出当前列最小的数字，作为矩阵的宽，如上图，当前列中有 2 和 4 ，那么，就将 2 作为矩形的宽，求出面积，对应上图的矩形圈出的部分。
然后继续向上扩展，重复步骤 2。

按照上边的方法，遍历所有的点，以当前点为矩阵的右下角，求出所有的矩阵就可以了。下图是某一个点的过程。

以橙色的点为右下角，高度为 1。

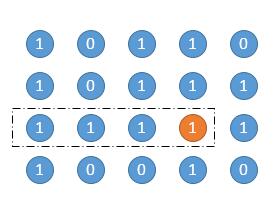
高度为 2。

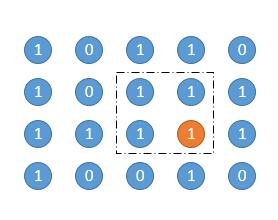
高度为 3。

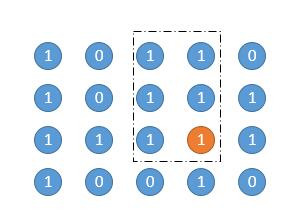
代码的话，把求每个点累计的连续 1 的个数用 width 保存，同时把求最大矩形的面积和求 width融合到同一个循环中。

public int maximalRectangle(char[][] matrix) {
    if (matrix.length == 0) {
        return 0;
    }
    //保存以当前数字结尾的连续 1 的个数
    int[][] width = new int[matrix.length][matrix[0].length];
    int maxArea = 0;
    //遍历每一行
    for (int row = 0; row < matrix.length; row++) {
        for (int col = 0; col < matrix[0].length; col++) {
            //更新 width
            if (matrix[row][col] == '1') {
                if (col == 0) {
                    width[row][col] = 1;
                } else {
                    width[row][col] = width[row][col - 1] + 1;
                }
            } else {
                width[row][col] = 0;
            }
            //记录所有行中最小的数
            int minWidth = width[row][col];
            //向上扩展行
            for (int up_row = row; up_row >= 0; up_row--) {
                int height = row - up_row + 1;
                //找最小的数作为矩阵的宽
                minWidth = Math.min(minWidth, width[up_row][col]);
                //更新面积
                maxArea = Math.max(maxArea, height * minWidth);
            }
        }
    }
    return maxArea;
}

时间复杂度：O（m²n）。

空间复杂度：O（mn）。

解法二

参考这里-solution-based-on-Largest-Rectangle-in-Histogram>)，接下来的解法，会让这道题变得异常简单。还记得 84 题吗？求一个直方图矩形的最大面积。

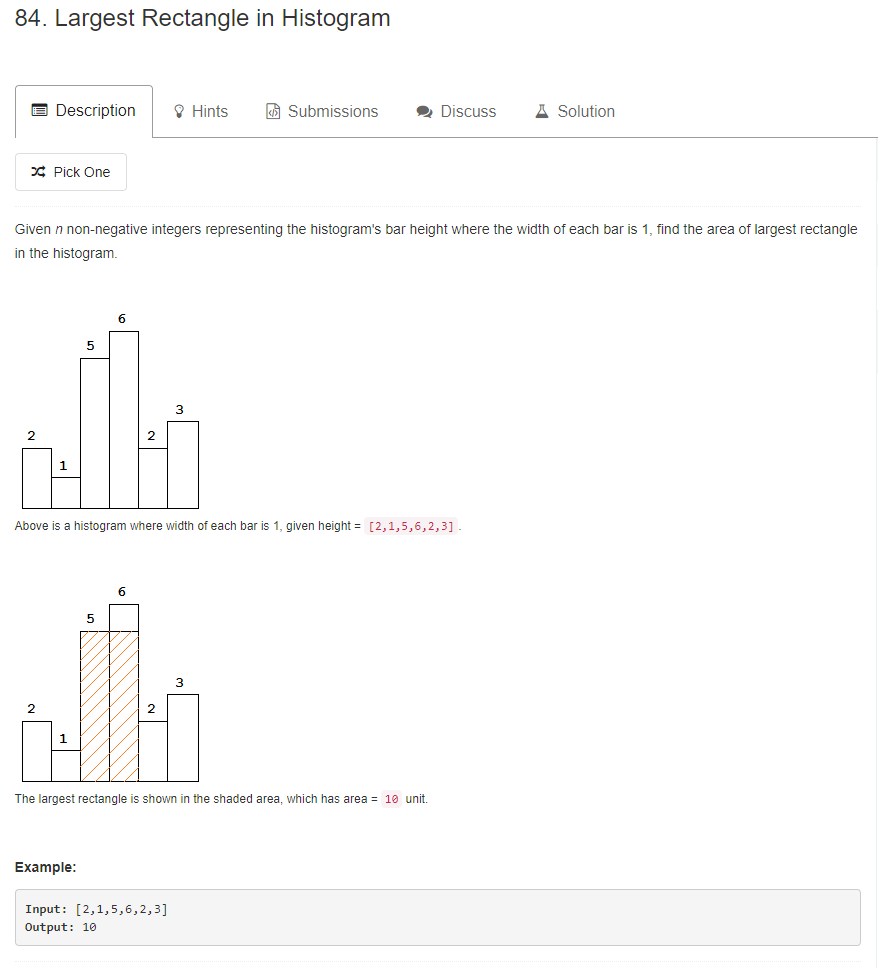
大家可以先做 84 题，然后回来考虑这道题。

再想一下这个题，看下边的橙色的部分，这完全就是上一道题呀！

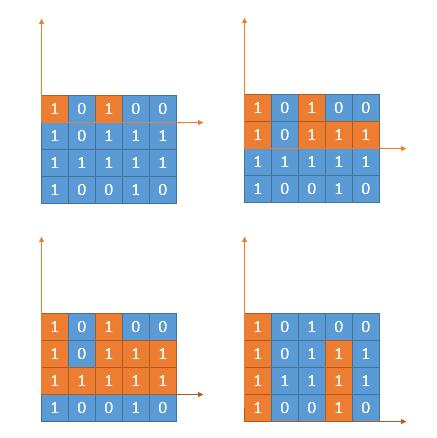
算法有了，就是求出每一层的 heights[] 然后传给上一题的函数就可以了。

利用上一题的栈解法。

public int maximalRectangle(char[][] matrix) {
    if (matrix.length == 0) {
        return 0;
    }
    int[] heights = new int[matrix[0].length];
    int maxArea = 0;
    for (int row = 0; row < matrix.length; row++) {
        //遍历每一列，更新高度
        for (int col = 0; col < matrix[0].length; col++) {
            if (matrix[row][col] == '1') {
                heights[col] += 1;
            } else {
                heights[col] = 0;
            }
        }
        //调用上一题的解法，更新函数
        maxArea = Math.max(maxArea, largestRectangleArea(heights));
    }
    return maxArea;
}

public int largestRectangleArea(int[] heights) {
    int maxArea = 0;
    Stack<Integer> stack = new Stack<>();
    int p = 0;
    while (p < heights.length) {
        //栈空入栈
        if (stack.isEmpty()) {
            stack.push(p);
            p++;
        } else {
            int top = stack.peek();
            //当前高度大于栈顶，入栈
            if (heights[p] >= heights[top]) {
                stack.push(p);
                p++;
            } else {
                //保存栈顶高度
                int height = heights[stack.pop()];
                //左边第一个小于当前柱子的下标
                int leftLessMin = stack.isEmpty() ? -1 : stack.peek();
                //右边第一个小于当前柱子的下标
                int RightLessMin = p;
                //计算面积
                int area = (RightLessMin - leftLessMin - 1) * height;
                maxArea = Math.max(area, maxArea);
            }
        }
    }
    while (!stack.isEmpty()) {
        //保存栈顶高度
        int height = heights[stack.pop()];
        //左边第一个小于当前柱子的下标
        int leftLessMin = stack.isEmpty() ? -1 : stack.peek();
        //右边没有小于当前高度的柱子，所以赋值为数组的长度便于计算
        int RightLessMin = heights.length;
        int area = (RightLessMin - leftLessMin - 1) * height;
        maxArea = Math.max(area, maxArea);
    }
    return maxArea;
}

时间复杂度：O（mn）。

空间复杂度：O（n）。

利用上一题的解法四。

public int maximalRectangle(char[][] matrix) {
    if (matrix.length == 0) {
        return 0;
    }
    int[] heights = new int[matrix[0].length];
    int maxArea = 0;
    for (int row = 0; row < matrix.length; row++) {
        //遍历每一列，更新高度
        for (int col = 0; col < matrix[0].length; col++) {
            if (matrix[row][col] == '1') {
                heights[col] += 1;
            } else {
                heights[col] = 0;
            }
        }
        //调用上一题的解法，更新函数
        maxArea = Math.max(maxArea, largestRectangleArea(heights));
    }
    return maxArea;
}

public int largestRectangleArea(int[] heights) {
    if (heights.length == 0) {
        return 0;
    }
    int[] leftLessMin = new int[heights.length];
    leftLessMin[0] = -1;
    for (int i = 1; i < heights.length; i++) {
        int l = i - 1;
        while (l >= 0 && heights[l] >= heights[i]) {
            l = leftLessMin[l];
        }
        leftLessMin[i] = l;
    }

    int[] rightLessMin = new int[heights.length];
    rightLessMin[heights.length - 1] = heights.length;
    for (int i = heights.length - 2; i >= 0; i--) {
        int r = i + 1;
        while (r <= heights.length - 1 && heights[r] >= heights[i]) {
            r = rightLessMin[r];
        }
        rightLessMin[i] = r;
    }
    int maxArea = 0;
    for (int i = 0; i < heights.length; i++) {
        int area = (rightLessMin[i] - leftLessMin[i] - 1) * heights[i];
        maxArea = Math.max(area, maxArea);
    }
    return maxArea;
}

时间复杂度：O（mn）。

空间复杂度：O（n）。

解法三

解法二中套用的栈的解法，我们其实可以不用调用函数，而是把栈糅合到原来求 heights 中。因为栈的话并不是一次性需要所有的高度，所以可以求出一个高度，然后就操作栈。

public int maximalRectangle(char[][] matrix) {
    if (matrix.length == 0) {
        return 0;
    }
    int[] heights = new int[matrix[0].length + 1]; //小技巧后边讲
    int maxArea = 0;
    for (int row = 0; row < matrix.length; row++) {
        Stack<Integer> stack = new Stack<Integer>();
        heights[matrix[0].length] = 0;
        //每求一个高度就进行栈的操作
        for (int col = 0; col <= matrix[0].length; col++) {
            if (col < matrix[0].length) { //多申请了 1 个元素，所以要判断
                if (matrix[row][col] == '1') {
                    heights[col] += 1;
                } else {
                    heights[col] = 0;
                }
            }
            if (stack.isEmpty() || heights[col] >= heights[stack.peek()]) {
                stack.push(col);
            } else {
                //每次要判断新的栈顶是否高于当前元素
                while (!stack.isEmpty() && heights[col] < heights[stack.peek()]) {
                    int height = heights[stack.pop()];
                    int leftLessMin = stack.isEmpty() ? -1 : stack.peek();
                    int RightLessMin = col;
                    int area = (RightLessMin - leftLessMin - 1) * height;
                    maxArea = Math.max(area, maxArea);
                }
                stack.push(col);
            }
        }

    }
    return maxArea;
}

时间复杂度：O（mn）。

空间复杂度：O（n）。

里边有一个小技巧，84 题的栈解法中，我们用了两个 while 循环，第二个 while 循环用来解决遍历完元素栈不空的情况。其实，我们注意到两个 while 循环的逻辑完全一样的。所以我们可以通过一些操作，使得遍历结束后，依旧进第一个 while 循环，从而剩下了第 2 个 while 循环，代码看起来会更简洁。

那就是 heights 多申请一个元素，赋值为 0。这样最后一次遍历的时候，栈顶肯定会大于当前元素，所以就进入了第一个 while 循环。

解法四动态规划

参考这里，这是 leetcode Solution 中投票最高的，但比较难理解，但如果结合 84 题去想的话就很容易了。

解法二中，用了 84 题的两个解法，解法三中我们把栈糅合进了原算法，那么另一种可以一样的思路吗？不行！因为栈不要求所有的高度，可以边更新，边处理。而另一种，是利用两个数组， leftLessMin [ ] 和 rightLessMin [ ]。而这两个数组的更新，是需要所有高度的。

解法二中，我们更新一次 heights，就利用之前的算法，求一遍 leftLessMin [ ] 和 rightLessMin [ ]，然后更新面积。而其实，我们求 leftLessMin [ ] 和 rightLessMin [ ] 可以利用之前的 leftLessMin [ ] 和 rightLessMin [ ] 来更新本次的。

我们回想一下 leftLessMin [ ] 和 rightLessMin [ ] 的含义， leftLessMin [ i ] 代表左边第一个比当前柱子矮的下标，如下图橙色柱子时当前遍历的柱子。rightLessMin [ ] 时右边第一个。

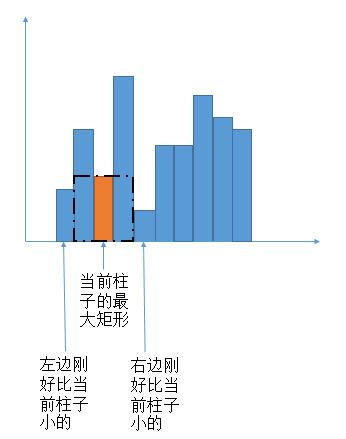
left 和 right 是对称关系，下边只考虑 left 的求法。

如下图，如果当前新增的层全部是 1，当然这时最完美的情况，那么 leftLessMin [ ] 根本不需要改变。

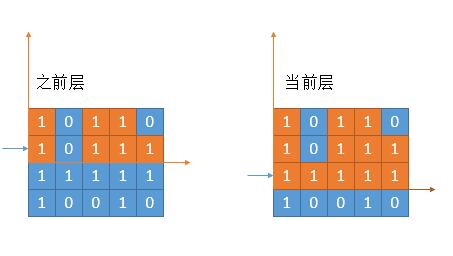
然而事实是残酷的，一定会有 0 的出现。

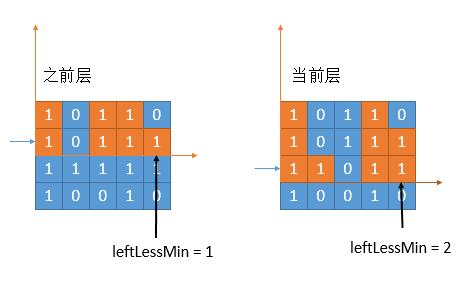
我们考虑最后一个柱子的更新。上一层的 leftLessMin = 1，也就是蓝色 0 的位置是第一个比它低的柱子。但是在当前层，由于中间出现了 0。所以不再是之前的 leftLessMin ，而是和上次出现 0 的位置进行比较（因为 0 一定比当前柱子小），谁的下标大，更接近当前柱子，就选择谁。上图中出现 0 的位置是 2，之前的 leftLessMin 是 1，选一个较大的，那就是 2 了。

public int maximalRectangle4(char[][] matrix) {
    if (matrix.length == 0) {
        return 0;
    }
    int maxArea = 0;
    int cols = matrix[0].length;
    int[] leftLessMin = new int[cols];
    int[] rightLessMin = new int[cols];
    Arrays.fill(leftLessMin, -1); //初始化为 -1，也就是最左边
    Arrays.fill(rightLessMin, cols); //初始化为 cols，也就是最右边
    int[] heights = new int[cols];
    for (int row = 0; row < matrix.length; row++) {
        //更新所有高度
        for (int col = 0; col < cols; col++) {
            if (matrix[row][col] == '1') {
                heights[col] += 1;
            } else {
                heights[col] = 0;
            }
        }
        //更新所有leftLessMin
        int boundary = -1; //记录上次出现 0 的位置
        for (int col = 0; col < cols; col++) {
            if (matrix[row][col] == '1') {
                //和上次出现 0 的位置比较
                leftLessMin[col] = Math.max(leftLessMin[col], boundary);
            } else {
                //当前是 0 代表当前高度是 0，所以初始化为 -1，防止对下次循环的影响
                leftLessMin[col] = -1; 
                //更新 0 的位置
                boundary = col;
            }
        }
        //右边同理
        boundary = cols;
        for (int col = cols - 1; col >= 0; col--) {
            if (matrix[row][col] == '1') {
                rightLessMin[col] = Math.min(rightLessMin[col], boundary);
            } else {
                rightLessMin[col] = cols;
                boundary = col;
            }
        }

        //更新所有面积
        for (int col = cols - 1; col >= 0; col--) {
            int area = (rightLessMin[col] - leftLessMin[col] - 1) * heights[col];
            maxArea = Math.max(area, maxArea);
        }

    }
    return maxArea;

}

时间复杂度：O（mn）。

空间复杂度：O（n）。