网友：感谢华为救了我的下半生。

news2024/9/21 16:19:49

(关注数据结构和算法，了解更多新知识)

最近一位网友发视频称，华为Mate60 Pro帮他挡了子弹。视频配文：“一场意外，没有这个手机隔挡，下半生我可能就在轮椅上度过了！”视频中，手机摄像头右侧被击中，该网友还晒出了自己大腿中枪受伤的照片。

在该视频的下面其中一位网友评论说：本以为是闹着玩的，直到看见了他的IP。该IP显示的是云南，应该是处于云南和果敢的交界处。

其他网友说：打中的应该是流弹，反弹后的子弹或者碎片，如果正面直接挡子弹，在加几台手机都不够。我觉得这个才是最真实的，应该是流弹擦伤，幸亏兜里装个手机挡了一下，要不然会更加严重，搞不好下半生就变成下半身了。

--------------下面是今天的算法题--------------

我们来看一道华为的面试题，这题是LeetCode的第221题：最大正方形。一网友在华为的面试中遇到这题，我们来看下。

问题描述

来源：LeetCode第221题

难度：中等

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例1：

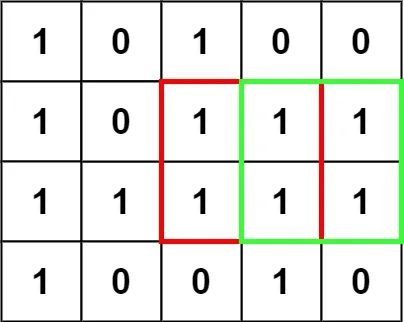
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]

输出：4

示例2：

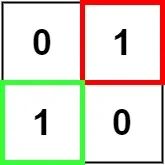
输入：matrix = [["0","1"],["1","0"]]

输出：1

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'

问题分析

这题让计算最大正方形面积，只需要找到最大正方形的边长就可以计算面积了。

可以使用动态规划解决，定义二维数组dp[m][n]，其中dp[i][j]表示在矩阵中以坐标[i,j]为右下角的最大正方形边长。如果想求dp[i][j]，需要判断矩阵中matrix[i][j]的值。

1，如果matrix[i][j]是0就没法构成正方形，所以dp[i][j]=0。

2，如果matrix[i][j]是1，说明可以构成一个正方形，并且这个正方形的边长最小是1。

2.1，如果求最大值，还需要判断他左上角的值dp[i-1][j-1]，如果dp[i-1][j-1]是0，那么以坐标[i,j]为右下角的最大正方形边长就是1，如下图所示

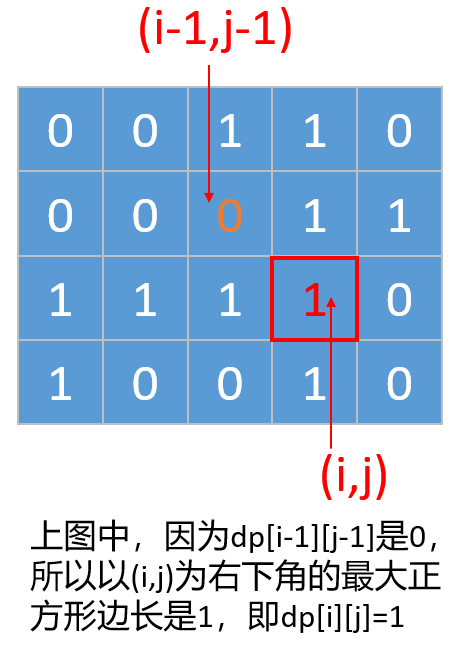
2.2，如果左上角的值dp[i-1][j-1]不是0，那么以坐标[i,j]为右下角有可能可以构成一个更大的正方形。为啥说是有可能，因为如果要确定他能不能构成一个更大的正方形，还要往他的上边和左边找，看下下面的图。

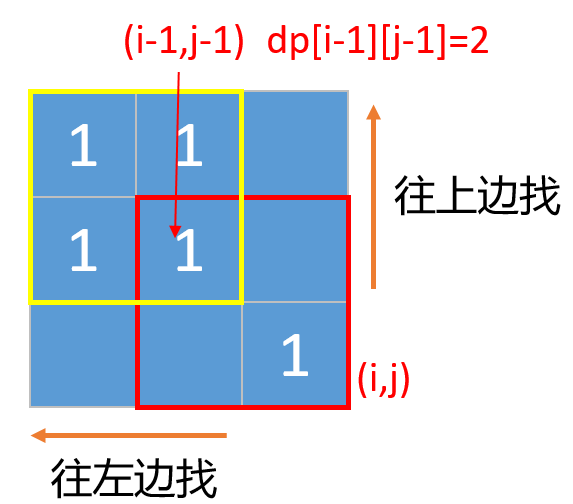
有可能是下面这种情况，就是左边或者上边的某一个高度小于dp[i-1][j-1]的值，要想构成最大的正方形我们只能取最小的。

也有可能是下面这种，就是左边和上边的高度都不小于dp[i-1][j-1]的值。

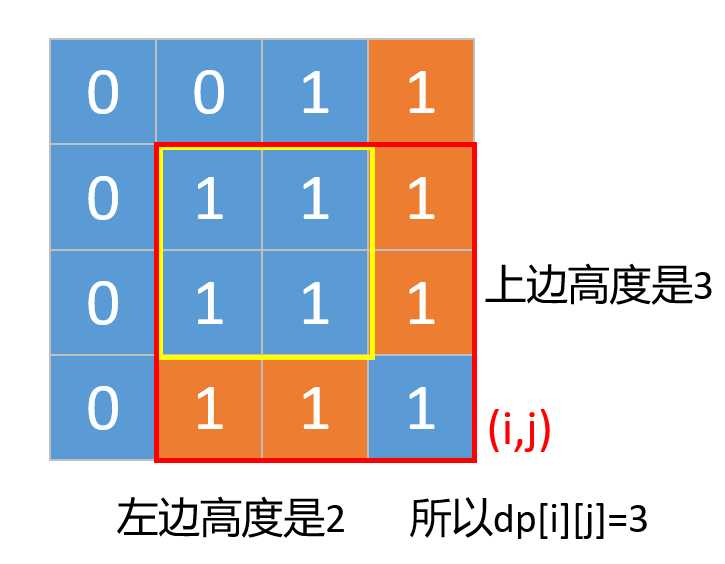
所以我们可以得出结论，如果matrix[i,j]是1，那么以他为右下角的最大正方形边长是min(dp[i-1][j-1]，dp[i-1][j]，dp[i][j-1])+1；

所以我们可以找出递推公式

如果matrix[i,j]为0，则dp[i][j]=0;

如果matrix[i,j]为1，则dp[i][j]=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;

JAVA：

public int maximalSquare(char[][] matrix) {
    // 二维矩阵的宽和高
    int m = matrix.length;
    int n = matrix[0].length;
    int[][] dp = new int[m + 1][n + 1];
    int maxSide = 0;// 最大正方形的宽
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (matrix[i - 1][j - 1] == '1') {
                // 递推公式
                dp[i][j] = Math.min(dp[i - 1][j],
                        Math.min(dp[i - 1][j - 1], dp[i][j - 1])) + 1;
                // 记录最大的边长
                maxSide = Math.max(maxSide, dp[i][j]);
            }
        }
    }
    return maxSide * maxSide; // 返回正方形的面积
}

C++：

public:
    int maximalSquare(vector<vector<char>> &matrix) {
        // 二维矩阵的宽和高
        int m = matrix.size();
        int n = matrix[0].size();
        vector<vector<int>> dp(m + 1, vector(n + 1, 0));
        int maxSide = 0;// 最大正方形的宽
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (matrix[i - 1][j - 1] == '1') {
                    // 递推公式
                    dp[i][j] = min(dp[i - 1][j],
                                   min(dp[i - 1][j - 1], dp[i][j - 1])) + 1;
                    // 记录最大的边长
                    maxSide = max(maxSide, dp[i][j]);
                }
            }
        }
        return maxSide * maxSide; // 返回正方形的面积
    }

C：

#define min(a, b) (((a) < (b)) ? (a) : (b))
#define max(a, b) (((a) > (b)) ? (a) : (b))

int maximalSquare(char **matrix, int matrixSize, int *matrixColSize) {
    // 二维矩阵的宽和高
    int dp[matrixSize + 1][*matrixColSize + 1];
    memset(dp, 0, sizeof dp);
    int maxSide = 0;// 最大正方形的宽
    for (int i = 1; i <= matrixSize; i++) {
        for (int j = 1; j <= *matrixColSize; j++) {
            if (matrix[i - 1][j - 1] == '1') {
                // 递推公式
                dp[i][j] = min(dp[i - 1][j],
                               min(dp[i - 1][j - 1], dp[i][j - 1])) + 1;
                // 记录最大的边长
                maxSide = max(maxSide, dp[i][j]);
            }
        }
    }
    return maxSide * maxSide; // 返回正方形的面积
}

Python：

def maximalSquare(self, matrix: List[List[str]]) -> int:
    # 二维矩阵的宽和高
    m, n = len(matrix), len(matrix[0])
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    maxSide = 0  # 最大正方形的宽
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if matrix[i - 1][j - 1] == '1':
                # 递推公式
                dp[i][j] = min(dp[i - 1][j], dp[i - 1][j - 1], dp[i][j - 1]) + 1
                # 记录最大的边长
                maxSide = max(maxSide, dp[i][j])
    return maxSide * maxSide  # 返回正方形的面积