目录
1、redis之布隆过滤
2、布隆过滤器原理
3、布隆过滤器使用步骤
初始化bitmap
添加占坑位
判断是否存在圜
1、redis之布隆过滤
布隆过滤:有一个初值都为0的bit数组和多个哈希函数构成,用来快速判断集合中是否存在某个元素。目的:减少内存使用。使用方式:不保存数据信息,只是在内存中做一个是否存在的标记flag
应用场景:布隆过滤器常用于需要快速判断某个元素是否存在的场景,如缓存系统、拼写检查器、垃圾邮件过滤等。
特点:可以高效的插入和查询,占用空间少,布隆过滤器可以添加元素,但是不能删除元素,由于
涉及hashcode判断依据,删掉元素会导致误判率增加。
如果一个元素判断结果:存在时,元素不一定存在,但是判断结果为不存在时,则一定不存在。

2、布隆过滤器原理
布隆过滤器(Bloom Filter)是一种专门用来解决去重问题的高级数据结构。实质就是一个大型位数组和几个不同的无偏hash函数(无偏表示分布均匀)。由一个初值都为零的bit数组和多个个哈希函数构成,用来快速判断某个数据是否存在。
添加key时
- 使用多个hash函数对key进行hash运算得到一个整数索引值,对位数组长度进行取模运算得到一个位置,每个hash函数都会得到一个不同的位置,将这几个位置都置1就完成了add操作。
查询key时
- 只要有其中一位是零就表示这个key不存在,但如果都是1,则不一定存在对应的key。
hash冲突导致数据不精准
当有变量被加入集合时,通过N个映射函数将这个变量映射成位图中的N个点,把它们置为1(假定有两个变量都通过3个映射函数)。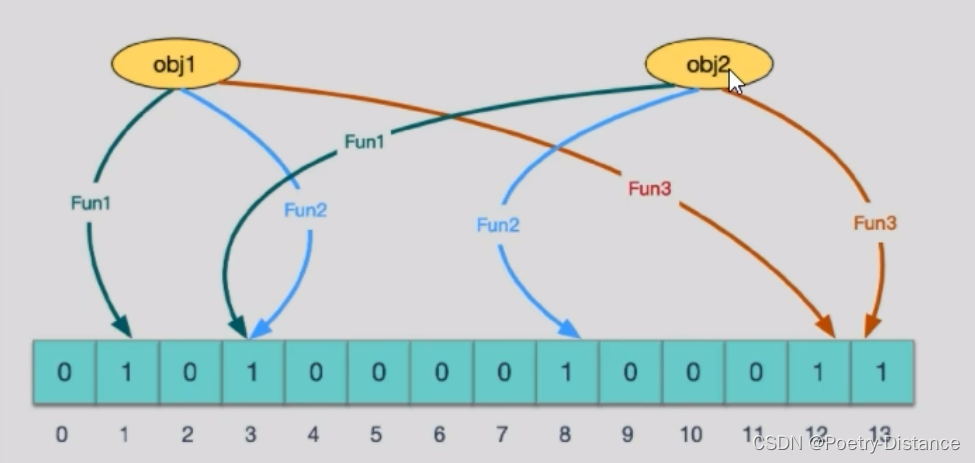
查询某个变量的时候我们只要看看这些点是不是都是1,就可以大概率知道集合中有没有它了
如果这些点,有任何一个为零则被查询变量一定不在,如果都是1,则被查询变量很可能存在,
为什么说是可能存在,而不是一定存在呢?那是因为映射函数本身就是散列函数,散列函数是会有碰撞的。
哈希函数的概念:将任意大小的输入数据转换成特定大小的输出数据的函数,转换后的数据称为哈希值或哈希编码,也叫散列值。

如果两个散列值是不相同的(根据同一函数)那么这两个散列值的原始输入也是不相同的,这个特性是散列函数具有确定性的结果,具有这种性质的散列函数称为单向散列函数。
散列函数的输入和输出不是唯一对应关系的,如果两个散列值相同,两个输入值很可能是相同的,但也可能不同,这种情况称为“散列碰撞(collision)”。
用hash表存储大数据量时,空间效率还是很低,当只有一个 hash函数时,还很容易发生哈希碰撞。
演示哈希碰撞
public class HashCodeConflictDemo{
public static void main(String[] args){
System.out.println("Aa".hashCode());
System.out.println("BB".hashCode());
System.out.println("柳柴".hashCode());
System.out.println("柴柕".hashCode());
Set<Integer> hashCodeSet = new HashSet<>();
for (int i = 0; i <200000; i++) {
int hashCode = new Object().hashCode();
if(hashCodeSet.contains(hashCode)) {
System.out.println("出现了重复的hashcode: "+hashCode+"\t 运行到"+i);
break;
}
hashCodeSet.add(hashCode);
}
}
}

3、布隆过滤器使用步骤
初始化bitmap
布隆过滤器本质上是由长度为 m的位向量或位列表(仅包含0或1位值的列表)组成,最初所有的值均设置为0
添加占坑位
当我们向布隆过滤器中添加数据时,为了尽量地址不冲突,会使用多个hash函数对 key进行运算,算得一个下标索引值,然后对位数组长度进行取模运算得到一个位置,每个 hash函数都会算得一个不同的位置。再把位数组的这几个位置都置为1就完成了add 操作。
例如,我们添加一个字符串wmyskxz,对字符串进行多次hash(key)→取模运行→得到坑位

判断是否存在圜
向布隆过滤器查询某个key是否存在时,先把这个key通过相同的多个hash函数进行运算,查看对应的位置是否都为1,只要有一个位为零,那么说明布隆过滤器中这个key不存在;
如果这几个位置全都是1,那么说明极有可能存在;
因为这些位置的1可能是因为其他的 key存在导致的,也就是前面说过的hash冲突
为什么不能删除
因为布隆过滤器的每一个bit并不是独占的.很有可能多个元素共享了某一位。如果我们直接删除这一位的话,会影响其他的元素。
小结:使用时最好不要让实际元素数量远大于初始化数量,一次给够避免扩容。当实际元素数量超过初始化数量时,应该对布隆过滤器进行重建,重新分配一个size更大的过滤器,再将所有的历史元素批量add进行。