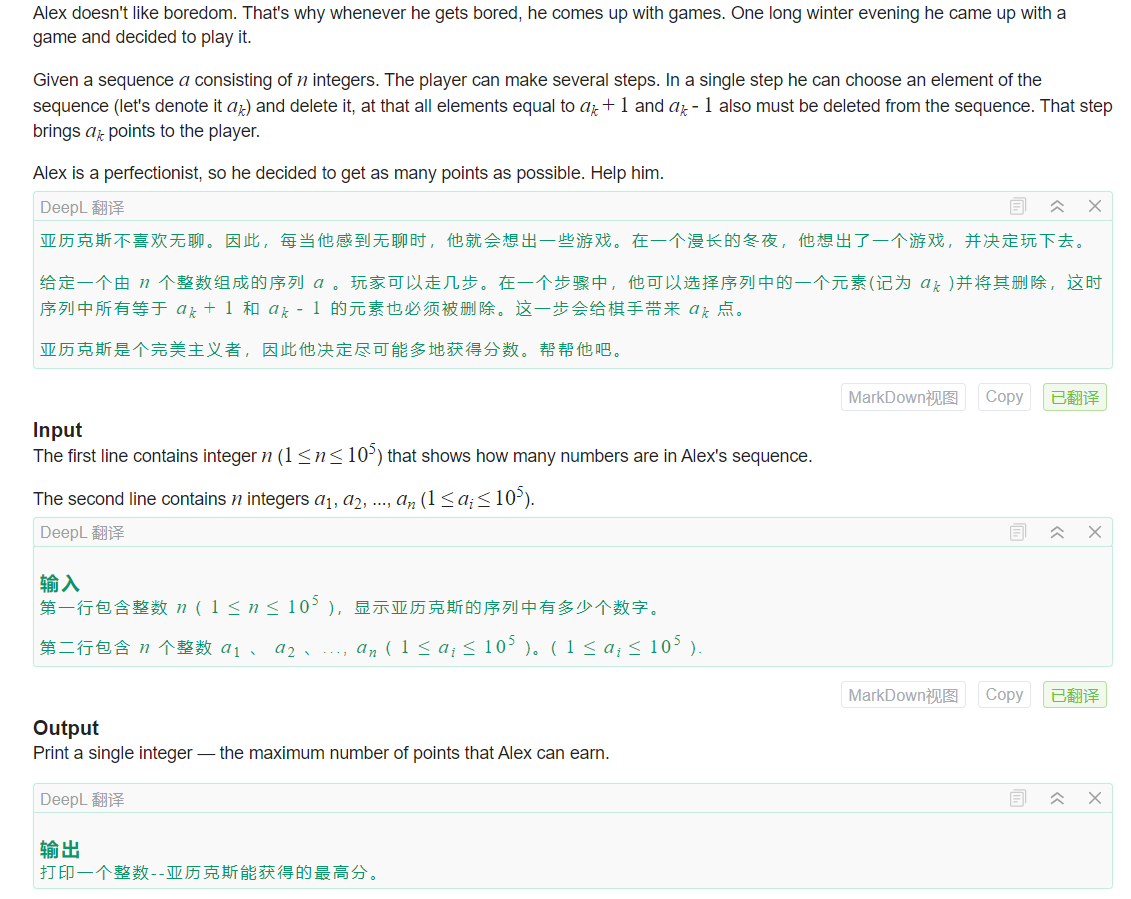
最开始写了一发贪心wa了，然后这种选和不选的组合优化问题，一般是考虑动态规划

$dp[i][0]：$表示第i个数不选的最大值
$dp[i][1]：$表示第i个数选的最大值

考虑转移：
$dp[i][0]=max(dp[i-1][1],dp[i-1][0])$
$dp[i][1]=dp[i-1][1]+a[i]\ast i$
需要将每一个数用一个桶统计次数
因为n比较小。
最后答案在$dp[n][0]和dp[n][1]$两者中取一个最大值即可

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define pll pair<long long, long long>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

const int N=1e6+10,mod=1e9+7;
int dp[N][2];
int a[N];
void solve()
{
	int n;cin>>n;
	int m=0;
	rep(i,1,n){
		int x;cin>>x;
		a[x]++;
		m=max(m,x);
	}	
	
	rep(i,1,m){
		dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
		dp[i][1]=dp[i-1][0]+a[i]*i;
	}
	cout<<max(dp[m][0],dp[m][1])<<endl;	
}

signed main(){
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);
  	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}