一、二分法

二分法查找主要是为了快速查找给定数组内，期待值在数组中的位置（下标）

二分法查找通过对整个数组取中间值，判断期待值所在的范围并缩小范围，每次查找范围折半，直到范围的边界重合，得出期待值的位置，如果找不到返回-1

二分法有一个先决条件是：数组内元素必须是有序的

给定一个包含1，3，5，7，8，9这一个元素的有序数组，求得期待值7所在的位置，下边用绿块表示指针所在位置

若是按照直接遍历的方式，绿块会从数组的第一个下标开始比较，直到7所在的下标得到结果，遍历需要4次，下边演示下二分法的图示

第一次，取值范围为整个数组，取数组长度中间值(0+5)/2取整2作为下标

取中间值初始以数组的第一个下标与最后一个下标相加取中间值，如果不为整，舍去小数部分

比较期待值与下标为2的值大小，发现5<7，7这个值应在中间值的右侧

缩小查找范围为中间值+1与最大下标

第二次，范围缩小为原数组的一半，下标不变，取中间值(3+5)/2=4

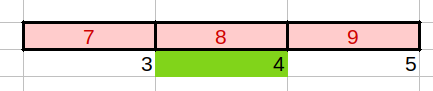
下标4对应的值8，大于7，所以向左取范围最小下标3，最大下标4-1=3

第三次，取中间值(3+3)/2=3，下标3上的值恰好与期待值相等，返回下标3

虽然看起来只少了一次，原因在数组的长度小，另外就是期待值设置的小，

再举个长一点的例子，这里有1-100的数组，100个元素，期待值为100

简单遍历次数最大为元素的个数n次，本例中100次

使用二分查找只需要log2n次，本例中7次！

 代码实现

package binarysearch;
 
/**
 * 二分查找：求得期待值在有序数组中的位置
 * @author hellxz
 */
public class MyBinarySearch {
 
	/**
	 * 二分查找算法实现
	 * @param orderedArray 有序数组
	 * @param expect 期待数值
	 * @return 期待值在数组中的下标，如果期待数值不在数组中，返回-1
	 */
	public static Integer binarySearch(int[] orderedArray, int expect) {
        if(orderedArray.length==0){
            return -1;
        }   
		//low与high构成动态的数组下标范围
		//初始low下标为0，high为数组长度-1
		int low = 0;
		int high = orderedArray.length - 1;
 
		//当数组范围存在时，有两种情况：最小边界值小于最大边界值 或 两个边界值相等；
		//最小边界值不大于最大边界值是有意义的，表示范围的存在，如果范围不存在了，说明数组中无此元素
		while (low <= high) {
			//取两个边界下标的中间下标与中间值，作为下标时会自动取整
			int middle = (low + high) / 2;
			int middleVal = orderedArray[middle];
			//中间值与期待值相等，说明中间值的下标就是我们要找的期待数的下标
			if (middleVal == expect) {
				return middle;
			}
			//中间值小于期待值，我们需要将最小边界下标移到中间下标的下一位
			//此时，最大边界不变，最小边界变大，范围缩小原来一半
			if (middleVal < expect) {
				low = middle + 1;
			}
			//中间值大于期待值，说明最大边界应小于中间下标
			if (middleVal > expect) {
				high = middle - 1;
			}
		}
 
		//循环结束未返回下标说明数组中不存在期待元素，返回-1
		return -1;
	}
 
	public static void main(String[] args) {
		int[] arr = { 2, 4, 5, 6, 10, 18, 19,22, 25, 70};
		int expectVal = 25;
		System.out.printf("当前期待的值为%d，其所在的下标为%d", expectVal, binarySearch(arr, expectVal));
	}
}