第6章 与学习相关的技巧
本章将介绍神经网络的学习中的一些重要观点,主题涉及
寻找最优权重参数的最优化方法、权重参数的初始值、超参数的设定方法
等。此外,为了应对过拟合,本章还将介绍
权值衰减、Dropout等正则化方法,并进行实现
。最后将对近年来众多研究中使用的
Batch Normalization
方法进行简单的介绍。使用本章介绍的方法,可以高效地进行神经网络(深度学习)的学习,提高识别精度。
6.1 参数的更新
神经网络的学习的目的是找到使损失函数的值尽可能小的参数
。这是寻找最优参数的问题,解决这个问题的过程称为
最优化(optimization)
。遗憾的是,神经网络的最优化问题非常难。这是因为参数空间非常复杂,无法轻易找到最优解(无法使用那种通过解数学式一下子就求得最小值的方法)。而且,在深度神经网络中,参数的数量非常庞大,导致最优化问题更加复杂。
在前几章中,为了找到最优参数,我们将参数的梯度(导数)作为了线索。使用参数的梯度,沿梯度方向更新参数,并重复这个步骤多次,从而逐渐靠近最优参数,这个过程称为
随机梯度下降法(stochastic gradient descent),简称SGD
。
SGD
是一个简单的方法,不过比起胡乱地搜索参数空间,也算是“聪明”的方法。但是,根据不同的问题,也存在比
SGD更加聪明的方法。本节我们将指出
SGD
的缺点,并介绍
SGD
以外的其他最优化方法。
6.1.1 探险家的故事
6.1.2 SGD
让大家感受了最优化问题的难度之后,我们再来复习一下
SGD
。用数学式可以将
SGD
写成如下的式(
6
.
1
)。

class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
这里,进行初始化时的参数
lr表示learning rate(学习率)
。这个学习率会保存为实例变量。此外,代码段中还定义了
update(params, grads)
方法,这个方法在
SGD
中会被反复调用。参数
params
和
grads
(与之前的神经网络的实现一样)是字典型变量,按
params['W1']
、
grads['W1']
的形式,分别保存了权重参数和它们的梯度。
使用这个
SGD
类,可以按如下方式进行神经网络的参数的更新(下面的代码是不能实际运行的伪代码)。
network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
...
x_batch, t_batch = get_mini_batch(...) # mini-batch
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params, grads)
...
这里首次出现的变量名
optimizer
表示“进行最优化的人”(翻译为优化器可能更好)的意思,这里
由
SGD
承担这个角色。参数的更新由
optimizer
负责完成。我们在这里需要做的只是将参数和梯度的信息传给
optimizer
。
像这样,通过单独实现进行最优化的类,功能的模块化变得更简单。比如,后面我们马上会实现另一个最优化方法
Momentum
,它同样会实现成拥有
update(params, grads)
这个共同方法的形式。这样一来,只需要将
optimizer = SGD()
这一语句换成
optimizer = Momentum()
,就可以从
SGD
切
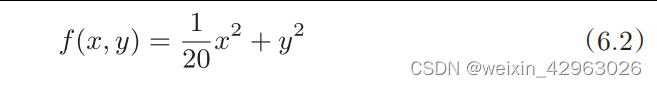
换为
Momentum
。
很多深度学习框架都实现了各种最优化方法,并且提供了可以简单切换这些方法的构造。比如 Lasagne深度学习框架,在
updates.py这个文件中以函数的形式集中实现了最优化方法。用户可以从中选择自己想用的最优化方法。
6.1.3 SGD的缺点
虽然
SGD
简单,并且容易实现,但是在解决某些问题时可能没有效率。这里,在指出
SGD
的缺点之际,我们来思考一下求下面这个函数的最小值的问题。
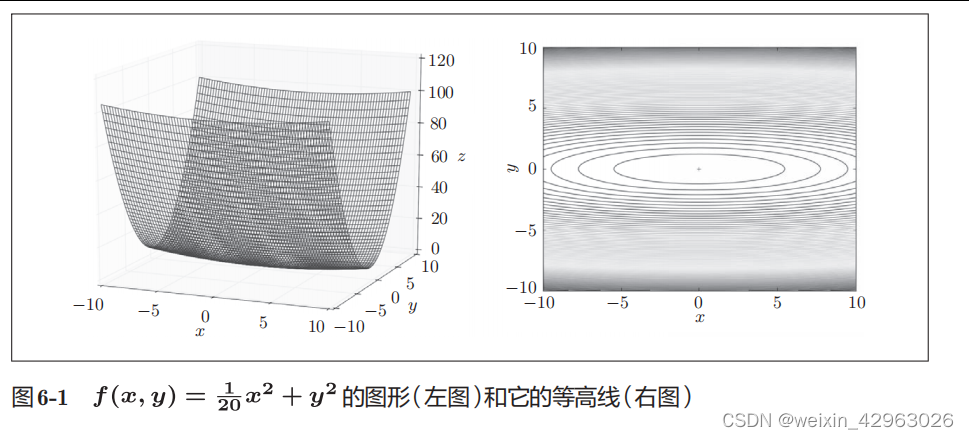
如图
6-1
所示,式(
6
.
2
)表示的函数是向
x
轴方向延伸的“碗”状函数。实际上,式(
6
.
2
)的等高线呈向
x
轴方向延伸的椭圆状。