---

前言

读前须知：
首先我们得确保你已经完全知晓相关的基本的数学知识，其中包括用最小二乘法拟合曲二次曲面，以及曲面的曲率详细求解。若还是没弄清楚，则详细请看下面链接。

【点云、图像】学习中 常见的数学知识及其中的关系与python实战[更新中]（建议从一个标题上从上往下看，比较循序渐进）

补充：曲率：反映曲面在某一点处的弯曲程度，它与该点及其邻近点的位置和法向量有关。

以及一些open3d的常见操作：
爆肝5万字❤️Open3D 点云数据处理基础（Python版）

先上结果:

---

实现思路

不同于常见的缺陷检测，如：划痕或者斑点这些肉眼可见的缺陷，凹凸性缺陷难以肉眼可见甚至得打光照射才能看见凹槽，这里我们使用深度摄像机（普通相机＋深度信息），来采集深度信息。此时我们把图像称为深度图，当然深度图也可以转换为点云。

这里我们仅对点云这种数据进行处理。

要求：对异形曲面微细缺陷识别（我6月份之前要完成的毕设）
这里缺陷主要指凸起和凹槽。

想法1

想法1：如果是一个平面上出现凹槽或凸起的话，首先确立一个由大部分点拟合的平面，然后对不在此平面的点云进行高程分析，以确立凹陷或凸起程度。
（事实上不会很平，于是想法1排除，但可以用来做平面来做一个简单示例）

想法2

想法2：计算点云上每个点的领域曲率来描绘点的弯曲程度。

想法3

想法3：计算点云上每个点的高斯曲率和平均曲率来描绘点的弯曲程度。

补充

机器学习——详解KD-Tree原理

实现

想法1

暂无

想法2

想法2：
在求取完领域曲率的基础上，我们对其曲率的大小进行一个分割，并进行可视化。

这里进一步对这个领域曲率的定义进行详解。
首先，我们已经在这里的实战1了解到了领域曲率的求法。

基于邻域特征点提取和匹配的点云配准_李新春

可是这个定义我只在其他的博客中和下面这篇论文中找到定义，并无在wiki百科中找到相关阐述。

找了半天后依然无法解释其中原因，于是在参考了下面两篇博文后
如何理解矩阵特征值？
特征值的最大值与最小值
想出了这么一个合理的解释：
1、这个曲率定义的优点是，它不依赖于法向量的方向，而且它的值域是 [0, 1/3]，这使得它比较容易进行归一化和可视化。

2、那么，为什么用最小的特征值除以特征值和，而不是用最大的特征值除以特征值和呢？

这是因为最小的特征值对应的特征向量是曲面的法向量，而最大的特征值对应的特征向量是曲面的主方向。

如果用最大的特征值除以特征值和，那么曲率的值就会与曲面的主方向的弯曲程度成正比，而与曲面的法向方向的弯曲程度无关。这样就会忽略掉曲面的凹凸变化，导致曲率的计算不准确。

如果用最小的特征值除以特征值和，那么曲率的值就会与曲面的法向方向的弯曲程度成正比，而与曲面的主方向的弯曲程度无关。这样就可以反映出曲面的凹凸变化，提高曲率的计算精度。

因此，用最小的特征值除以特征值和，而不是用最大的特征值除以特征值和，是为了更好地描述曲面的局部形状，而不是曲面的整体方向。

于是我们就可以坦然用这个定义来求取了。

代码

怕点云太多算不过来，首先对例子中的兔子点云进行了一个下采样。（如何获取兔子点云到时候再出教程）

import open3d as o3d
import numpy as np

def pca_compute(data, sort=True): #1、主成分分析
    average_data = np.mean(data, axis=0) # 求每一列的平均值，即求各个特征的平均值
    decentration_matrix = data - average_data  # 去中心化矩阵
 
    H = np.dot(decentration_matrix.T, decentration_matrix)  # 求协方差矩阵 #协方差是衡量两个变量关系的统计量，协方差为正表示两个变量正相关，为负表示两个变量负相关
    eigenvectors, eigenvalues, eigenvectors_T = np.linalg.svd(H) # 求特征值与特征向量 #H = UΣV^T #输出列向量、对角矩阵、行向量
    if sort:
        sort = eigenvalues.argsort()[::-1] # 从大到小排序 .argsort()是升序排序，[::-1]是将数组反转，实现降序排序
        eigenvalues = eigenvalues[sort] # 特征值  ## 使用索引来获取排序后的数组
    return eigenvalues
 
def caculate_surface_curvature(radius,pcd):#2、计算点云的表面曲率
    cloud = pcd
    points = np.asarray(cloud.points) #点云转换为数组 点云数组形式为[[x1,y1,z1],[x2,y2,z2],...]
    kdtree = o3d.geometry.KDTreeFlann(cloud) #建立KDTree
    num_points = len(cloud.points) #点云中点的个数
    curvature = []  # 储存表面曲率
    for i in range(num_points):
        k, idx, _ = kdtree.search_radius_vector_3d(cloud.points[i], radius) #返回邻域点的个数和索引
        neighbors = points[idx] #数组形式为[[x1,y1,z1],[x2,y2,z2],...]
        w = pca_compute(neighbors)#调用第1步  #由降序排序，w[2]为最小特征值  #np.zeros_like(w[2])生成与w[2]相同形状的全0数组
        delt = np.divide(w[2], np.sum(w)) #根据公式求取领域曲率
        curvature.append(delt)
    curvature = np.array(curvature, dtype=np.float64)
    return curvature
 
def curvature_normal():#3、曲率归一化 从0-1/3归到0-1之间
    curvature = caculate_surface_curvature(radius,pcd) #调用第2步
    c_max = max(curvature)
    c_min = min(curvature)
    cur_normal = [(float(i) - c_min) / (c_max - c_min) for i in curvature] 
    return cur_normal
 
def draw(cur_max,cur_min,pcd):#4、绘图
    cur_normal = curvature_normal()#调用第3步
    pcd.paint_uniform_color([0.5,0.5,0.5]) #初始化所有颜色为灰色
    for i in range(len(cur_normal)):
        if 0 < cur_normal[i] <= cur_min: #归一化后的曲率
            np.asarray(pcd.colors)[i] = [1, 0, 0]#红
        elif cur_min < cur_normal[i] <= cur_max:
            np.asarray(pcd.colors)[i] = [0, 1, 0]#绿
        elif cur_max < cur_normal[i] <= 1: 
            np.asarray(pcd.colors)[i] = [0, 0, 1]#蓝
 
    # 可视化
    o3d.visualization.draw_geometries([pcd])

cur_max = 0.7 
cur_min = 0.3 #曲率分割基准
radius = 0.05
voxel_size = 0.01 #越小密度越大
pcd = o3d.io.read_point_cloud("bunny.pcd")
print(pcd)
pcd = pcd.voxel_down_sample(voxel_size) #下采样
draw(cur_max,cur_min,pcd)
 

结果：

这个长度，宽度报错可以不管，有点子强迫症的可以在可视化改成：

    o3d.visualization.draw_geometries([pcd],window_name="可视化原始点云",
                                      width=800, height=800, left=50, top=50,
                                      mesh_show_back_face=False)

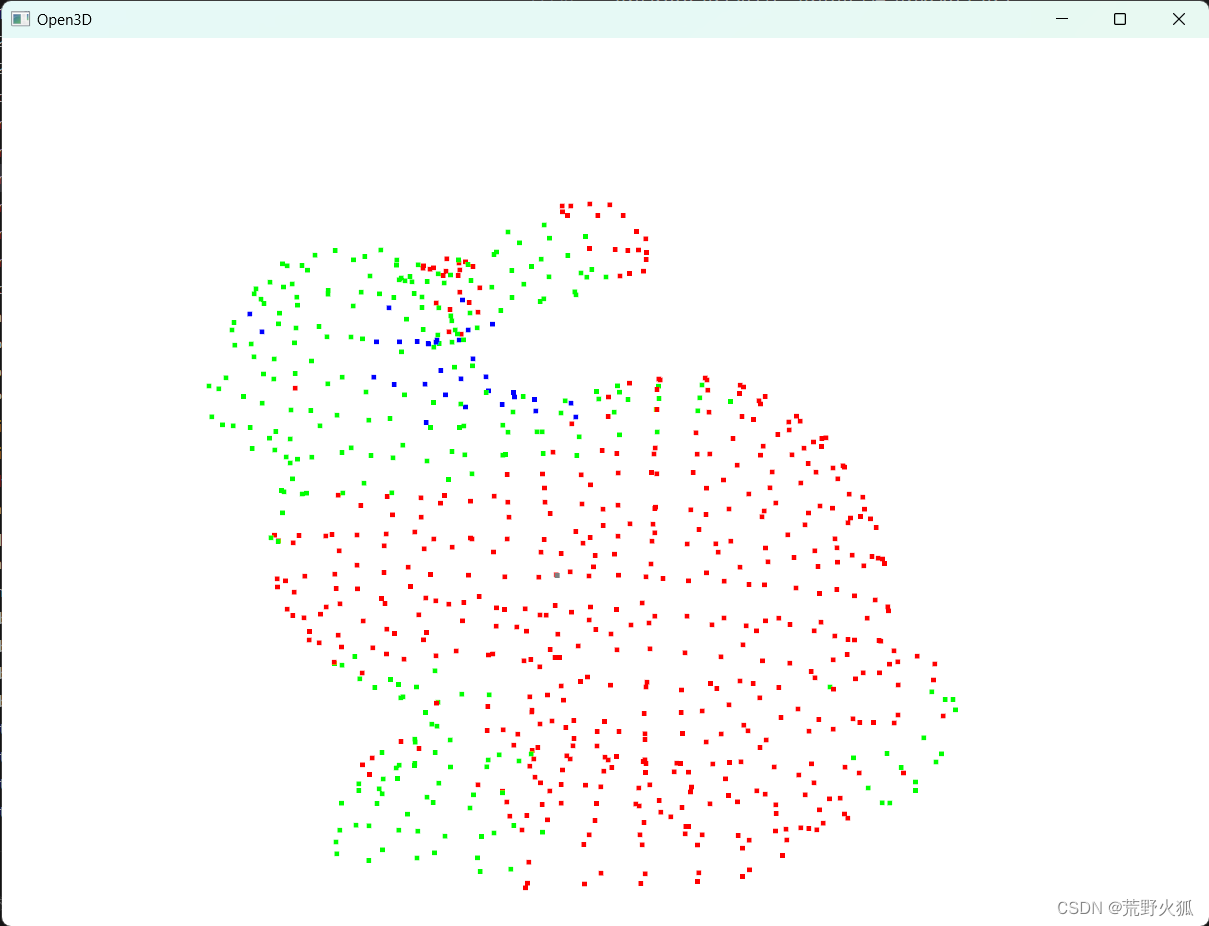
红色为曲率较低，绿色曲率中等，蓝色曲率较高。
发现效果上不太行，红色一些部分看着曲率也很高，甚至还出现了一个初始化时候的灰点，可能求邻近点的时候没取到？不曾得知。

想法3

首先我们在这里的高斯曲率和平均曲率求解有了一些认识。
附一张图：

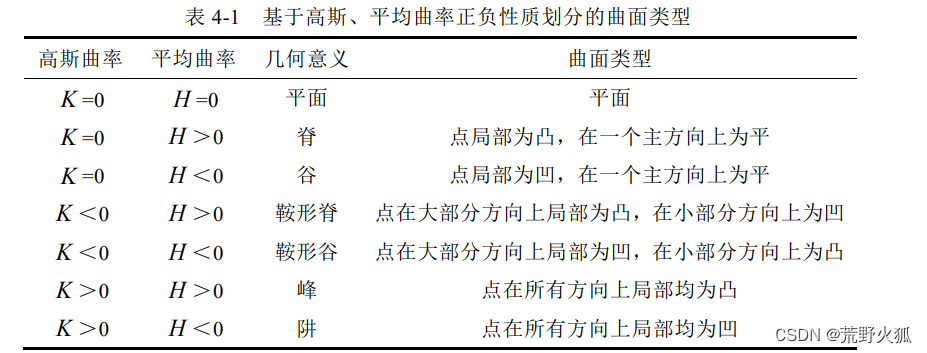
代码

import open3d as o3d
import numpy as np
from scipy.optimize import curve_fit

voxel_size = 0.01 #越小密度越大
radius = 0.07
pcd = o3d.io.read_point_cloud("bunny.pcd")
pcd = pcd.voxel_down_sample(voxel_size) #下采样
cloud = pcd
points = np.asarray(cloud.points) #点云转换为数组 点云数组形式为[[x1,y1,z1],[x2,y2,z2],...]
kdtree = o3d.geometry.KDTreeFlann(cloud) #建立KDTree
num_points = len(cloud.points) #点云中点的个数
pcd.paint_uniform_color([1, 0, 0])  # 初始化所有颜色为红色
# 定义非线性函数，这里假设是一个二次曲面
def func(x, a, b, c, d, e, f):
    return a * x[0]**2 + b * x[1]**2 + c * x[0] * x[1] + d * x[0] + e * x[1] + f
def f(x, y):
    return popt[0]*x**2 +popt[1]*y**2 +popt[2]* x*y +popt[3]*x + popt[4]*y +popt[5]
# 定义曲面的梯度函数，即一阶偏导数
def gradient(f, x, y):
    # 使用中心差分法近似求导  #参考https://cloud.tencent.com/developer/article/1685164
    h = 1e-6 # 差分步长，可以根据精度要求调整
    df_dx = (f(x + h, y) - f(x - h, y)) / (2 * h) # 对x求偏导
    df_dy = (f(x, y + h) - f(x, y - h)) / (2 * h) # 对y求偏导
    return df_dx, df_dy
# 定义曲面的曲率函数，即二阶偏导数
def curvature(f, x, y):
    # 使用中心差分法近似求导
    h = 1e-6 # 差分步长，可以根据精度要求调整
    d2f_dx2 = (f(x + h, y) - 2 * f(x, y) + f(x - h, y)) / (h ** 2) # 对x求二阶偏导
    d2f_dy2 = (f(x, y + h) - 2 * f(x, y) + f(x, y - h)) / (h ** 2) # 对y求二阶偏导
    d2f_dxdy = (f(x + h, y + h) - f(x + h, y - h) - f(x - h, y + h) + f(x - h, y - h)) / (4 * h ** 2) # 对xy求混合偏导
    # 根据公式计算高斯曲率K和平均曲率H
    df_dx, df_dy = gradient(f, x, y) # 调用梯度函数求一阶偏导
    E = 1 + df_dx ** 2
    F = df_dx * df_dy
    G = 1 + df_dy ** 2
    L = d2f_dx2 / np.sqrt(1 + df_dx ** 2 + df_dy ** 2) #np.sqrt()表示开方
    M = d2f_dxdy / np.sqrt(1 + df_dx ** 2 + df_dy ** 2)
    N = d2f_dy2 / np.sqrt(1 + df_dx ** 2 + df_dy ** 2)
    K = (L * N - M ** 2) / (E * G - F ** 2) # 高斯曲率
    H = (E * N + G * L - 2 * F * M) / (2 * (E * G - F ** 2)) # 平均曲率
    return K, H

curvatures = []  
for i in range(num_points):
    k, idx, _ = kdtree.search_radius_vector_3d(cloud.points[i], radius) #返回邻域点的个数和索引
    neighbors = points[idx] #数组形式为[[x1,y1,z1],[x2,y2,z2],...]
    #print(k)
    Y = neighbors[:, 2] # 因变量
    X = neighbors[:, [0,1]] # 自变量 [[2,3],[1,1],[8,9],[11,12],[4,5],[8,9]] 6*2
    popt, pcov = curve_fit(func, xdata=X.T,ydata= Y)
    x = cloud.points[i][0] # 某一点的x坐标
    y = cloud.points[i][1] # 某一点的y坐标
    K, H = curvature(f, x, y) # 计算该点的曲率
    curvatures.append([K,H])

print(curvatures)
for i in range(len(curvatures)):
    if -0.05<curvatures[i][0] < 0.05 and -0.05<curvatures[i][1] <0.05: #平坦
        np.asarray(pcd.colors)[i] = [0, 0, 0]#黑
    elif -0.05<curvatures[i][0] < 0.05 and curvatures[i][1] >0.05:  #凸
        np.asarray(pcd.colors)[i] = [1, 0, 0]#红
    elif -0.05<curvatures[i][0] < 0.05 and -0.05<curvatures[i][1] <0.05: #凹
        np.asarray(pcd.colors)[i] = [0, 1, 0]#绿
    elif curvatures[i][0] < -0.05 and curvatures[i][1] >0.05: #鞍形脊 大部分凸，少部分凹
        np.asarray(pcd.colors)[i] = [0, 0, 1]#蓝
    elif curvatures[i][0] < -0.05 and curvatures[i][1] <-0.05: #鞍形谷 大部分凹，少部分凸
        np.asarray(pcd.colors)[i] = [0, 1, 1]#青
    elif curvatures[i][0] > 0.05 and curvatures[i][1] >0.05: #峰 
        np.asarray(pcd.colors)[i] = [1, 0, 1]#紫
    elif curvatures[i][0] > 0.05 and curvatures[i][1] <-0.05: #阱
        np.asarray(pcd.colors)[i] = [1, 1, 0]#黄


#显示点云
o3d.visualization.draw_geometries([pcd])

结果：

结果出奇的好，每个点都进行了划分，比想法1好太多了。这里暂时用兔子点云测试，到时候创造一些平面点云再来测试一下。

---

总结

学习东西都不是一蹴而就的，果然还是得一步一步脚踏实地地学才学的明白。chatgpt是个好东西，只有你也会点东西时，它才会回答的正确，不能轻信之。

未完成：
ps:1、兔子点云pcd读取
2、创建平面点云
3、返回面积、深度信息