目录
1.课题概述
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
1.课题概述
电力系统可靠性是指电力系统按可接受的质量标准和所需数量不间断地向电力用户供应电力和电能量的能力的量度,包括充裕度和安全性两个方面。发电系统可靠性是指统一并网的全部发电机组按可接受标准及期望数量满足电力系统的电力和电能量需求的能力的量度。发电系统可靠性指标可以分为确定性和概率性两类。过去曾广泛应用确定性可靠性指标来指导电力系统规划和运行,如百分数备用法和偶然故障备用法。目前已逐渐被概率性可靠性指标所代替。
概率法常用的可靠性指标有:电力不足概率(Loss of Load Probability, LOLP)和期望缺供电量(Expected Demand Not Served, EDNS)是评估电力系统可靠性的两个重要指标。通过随机法和蒙特卡洛法分别对这两个指标进行仿真分析。
2.系统仿真结果


从仿真可以看到,对于电力不足概率指标LOLP,LOLP值的可能性随着LOLP值得变大而下降,这是因为在模拟元件失效过程中,由于元件失效而导致的电力不足的可能性会出现,但是其大概率的电力不足出现概率较低,而小概率的电力不足情况出现概率较大。
对于停电功率期望值指标EDNS,EDNS值发生可能性的随着EDNS值得变大而下降,即在实际过程中,随着元件失效而发生停电的期望值,其大概率的停电功率出现概率较低,而小概率的停电功率情况出现概率较大。
3.核心程序与模型
版本:MATLAB2022a
.....................................................................
while (Flag == 1)
TTT = TTT + 1;
%断开选定的线路
if TTT == 1
BRANCHo(Cut_info,3:end) = 0;
All_Del_Point= [All_Del_Point;Cut_info'];
else
%断开相邻的线路
Inders1 = find(BRANCHo(:,1) == Cut_info(1));
Inders2 = find(BRANCHo(:,1) == Cut_info(2));
Inders3 = find(BRANCHo(:,2) == Cut_info(1));
Inders4 = find(BRANCHo(:,2) == Cut_info(2));
Inders = unique([Inders1;Inders2;Inders3;Inders4]);
%随机选择
tmpsss = randperm(length(Inders));
Inders_sel = Inders(tmpsss(1));
BRANCHo(Inders_sel,3:end) = 0;
All_Del_Point= [All_Del_Point;Inders_sel];
end
%根据信息节点的Pdi和Pmi进行失去控制
for i1 = 1:N-1
P1 = rand(1);
P2 = rand(1);
if P1 <= Pdi(i1) | (P1 > Pdi(i1) & P2 <= Pmi)
%调度中心认为线路处理初始状态
BRANCHo(i1,3:end) = 0;
All_Del_Point= [All_Del_Point;i1];
end
end
%对此时的电器网络进行计算潮流
Ak = func_Admittance_matrix(BUSo,BRANCHo);
F = Ak * Pp;
%判断是否越限
for jjj = 1:length(F)
if (abs(F(jjj))) <= (abs(Fmax(jjj)))
%没有越限,则进行步骤5
P = rand();
if P <= PH
Flag = 1;%被选中,则继续步骤2,即重新循环
else
Flag = 0;%未被选中,则继续步骤6,跳出循环
end
else
%有越限,则进行步骤3
%先进行LP优化,这里使用PSO进行优化
[V_score2,PP] = func_pso_calculate_min(Bus_Num,15,Pp);
%再计算潮流
Ak = func_Admittance_matrix(BUSo,BRANCHo);
F = Ak*(1+g)*PP;
if sum(abs(F)) > sum(abs(Fmax))
Flag = 1;
else
%没有越限,则进行步骤5
P = rand();
if P <= PH
Flag = 1;%被选中,则继续步骤2,即重新循环
else
Flag = 0;%未被选中,则继续步骤6,跳出循环
end
end
end
end
end
All_Del_Point = unique(All_Del_Point);
LL = length(Fo);
Fedns = zeros(LL,1);
%对于断掉的点取1,其余取0.
Fedns(All_Del_Point) = 1;
deltaP = abs(Fo-F);
E1(m) = sum(Fedns.*deltaP)/LL;
NUMSS(:,m) = NUMS;
[cdf,PAPR] = ecdf(E1);
EDNS = E1;
%%
figure;
semilogy(100*PAPR(1:end-5),1-cdf(1:end-5),'b-o','LineWidth',1);
xlabel('edns');
ylabel('The cumulative probability of failure probability');
if NUM_Delete == 1
save attack41.mat PAPR cdf EDNS NUMSS
end
if NUM_Delete == 2
save attack42.mat PAPR cdf EDNS NUMSS
end
02_027m4.系统原理简介
基于蒙特卡洛的仿真思想,并根据每次产生的随机数种子,进行随机的失效模拟,元件失效过程使用马尔科夫过程建模产生。首先随机模拟一个元件失效的情况,对一个元件失效以及对应的连锁故障情况进行仿真分析。然后随机模拟二个元件失效的情况,对二个元件失效以及对应的连锁故障情况进行仿真分析。而对于三个甚至更多元件失效的情况,本文不做考虑,这是因为当出现三个或者更多的元件失效的情况,整个电力系统网络基本会发生大规模崩溃的情况,在这种情况下做可靠性评估没有实际的价值,故不做这方面的研究。
在本课题中,使用IEEE24-RTS电力网络系统作为案例进行分析
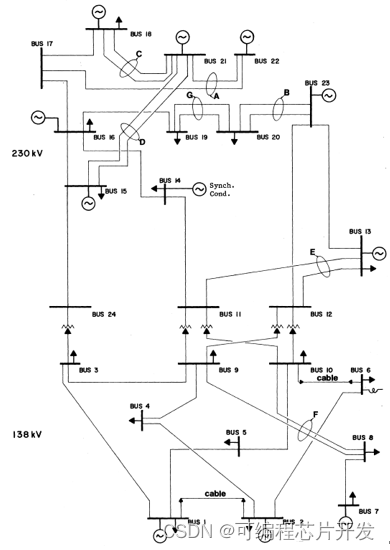
这里采用的仿真步骤如下:
由于我们需要考虑随机断开一条线路或者两条线路的系统的稳定性分析,因此,我们主要通过随机循环的思想,每次循环随机的断开线路,然后分析断开这条线路对系统造成的影响进行仿真分析。
一般情况下,对系统稳定性评估的分析方法主要是分析断开后故障网络的是否正常工作(即分析其是否崩溃)
通常,当断开一条线路的时候,往往会由于该线路的断开而导致其他的线路的连锁故障,从而导致整个系统的影响,但是这种连锁的情况在概率统计中,并不是必然事件,而是随机事件,因此,这里我们设计如下的故障及稳定性分析方法:
第一:首先随机的移除信息网络的信息节点,并计算对应的信息节点的传输信息时的延迟概率P。
第二:随机的选择故障线路,并断开该线路,并更新响应的网络参数;
第三:根据网络参数,通过直流法进行最优潮流的计算(DC OPF),并判断潮流是否存在越限,如果存在越限,则通过LP优化算法进行第四步操作,如果没有越限,则进行第五步操作。
第四:当存在越限的时候,那么基于随机的概率,并采用轮盘赌算法选择随机跳开的线路,并进行再次转入步骤二的操作。
第五:当不存在越限的时候,那么通过一个随机的小概率Ph选择需要跳开的线路,如果存在线路被选择,那么进入步骤二开始操作,否则进入步骤六。
第六:本次蒙特卡洛循环结束,进入下一次循环。
5.完整工程文件
v