LeetCode1365之切披萨的方案数(相关话题：二维前缀和,动态规划)

news2024/11/15 15:37:54

题目描述

给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： 'A' （表示苹果）和 '.' （表示空白格子）。你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含至少一个苹果的切披萨方案数。由于答案可能是个很大的数字，请你返回它对 10^9 + 7 取余的结果。

示例 1：

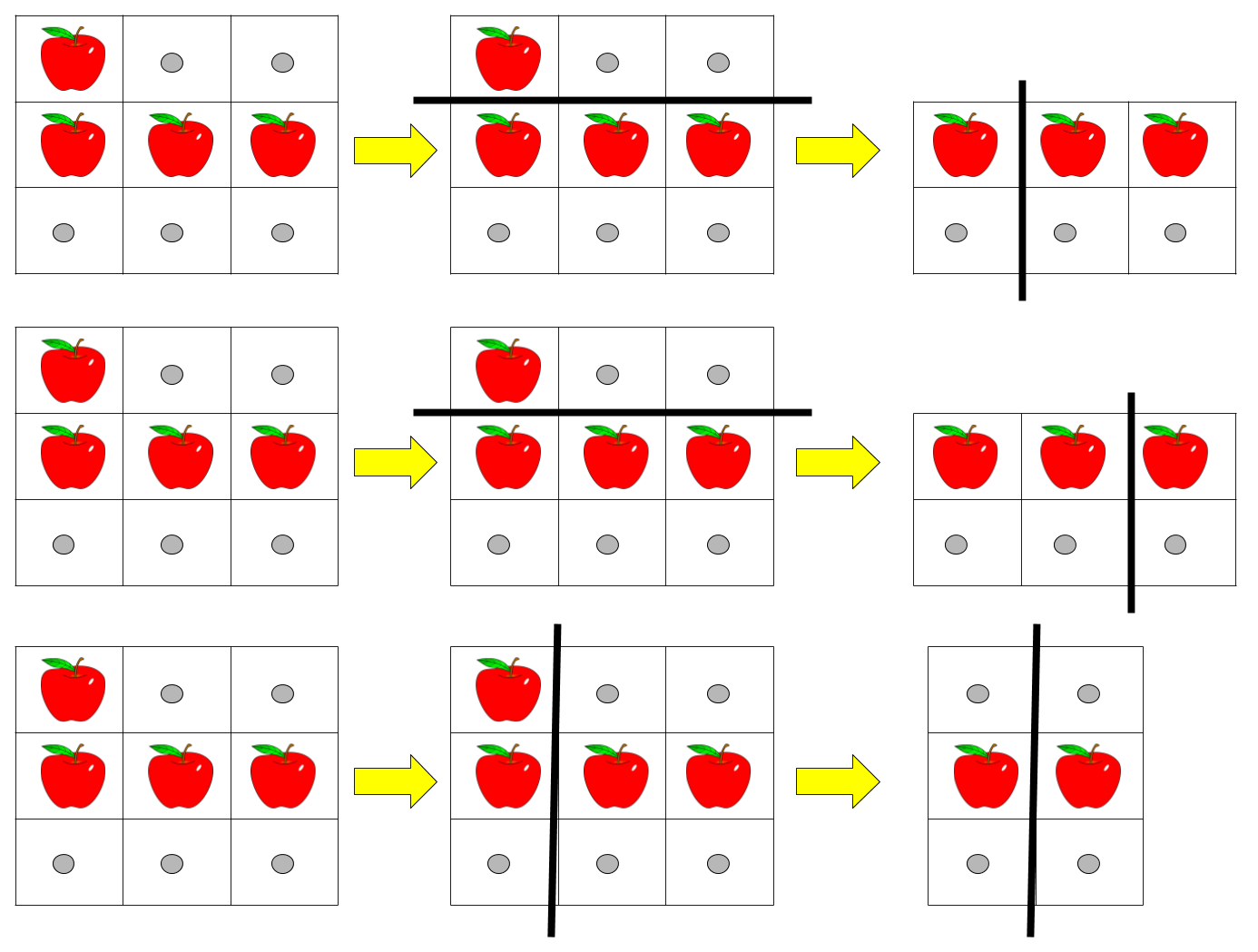
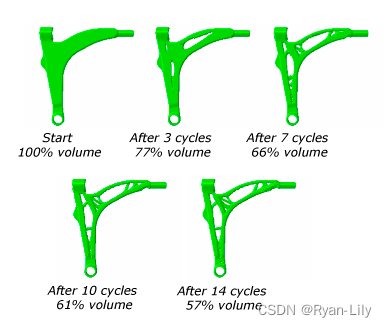
输入：pizza = ["A..","AAA","..."], k = 3
输出：3 
解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。

示例 2：

输入：pizza = ["A..","AA.","..."], k = 3
输出：1

示例 3：

输入：pizza = ["A..","A..","..."], k = 1
输出：1

提示：

1 <= rows, cols <= 50
rows == pizza.length
cols == pizza[i].length
1 <= k <= 10
pizza 只包含字符 'A' 和 '.' 。

解题思路

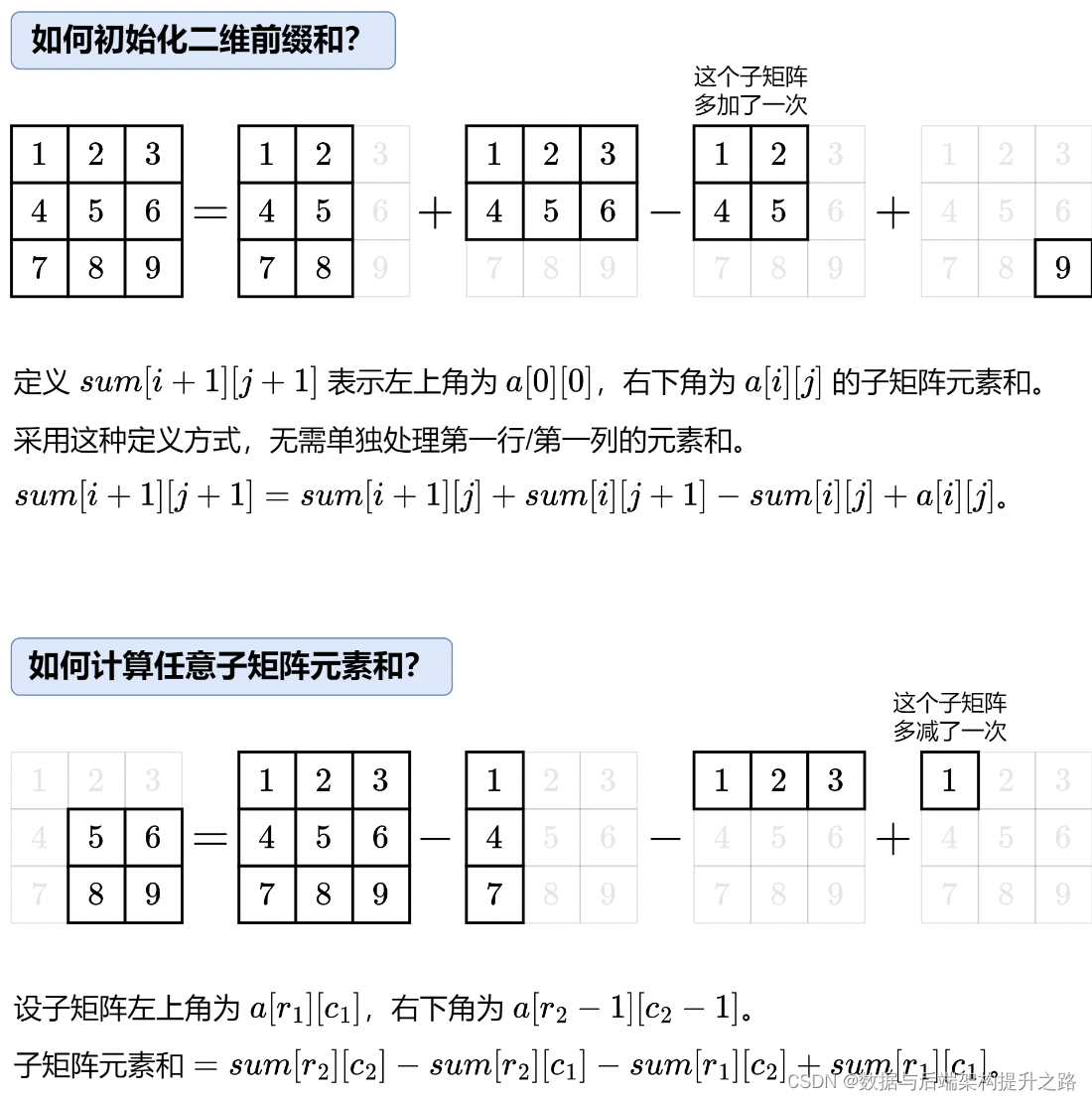
模版代码

class MatrixSum:
    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), len(matrix[0])
        preSum = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(matrix):
            for j, x in enumerate(row):
                preSum[i + 1][j + 1] = preSum[i + 1][j] + preSum[i][j + 1] - preSum[i][j] + x
        self.preSum = preSum

    # 返回左上角在 (r1,c1) 右下角在 (r2-1,c2-1) 的子矩阵元素和（类似前缀和的左闭右开）
    def query(self, r1: int, c1: int, r2: int, c2: int) -> int:
        return self.preSum[r2][c2] - self.preSum[r2][c1] - self.preSum[r1][c2] + self.preSum[r1][c1]

    # 如果你不习惯左闭右开，也可以这样写
    # 返回左上角在 (r1,c1) 右下角在 (r2,c2) 的子矩阵元素和
    def query2(self, r1: int, c1: int, r2: int, c2: int) -> int:
        return self.preSum[r2 + 1][c2 + 1] - self.preSum[r2 + 1][c1] - self.preSum[r1][c2 + 1] + self.preSum[r1][c1]

最终题解

class Solution:
 
    MOD = 10**9 + 7
    def ways(self, pizza: List[str], k: int) -> int:

        rows, cols = len(pizza), len(pizza[0])

        # preSum[row][col] 表示从 (row, col) 到披萨矩形右下角部分的苹果（'A'字符）总数量。
        preSum = [[0 for _ in range(cols + 1)] for _ in range(rows + 1)]
        for row in range(rows - 1, -1, -1):
            for col in range(cols - 1, -1, -1):
                preSum[row][col] = preSum[row + 1][col] + preSum[row][col + 1] - preSum[row + 1][col + 1] + (pizza[row][col] == 'A')
        
        # dp[i][j][l]表示以(i, j)为左上角，到披萨右下角为止的子矩阵，
        # 能够通过l次切割（实际上获得l+1块披萨）的方案数。所有的切割都会发生在这个子矩阵的区域内。
        dp = [[[0 for _ in range(k)] for _ in range(cols)] for _ in range(rows)]
        
        # 预先填充至少有一个苹果的单块情况
        for row in range(rows):
            for col in range(cols):
                # 只有当至少有一个苹果时，方案才为1
                dp[row][col][0] = preSum[row][col] > 0
        
        for l in range(1, k): # 从1开始，0已经处理过
            for row in range(rows):
                for col in range(cols):
                    #尝试所有水平切割的可能
                    for x in range(row + 1, rows):  
                        if preSum[row][col] - preSum[x][col] > 0: # 确定上半部分至少一个苹果
                            dp[row][col][l] += dp[x][col][l-1]
                            dp[row][col][l] %=  self.MOD
                    #尝试所有垂直切割的可能
                    for y in range(col + 1, cols):
                        if preSum[row][col] - preSum[row][y] > 0: # 确定左半部分至少一个苹果
                        # 假设我们在位置 (row, y) 处进行一个垂直切割（
                        # 切割线位于第 y 列的右侧，因此切下的左侧区域是从第 row 行到第 y 列的子矩阵）。
                        # 该垂直切割将披萨分割为左侧的一块（包含至少一个苹果）和右侧的一块。
                        # 这个刚切割的左块符合我们要求的l+1块的其中一块。
                            dp[row][col][l] += dp[row][y][l-1]
                            dp[row][col][l] %= self.MOD
        
        return int(dp[0][0][k - 1])