⭐前言⭐

※※※大家好！我是同学〖森〗，一名计算机爱好者，今天让我们进入刷题模式。若有错误，请多多指教。更多有趣的代码请移步Gitee

👍 点赞 ⭐ 收藏 📝留言都是我创作的最大的动力！

合抱之木，生于毫末；九层之台，起于垒土；千里之行，始于足下。

⭐目录⭐

1）题目

2）思路分析及其代码

一、暴力求解

二、哈希表

合抱之木，生于毫末；九层之台，起于垒土；千里之行，始于足下。

1）题目

两数之和 LeetCode HOT 100

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

输入：nums = [3,2,4], target = 6

输出：[1,2]

输入：nums = [3,3], target = 6

输出：[0,1]

2）思路分析及其代码

一、暴力求解

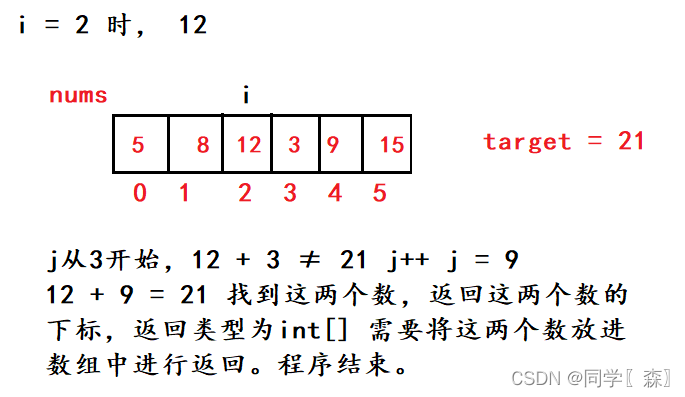
nums和target如图所示

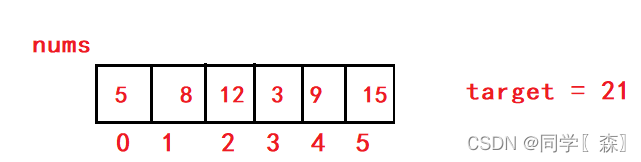
题目分析

循环过程

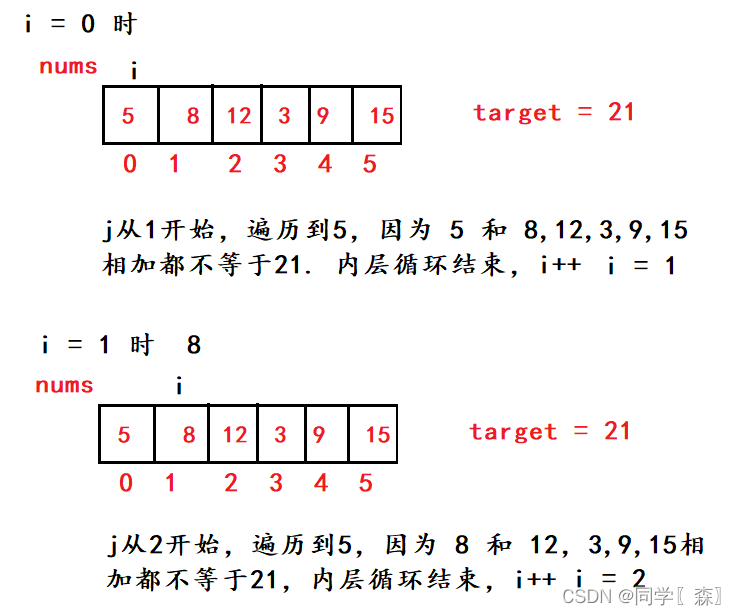
原码

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int len = nums.length;
        for(int i = 0; i < len; i++) {
            //外层循环，确定第一个加数
            for(int j = i + 1; j < len; j++){
                //内层循环，确定第二个加数
                if(target == nums[i] + nums[j]) {
                    //判断条件
                    return new int[] {i, j};  // 返回的下标放进数组中
                }
            }
        }
        return new int[] {0};
    }
}

时间复杂度：O（N^2）外层循环 + 内层循环。最坏情况是最后两个数是要找的数。每两个数都有匹配一遍。

空间复杂度：O（1）没有用到额外的空间

二、哈希表

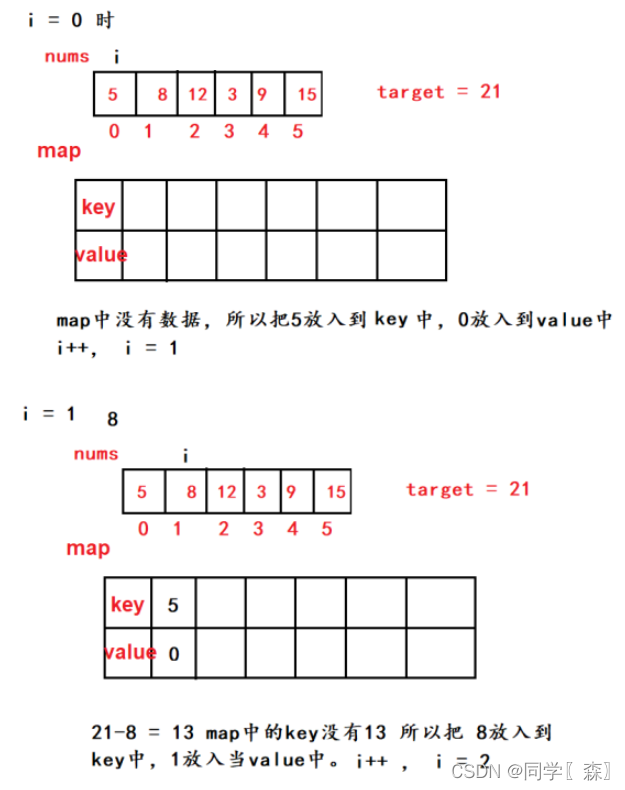
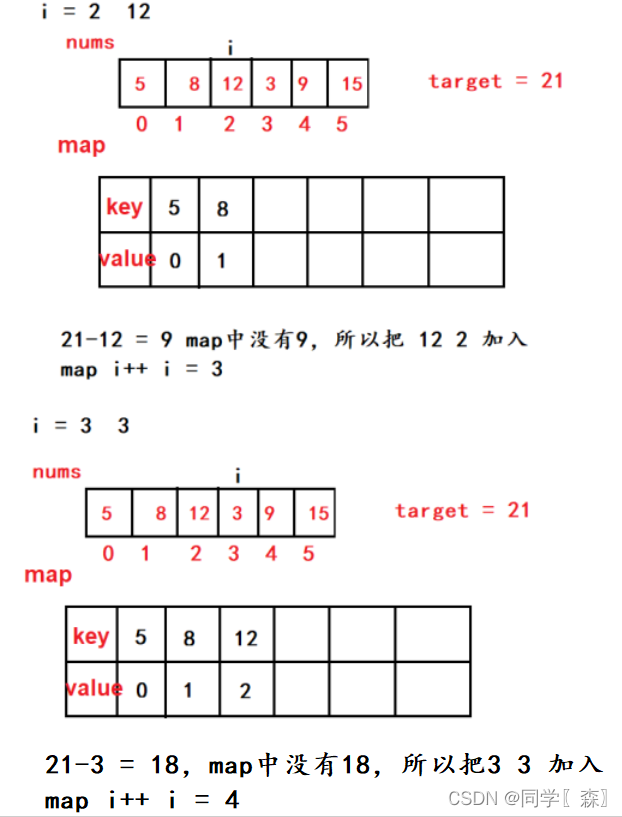
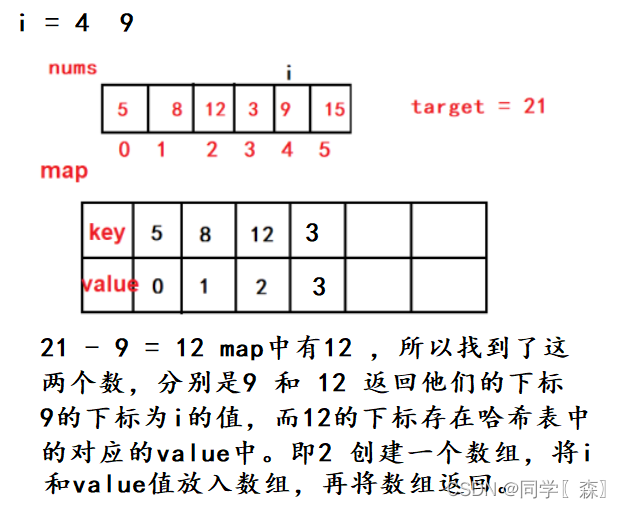
题目分析

过程分析

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        //创建哈希表
        for(int i = 0; i < nums.length; i++) {
            if(map.containsKey(target - nums[i]) ) {
                //判断是否在哈希表中存在第二个数，由原来的循环变成了判断。
                //时间复杂度降低,空间复杂度提高。用空间换取时间。
                return new int[] {map.get(target - nums[i]), i}; 
                //注意返回顺序，i在后面，后返回
            }
            map.put(nums[i], i); //将数组的值和下标存放进哈希表。
        }
        return new int[] {0};
    }
}