[NOIP2017 提高组] 奶酪（C++，并查集）

news2024/11/26 0:53:22

题目背景

NOIP2017 提高组 D2T1

题目描述

现有一块大奶酪，它的高度为 $h$ ，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为 $z = 0$ ，奶酪的上表面为 $z = h$ 。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑到奶酪的上表面去?

空间内两点 $P_1(x_1,y_1,z_1)$ 、 $P2(x_2,y_2,z_2)$ 的距离公式如下：

$\mathrm{dist}(P_1,P_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

输入格式

每个输入文件包含多组数据。

第一行，包含一个正整数 $T$ ，代表该输入文件中所含的数据组数。

接下来是 $T$ 组数据，每组数据的格式如下：第一行包含三个正整数 $n, h, r$ ，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。

接下来的 $n$ 行，每行包含三个整数 $x, y, z$ ，两个数之间以一个空格分开，表示空洞球心坐标为 $(x, y, z)$ 。

输出格式

$T$ 行，分别对应 $T$ 组数据的答案，如果在第 $i$ 组数据中，Jerry 能从下表面跑到上表面，则输出 Yes，如果不能，则输出 No。

样例 #1

样例输入 #1

样例输出 #1

Yes
No
Yes

提示

【输入输出样例 $1$ 说明】

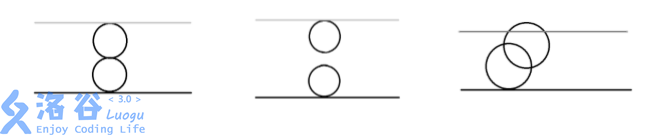
第一组数据,由奶酪的剖面图可见：

第一个空洞在 $(0, 0, 0)$ 与下表面相切；

第二个空洞在 $(0, 0, 4)$ 与上表面相切；

两个空洞在 $(0, 0, 2)$ 相切。

输出 Yes。

第二组数据,由奶酪的剖面图可见：

两个空洞既不相交也不相切。

输出 No。

第三组数据,由奶酪的剖面图可见：

两个空洞相交，且与上下表面相切或相交。

输出 Yes。

【数据规模与约定】

对于 $20\%$ 的数据， $n = 1$ ， $\le h$ ， $\le 10^4$ ，坐标的绝对值不超过 $10^4$ 。

对于 $40\%$ 的数据， $\le n \le 8$ ， $\le h$ ， $\le 10^4$ ，坐标的绝对值不超过 $10^4$ 。

对于 $80\%$ 的数据， $\le n \le 10^3$ ， $\le h , r \le 10^4$ ，坐标的绝对值不超过 $10^4$ 。

对于 $100\%$ 的数据， $\le n \le 1\times 10^3$ ， $\le h , r \le 10^9$ ， $\le 20$ ，坐标的绝对值不超过 $10^9$ 。

解题思路：

这里就不介绍并查集了，放一篇我写的并查集传送门qwq，传送门

为什么本题用并查集解决呢？

我们可以对题意进行抽象，把所有与底层连通的空洞作为起点集合，把所有与顶层连通的空洞作为终点集合

那么我们遍历尝试将所有可能的两个点合并为一个集合

最后检查起点集合和终点集合会不会合并即可

引用一句从别的地方学来的话：“凡是涉及到元素的分组管理，都可以考虑用并查集来维护。”

AC代码如下

//并查集
#include <iostream>
#include <cmath>
using namespace std;
const int max_n = 1e3;

int fa[max_n + 3] = { 0 };//根节点
int dep[max_n + 3] = { 0 };//深度
struct node { int x, y, z; }nodes[max_n + 3];//存图

//初始化
void init(int n) {
	for (int i = 1; i <= n; i++) {
		fa[i] = i;
		dep[i] = 1;
	}
}

//寻访根节点
int find(int x) {
	return fa[x] == x ? x : (fa[x] = find(fa[x]));
}

//按秩合并
void merge(int x, int y) {
	int t1 = find(x);
	int t2 = find(y);
	if (dep[t1] >= dep[t2]) fa[t2] = fa[t1];
	else fa[t1] = fa[t2];

	if (dep[t1] == dep[t2]) dep[t1]++;
}

//是否相通
bool is_connect(int x, int y, const long long& r) {
	long long distance = (long long)(nodes[x].x - nodes[y].x) * (long long)(nodes[x].x - nodes[y].x) +
		(long long)(nodes[x].y - nodes[y].y) * (long long)(nodes[x].y - nodes[y].y) +
		(long long)(nodes[x].z - nodes[y].z) * (long long)(nodes[x].z - nodes[y].z);
	if (4l * r * r >= distance) return true;
	else return false;
}

//是否同集合
bool is_same_tree(int x, int y) {
	if (find(x) == find(y)) return true;
	else return false;
}

int main() {
	int T, n, h, r, x, y, z;
	bool special;
	cin >> T;
	for (int i = 0; i < T; i++) {
		cin >> n >> h >> r;
		//初始化
		special = false;
		fa[0] = 0; dep[0] = 1;
		nodes[0] = { 0,0,0 };//底层
		fa[n + 1] = n + 1; dep[n + 1] = 1;
		nodes[n + 1] = { 0,0,h };//顶层
		init(n);
		for (int j = 1; j <= n; j++) {//存图
			cin >> x >> y >> z;
			nodes[j] = { x,y,z };
			if (z + r >= h) fa[j] = fa[n + 1];
			if (z - r <= 0) fa[j] = fa[0];
			if (z + r >= h && z - r <= 0) {//特判
				special = true;
			}
		}
		if (special) {
			cout << "Yes" << endl;
			continue;
		}

		//合并
		for (int j = 1; j <= n - 1; j++) {
			for (int z = j + 1; z <= n; z++) {
				if (!is_same_tree(j, z) && is_connect(j, z, r)) merge(j, z);
			}
		}

		if (find(0) == find(n + 1)) cout << "Yes" << endl;
		else cout << "No" << endl;
	}
	return 0;
}