有华为OD考试扣扣交流群可加948025485
可上全网独家的 欧弟OJ系统 练习华子OD、大厂真题
绿色聊天软件戳 od1336了解算法冲刺训练

题目链接

LeetCode2641、二叉树的堂兄弟节点II

题目描述

给你一棵二叉树的根 root ，请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。

如果两个节点在树中有相同的深度且它们的父节点不同，那么它们互为 堂兄弟 。

请你返回修改值之后，树的根 root 。

注意，一个节点的深度指的是从树根节点到这个节点经过的边数。

示例 1：

• 输入：

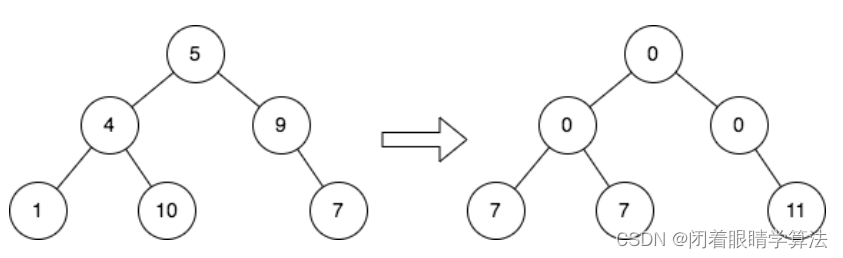
root = [5,4,9,1,10,null,7]
输出：[0,0,0,7,7,null,11]
解释：上图展示了初始的二叉树和修改每个节点的值之后的二叉树。 值为 5 的节点没有堂兄弟，所以值修改为 0 。 值为 4 的节点没有堂兄弟，所以值修改为 0 。 值为 9 的节点没有堂兄弟，所以值修改为 0 。 值为 1 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。 值为 10 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。 值为 7 的节点有两个堂兄弟，值分别为 1 和 10 ，所以值修改为 11 。

示例 2：

• 输入：root = [3,1,2]
• 输出：[0,0,0]
• 解释：上图展示了初始的二叉树和修改每个节点的值之后的二叉树。 值为 3 的节点没有堂兄弟，所以值修改为 0 。 值为 1 的节点没有堂兄弟，所以值修改为 0 。 值为 2 的节点没有堂兄弟，所以值修改为 0 。

提示：

• 树中节点数目的范围是 [1, 10(5)] 。
• 1 <= Node.val <= 10(4)

解题思路

需要考虑到相同层的其他节点的值，很容易想到使用BFS来完成。

本题难点在于，如何高效地将某个节点的所有堂兄弟节点之和cousin_sum算出来。

假设某一层的所有节点和cur_level_sum已知，某个节点node的和其同一个父节点的兄弟的节点和bro_sum已知，那么存在cousin_sum = cur_level_sum - bro_sum成立。可以将node的值修改为cousin_sum

那么问题进一步退化，在BFS过程中，某一个节点node出队时，如何已知cur_level_sum和bro_sum？

由于在BFS的过程中，每一个节点都会考虑其子节点，显然其子节点的值的和child_sum也是可以迅速算到的。即

child_sum = 0
child_sum += node.left.val  if node.left  else 0
child_sum += node.right.val if node.right else 0    

当node的子节点node.left或node.right入队时，我们可以将node的child_sum和子节点一起存入队列中，那么当子节点node.left或node.right出队时，node的child_sum就是子节点node.left或node.right的bro_sum了。

cur_level_sum的计算也是类似的。在某一层节点出队的时候，下一层的总和nxt_level_sum由当前层的所有节点的所有子节点的值求和获得，即可以将所有node的child_sum叠加得到。那么在遍历到下一层的时候，下一层的cur_level_sum就是上一层的nxt_level_sum了。

上述过程就可以用一次遍历完成node的值的修改了。

代码

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        q = deque()
        q.append([root, root.val])
        nxt_level_sum = root.val
        while q:
            cur_level_sum = nxt_level_sum
            nxt_level_sum = 0
            q_size = len(q)
            for _ in range(q_size):
                # 弹出节点node以及node的兄弟节点和bro_sum
                node, bro_sum = q.popleft()
                # 当前层的和减去node的兄弟和bro_sum，为node的堂兄弟节点和cousin_sum
                cousin_sum = cur_level_sum - bro_sum
                # 将node的值修改为cousin_sum
                node.val = cousin_sum
                # 初始化node的孩子节点的和为child_sum
                child_sum = 0
                # 如果左孩子/右孩子存在，则更新child_sum
                child_sum += node.left.val  if node.left  else 0
                child_sum += node.right.val if node.right else 0     
                # 如果左孩子/右孩子存在，则将子节点和child_sum存入队列中
                # 对于孩子节点node.left或node.right而言，child_sum是他们的兄弟节点和
                if node.left:
                    q.append([node.left, child_sum])
                if node.right:
                    q.append([node.right, child_sum])
                # 更新下一层的节点和nxt_level_sum
                nxt_level_sum += child_sum      
        return root           
            

Java

class Solution {
    public TreeNode replaceValueInTree(TreeNode root) {
        if (root == null) return null;

        Queue<Pair<Integer, TreeNode>> q = new ArrayDeque<>();
        q.offer(new Pair<>(root.val, root));

        int nextLevelSum = root.val;
        int currentLevelSum = 0;
        while (!q.isEmpty()) {
            currentLevelSum = nextLevelSum;
            nextLevelSum = 0;
            int size = q.size();

            for (int i = 0; i < size; ++i) {
                Pair<Integer, TreeNode> pair = q.poll();
                int siblingSum = pair.getKey();
                TreeNode node = pair.getValue();
                int childSum = 0;
                node.val = currentLevelSum - siblingSum;
                if (node.left != null) 
                    childSum += node.left.val;
                if (node.right != null) 
                    childSum += node.right.val;
                if (node.left != null) 
                    q.offer(new Pair<>(childSum, node.left));
                if (node.right != null) 
                    q.offer(new Pair<>(childSum, node.right));

                nextLevelSum += childSum;
            }
        }

        return root;
    }
}

C++

class Solution {
public:
    TreeNode* replaceValueInTree(TreeNode* root) {
        if (root == nullptr) return nullptr;

        queue<pair<int, TreeNode*>> q;
        q.push({root->val, root});

        int nextLevelSum = root->val;
        int currentLevelSum = 0;
        while (!q.empty()) {
            currentLevelSum = nextLevelSum;
            nextLevelSum = 0;
            int size = q.size();

            for (int i = 0; i < size; ++i) {
                auto [siblingSum, node] = q.front();
                q.pop();
                int childSum = 0;
                node->val = currentLevelSum - siblingSum;
                if (node->left != nullptr) 
                    childSum += node->left->val;
                if (node->right != nullptr) 
                    childSum += node->right->val;
                if (node->left != nullptr) 
                    q.push({childSum, node->left});
                if (node->right != nullptr) 
                    q.push({childSum, node->right});

                nextLevelSum += childSum;
            }
        }

        return root;
    }
};

时空复杂度

时间复杂度：O(N)。

空间复杂度：O(N)。

---

华为OD算法/大厂面试高频题算法练习冲刺训练

• 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务100+同学成功上岸！

• 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

• 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

• 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

• 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

• 可查看链接 大厂真题汇总 & OD真题汇总(持续更新)

• 绿色聊天软件戳 od1336了解更多