代码随想录算法训练营DAY14

代码随想录算法训练营DAY14 | 二叉树 (1)

news2024/11/15 8:35:50

一、二叉树理论基础

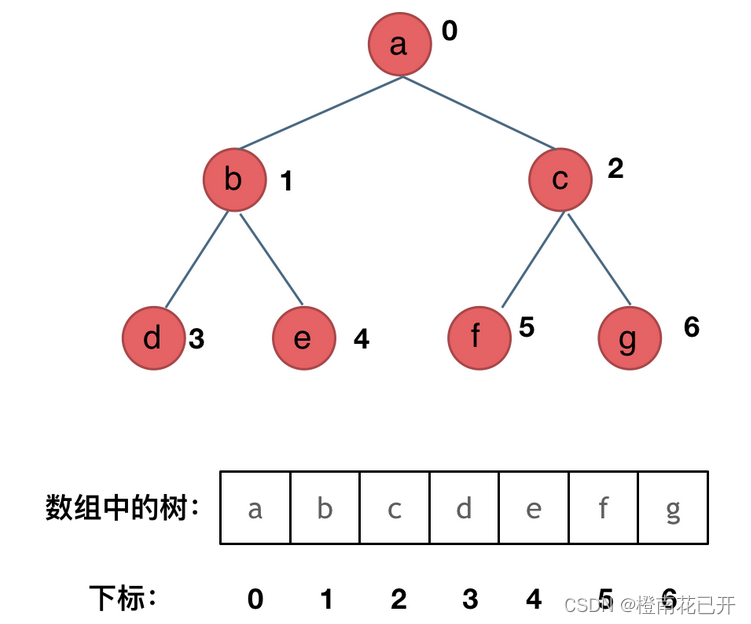
1.存储方式

链式存储：

顺序存储：

2.二叉树标准定义(Java)

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { 
        this.val = val; 
    }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

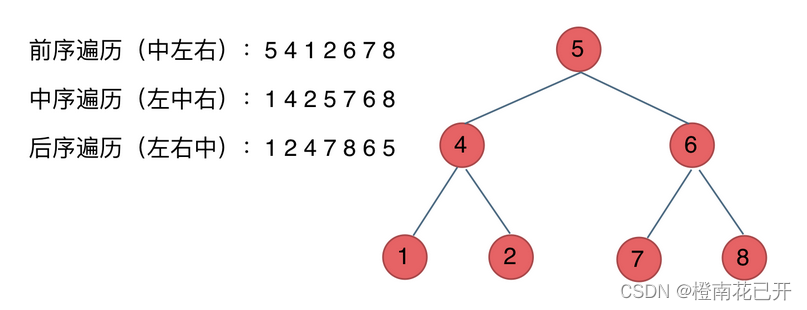
3.遍历方式

深度优先遍历 (DFS)：先往深处走，遇到叶子结点再往回走；二叉树中又分为前序遍历、中序遍历、后序遍历(以中间节点的位置划分)。

4.常见二叉树种类

满二叉树：只有度为0的结点和度为2的结点，并且度为0的结点在同一层上。

完全二叉树：

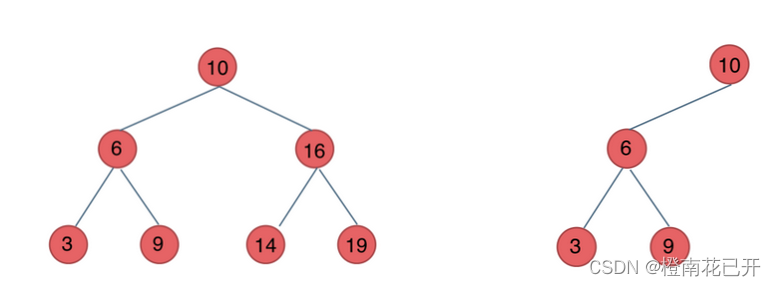
搜索二叉树：

平衡搜索二叉树：是一棵空树或它的左右两个子树的高度差的绝对值不超过1，且左右子树都为平衡二叉树。

二、二叉树的递归遍历

1.递归三要素

确定递归函数的参数和返回值、确定终止条件、确定单层递归的逻辑。

2. 遍历代码

//前序遍历
public void pre(TreeNode node, List<Integer> list){
        if(node == null){
            return;
        }
        list.add(node.val);
        pre(node.left,list);
        pre(node.right,list);
        return;
}
//中序遍历
public void mid(TreeNode node, List<Integer> list){
        if(node == null){
            return;
        }
        mid(node.left,list);
        list.add(node.val);
        mid(node.right,list);
        return;
}
//后序遍历
public void post(TreeNode node, List<Integer> list){
        if(node == null){
            return;
        }
        post(node.left,list);
        post(node.right,list);
        list.add(node.val);
        return;
}

3.相关题目

144.二叉树的前序遍历

94.二叉树的中序遍历

145.二叉树的后序遍历

三、二叉树的迭代遍历

1.前序遍历

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> ans = new LinkedList<>();
        if(root == null){
            return ans;
        }
        stack.push(root);
        //中左右
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            ans.add(node.val);
            if(node.right != null){
                stack.push(node.right);
            }
            if(node.left != null){
                stack.push(node.left);
            }
        }
        return ans;
    }
}

2.后序遍历

后序遍历与前序遍历逻辑类似~

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> ans = new LinkedList<>();
        if(root == null){
            return ans;
        }
        stack.push(root);
        //中右左
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            ans.add(node.val);
            if(node.left != null){
                stack.push(node.left);
            }
            if(node.right != null){
                stack.push(node.right);
            }
        }
        //颠倒顺序->左右中
        List<Integer> result = new LinkedList<>();
        while(!ans.isEmpty()){
            result.add(ans.removeLast());
        }
        return result;
    }
}

3.中序遍历

中序遍历为“左中右”，因而需要一个指针来协助访问ovo

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ans = new LinkedList<>();
        if(root == null){
            return ans;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while(cur != null || !stack.isEmpty()){
            if(cur != null){
                //左
                stack.push(cur);
                //一直向左走到底
                cur = cur.left;
            }else{
                //要处理的数据
                cur = stack.pop();
                //中
                ans.add(cur.val);
                //右
                cur = cur.right;
            }
        }
        return ans;
    }
}