算法每日一题：使用循环数组所有元素相等的最少秒数

算法每日一题：使用循环数组所有元素相等的最少秒数 | 哈希

news2024/10/6 10:35:45

大家好，我是星恒，今天给大家带来的是一道需要感觉规律的题目，只要读懂题目中的规律，就可以做出来了
这道题用到了哈希，还有一个关键点比较类似循环队列

题目：leetcode 2808

给你一个下标从 0 开始长度为 n 的数组 nums 。
每一秒，你可以对数组执行以下操作：

对于范围在 [0, n - 1] 内的每一个下标 i ，将 nums[i] 替换成 nums[i] ，nums[(i - 1 + n) % n] 或者 nums[(i + 1) % n] 三者之一。

注意，所有元素会被同时替换。
请你返回将数组 nums 中所有元素变成相等元素所需要的最少秒数。

示例 1：

输入：nums = [1,2,1,2]
输出：1
解释：我们可以在 1 秒内将数组变成相等元素：
- 第 1 秒，将每个位置的元素分别变为 [nums[3],nums[1],nums[3],nums[3]] 。变化后，nums = [2,2,2,2] 。
1 秒是将数组变成相等元素所需要的最少秒数。

示例 2：

输入：nums = [2,1,3,3,2]
输出：2
解释：我们可以在 2 秒内将数组变成相等元素：
- 第 1 秒，将每个位置的元素分别变为 [nums[0],nums[2],nums[2],nums[2],nums[3]] 。变化后，nums = [2,3,3,3,3] 。
- 第 2 秒，将每个位置的元素分别变为 [nums[1],nums[1],nums[2],nums[3],nums[4]] 。变化后，nums = [3,3,3,3,3] 。
2 秒是将数组变成相等元素所需要的最少秒数。

示例 3：

输入：nums = [5,5,5,5]
输出：0
解释：不需要执行任何操作，因为一开始数组中的元素已经全部相等。

提示：

1 <= n == nums.length <= 105
1 <= nums[i] <= 109

分析：
阅读题目，大家首先可能对这两个式子有些迷惑：nums[(i - 1 + n) % n] 和 nums[(i + 1) % n]
其实他们就是处理了一下首尾元素：

nums[(i - 1 + n) % n]：当元素为首元素时（下标为0），式子变为了nums[n - 1]；其他元素相当于nums[i - 1]
nums[(i + 1) % n]：当元素为尾元素时（下标为n - 1），式子变为了nums[0]；其他元素相当于nums[i + 1]

这样做的目的是可以让首尾相连，感觉首元素和尾元素相邻了

好，知道了这个，我们正式开始分析这道题目：
读题，我们可以知道，一个元素，一次可以将相邻的两个元素下标变为自己的，所以每一秒我们可以影响相邻元素。

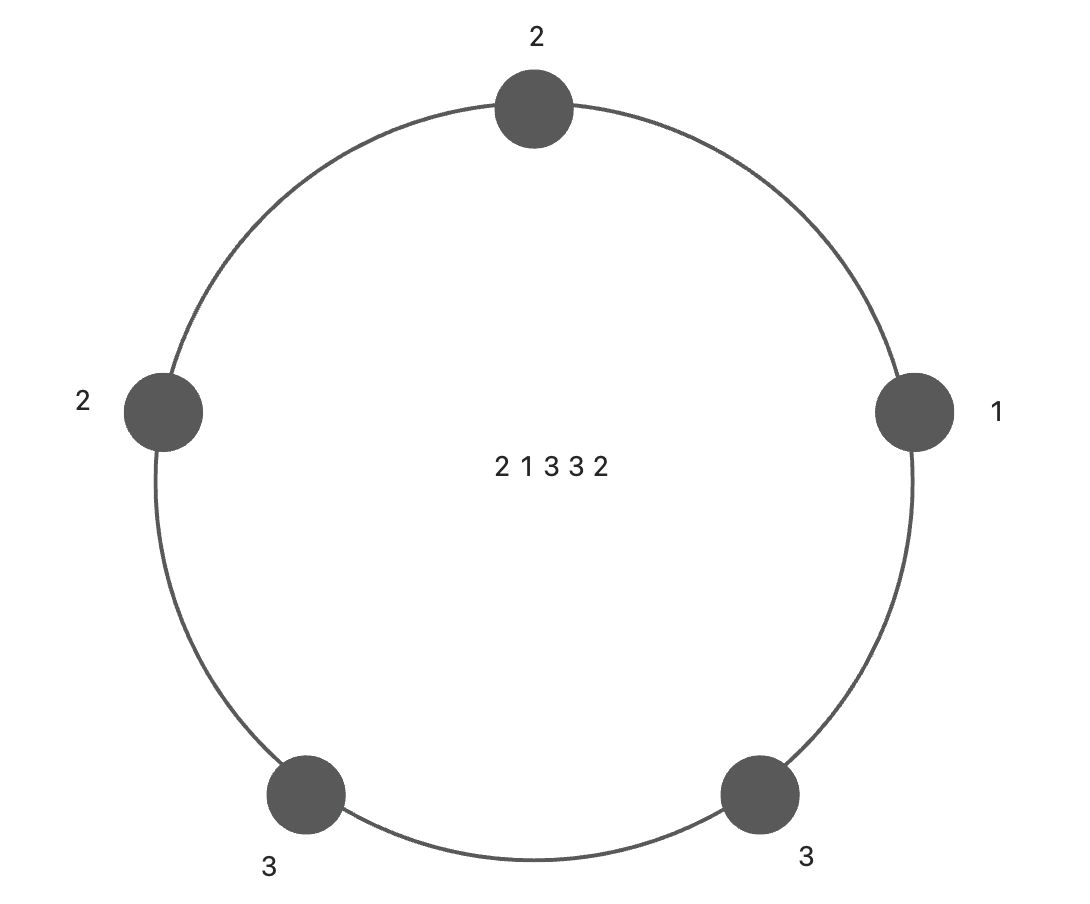
结合上面的理论，我们来看这个图

也就是说，变成相等元素所需要的最少秒数，就是两个相邻相同元素的最大距离 / 2
注意，首尾距离也要计算

至于我们选择哪个作为相同元素更好，我们只要将每一种元素的所需最大秒数求出来比较就可以了

我们来看题解：

题解：

class Solution {
    public int minimumSeconds(List<Integer> nums) {
        HashMap<Integer, List<Integer>> mp = new HashMap<>();
        int n = nums.size(), res = n;
        for (int i = 0; i < n; ++i) {
            mp.computeIfAbsent(nums.get(i), k -> new ArrayList<>()).add(i);
        }
        for (List<Integer> positions : mp.values()) {
            int mx = positions.get(0) + n - positions.get(positions.size() - 1);
            for (int i = 1; i < positions.size(); ++i) {
                mx = Math.max(mx, positions.get(i) - positions.get(i - 1));
            }
            res = Math.min(res, mx / 2);
        }
        return res;
    }
}