算法day10

• 20 有效的括号
• 1047 删除字符串中的所有相邻重复性
• 150 逆波兰表达式求值

---

20 有效的括号

拿到这个题的想法，首先我在想我能不能用数组的操作来扫描做。后来想想，如果这样做那特判也太多了，不好做。然后第二个想法就是用栈来做，我之前看过有类似的算法题，但是具体细节怎样我忘了。这里我就之间看题解学习了。

看完解题我回来了：

括号匹配时使用栈解决的经典问题，题意要求：就是和我们平时写代码的顺序一样，有左括号，相应的位置必须要有右括号。

由于栈结构的特殊性，非常适合左对称匹配类型的题目
做这个题之前，首先要弄清楚，字符串括号不匹配有几种情况。
看几个不匹配的例子：
1.这个显然左边第一个多了

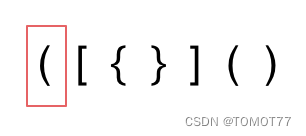
2.这个显然里面这两个对不上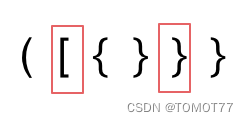
3.这个就是多余了。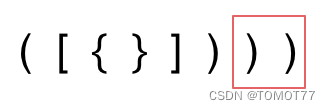

现在来看这个题的思路是怎样的
我个人看这个图的适合感觉这个是最好理解的：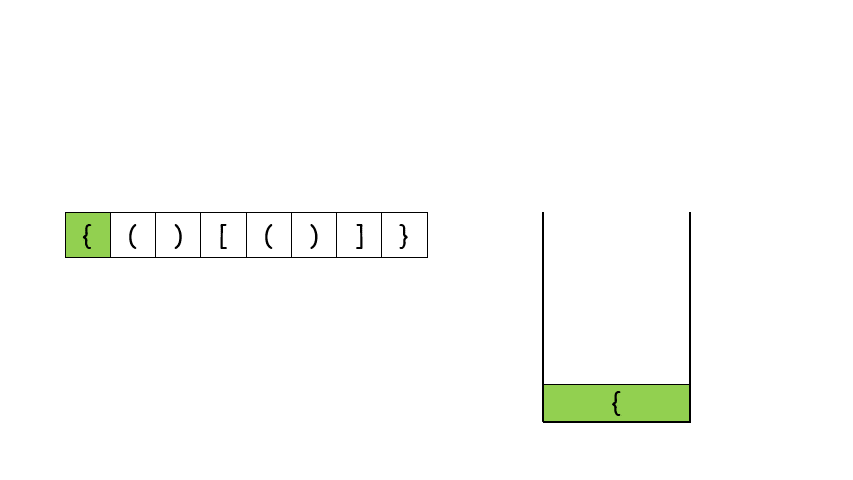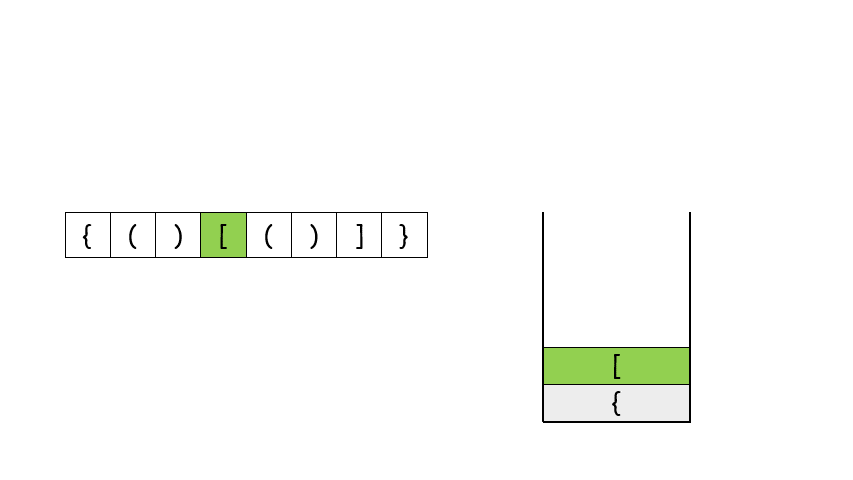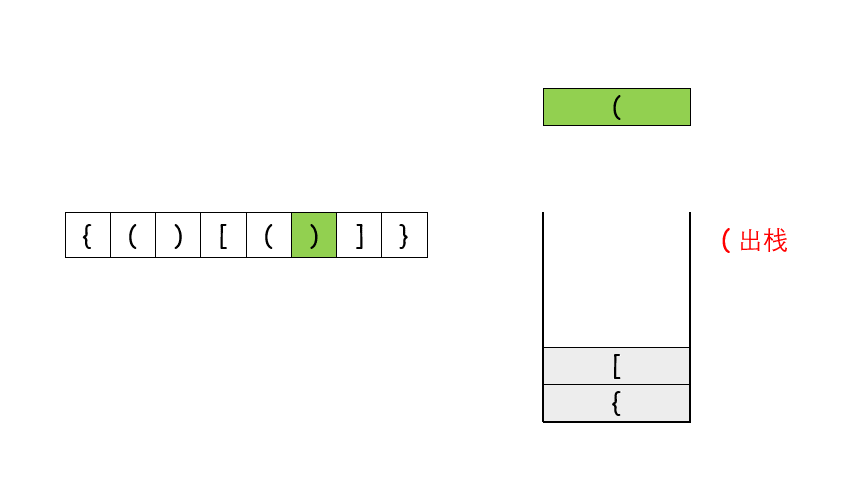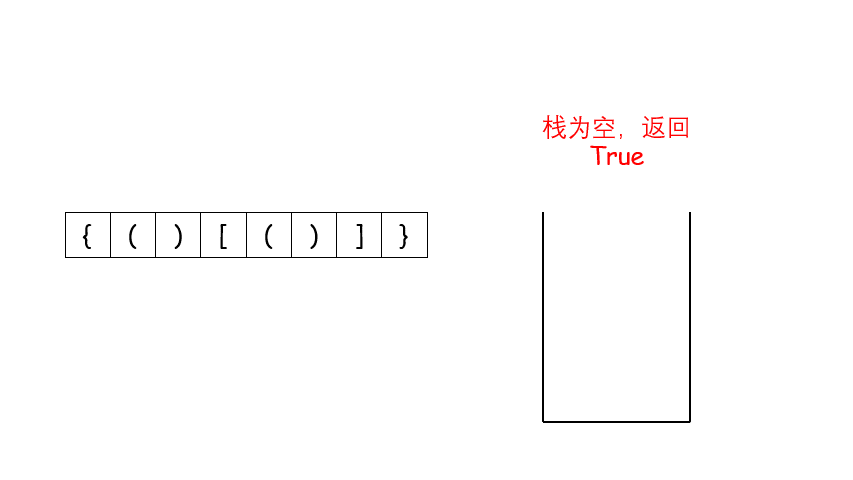
这个图体现了怎样的算法思路：
首先我先创建一个空栈。
是左括号，那就之间入栈，如果是右括号那就要进行弹栈，但是这个弹栈操作要注意。

接下来细说弹栈操作：从这个图我们可以发现一件事，你遇见的第一个右括号比如这个括号我记为}，然后可以发现这个栈顶元素，它必须是这个}相应的{，如果不是或者栈中已经没有左括号了，那就说明字符串s直接无效，并返回False，为了快速判断括号的类型，我们可以使用哈希表存储每一种括号。哈希表的键为右括号，值为相同类型的左括号。

在遍历结束后，如果栈中啥也没有，则可以返回true了，否则返回False。

还可以有一个小优化
如果字符串的长度为奇数可以直接返回false，节省计算的次数。

下面来看代码怎么写的

正确代码：

func isValid(s string) bool {
    hash := map[byte]byte{')':'(', ']':'[', '}':'{'}
    stack := make([]byte, 0)
    if s == "" {
        return true
    }

    for i := 0; i < len(s); i++ {
        if s[i] == '(' || s[i] == '[' || s[i] == '{' {
            stack = append(stack, s[i])
        } else if len(stack) > 0 && stack[len(stack)-1] == hash[s[i]] {
            stack = stack[:len(stack)-1]
        } else {
            return false
        }
    }
    return len(stack) == 0
}

这个代码逻辑可以说和我上面解释的一模一样。别去看官方题解那个代码，写的太花里胡哨了。

总结：
1.需要一个map，来存右括号的映射（如果你不用映射，你就要写一堆的if判断，所以这里放心用map，而且空间复杂度的大头根本就不是这个map，这个map可以说是常数级的空间，空间复杂度主要取决于这个栈，这个栈的空间复杂度达到了o(n)）.
2.需要一个栈进行消除。

思考：
(1).我今天看到这个题解又有了一点go语言语法积累：
以前我一直认为在go语言中，string类型的字符串 ，对下标的操作是不行的。然后我在这个题解中发现是可以的。
这里进行改正：
在go语言中，确实可以通过下标访问字符串的单个字符。但它获取的实质并不是字符，这样做实际上是访问字符串中相应位置的字节，而不是字符。因为Go中字符串是按字节组织的，并且默认使用UTF-8编码。
当我使用下标访问字符串，比如s[i]，我得到的是字符串在i位置上的字节，如果字符串包含多字节的UTF-8字符，单个字节可能不代表完整字符。
这里举个例子：
1.s:=“hello”

fmt.Println(s[0]) // 输出 104, 即 'h' 的 ASCII 码
fmt.Println(s[1]) // 输出 101, 即 'e' 的 ASCII 码

如果我真想把h输出，那就要格式化输出：

s := "hello"
fmt.Printf("%c\n", s[0]) // 将输出字符 'h'

s := "你好"
fmt.Println(s[0]) // 不会输出 '你' 或 '好'，而是输出一个字节的值

因为汉字是三字节，这里会输出 你 这个汉字的第一个字节，这个汉字的字节多半都是大于127的。

(2)我的map的初始化写的也不是很好，这部分的语法就在这里补起来
hash := map[byte]byte{‘)’:‘(’, ‘]’:‘[’, ‘}’:‘{’}
这个初始化我当时忘了，我真是服了。
就直接写好map了后面{}，直接写键值对，然后用逗号进行分割就行。

（3）我写的时候还犯了一个有关数据错误，因为我在操作有关字符的时候都喜欢用rune这个数据类型，但是我在访问s[i]的时候出现了数据不匹配的情况，这里主要是我对rune和byte没有清楚的认识：
在go语言中rune是int32的别名，byte是uint8的别名。这里在访问字符s[i]的时候要小心，因为字符串是字节组织的。

---

1047删除字符串中的所有相邻重复性

这题我上来想的还是暴力：
字符串先转切片，设置一个bool遍历judge判断是否删干净，然后遍历切片检查是否有重复相邻，有就用切片操作删除这两个切片元素。删干净了judge=true，然后返回结果。

这个解法是可以过的，但是时间复杂度太高了，是o(n^2)
暴力解

func removeDuplicates(s string) string {
    runes := []rune(s)
    for {
        judge := false
        for i := 1; i < len(runes); i++ {
            if runes[i] == runes[i-1] {
                runes = append(runes[:i-1], runes[i+1:]...)
                judge = true
                break
            }
        }
        if !judge {
            break
        }
    }
    return string(runes)
}

不建议用暴力

正解：用栈
这种解法其实也是括号匹配这一类的题目。上个题目是相邻的括号，左括号的右括号匹配上了，进行删除，那这个题目就是相邻的字母如果相同就做一个消除的操作。这种消除规则的题，用栈都很合适。

来看这个题的模拟，看完你就知道为啥用栈了
我这里立马就可以总结了，扫描s的时候看和栈顶是否相等，相等就弹栈，不相等就入栈，最后遍历完了就把栈逆序输出就是结果。

func removeDuplicates(s string) string {
    stack := []byte{}
    for i:=0;i<len(s);i++{
        if len(stack)>0 && stack[len(stack)-1]==s[i]{
            stack=stack[:len(stack)-1]
        }else{
            stack=append(stack, s[i])
        }
    }

    return string(stack)
}

用go语言写就是有个好处，由于我是用数组模拟的，所以就没必要stack翻转输出结果了。

---

逆波兰表达式求值

知识补充：
逆波兰式是什么：就是后缀表达式。
波兰式是什么：前缀表达式。

前缀表达式，中缀表达式，后缀表达式是什么？
中缀表达式：就是我们平时习惯写的计算式a+b-c这种就叫中缀表达式，中缀表达式是我们比较习惯的计算方式，但是对于计算机来说，中缀表达式并不方便计算。对于计算机来说计算前缀表达式或后缀表达式的值就非常的简单。

前缀表达式：即表达式的运算符位于两个相应的操作数之前。
后缀表达式：即表达式的运算符位于两个相应的操作数之后。

因为我们编程是用计算机来计算。那么就会涉及将中缀表达式转后缀表达式，中缀表达式转前缀表达式。然后再使用对应的表达式的计算方法来计算结果。

中缀转后缀
我建议看这个视频，很清楚。只有一分钟。
https://www.bilibili.com/video/BV1xp4y1r7rc/?spm_id_from=333.337.search-card.all.click&vd_source=49ceaf0b94868131c32ccefb11e30e8f
要点我总结一下：
1.准备一个栈作为辅助，这个栈中只装操作符。
2.数字直接加入后缀表达式。
3.操作符入栈有优先级这个说法，这里我们分栈内字符和栈外字符。
（1）不管栈内或栈外，就是*/比±优先级高，栈外优先级比栈顶元素高就直接入栈。如果栈外操作符优先级比栈内低，那么栈内会一次进行比较然后出栈，直到能让栈外操作符入栈。
（2）（和）这个比较特殊：（直接入，比都不用比。栈外遇到），那么栈就必须进行弹栈，直到弹出（才停下来。注意这个配对的’）'不会进栈。
4.扫描完字符串了再把栈中的元素一次弹出加入后缀表达式

中缀转后缀还有个方法，就是将中缀表达式写成数的形式，然后后续遍历，就得到了后缀表达式。

中缀转前缀
1.初始化一个栈，拿来存运算符
2.对这个表达式从右往左扫描
3…遇到数字直接加入前缀表达式
4.遇到操作符：
（1）遇到’)‘直接入栈，遇到’(‘则开始进行弹栈，直到’)‘弹出为止，注意’(‘不入栈。
（2）遇到运算符，优先级的说法和上面中缀转后缀一样。栈内’)'优先级最低。
5…扫描完字符串了再把栈中的元素一次弹出加入前缀表达式

这里就来看后缀表达式求值，也就是逆波兰表达式求值。

看题解时的一点感悟：我们平时的中缀计算，我们要考虑括号的优先级。但是在后缀表达式计算中可以发现，居然没有括号。而且我们中缀转后缀的适合也是不把括号加入表达式，这样影响计算吗？回答是不会，因为计算机的计算就是顺序的扫描后缀表达式，它是顺序扫描，根本就不用管括号优先级。那么计算机如何顺序处理这个后缀表达式字符串，答案是用的栈。

这个题栈思路的体现就是遇到操作符，就做栈顶两个元素的合并操作。三个元素，两个操作数，一个操作符做一个计算然后再把计算结果加入栈中。非常适合做相邻字符的消除操作。

这里直接看后缀表达式计算思路：
扫描字符串，遇到数字直接加入栈中，遇到操作符，弹出栈顶两个元素，进行计算之后再压入栈中，直到扫描完毕，此时栈中剩下的那个元素就是计算结果。

import "strconv"
func evalRPN(tokens []string) int {
    stack:=[]int{}
    for _,v := range tokens{
        val,err:=strconv.Atoi(v)
        if err==nil{
            stack = append(stack,val)
        }else{
            num1,num2:=stack[len(stack)-2],stack[len(stack)-1]
            stack=stack[:len(stack)-2]
            if v == "+"{
                stack=append(stack,num1+num2)
            }else if v == "-"{
                stack=append(stack,num1-num2)
            }else if v == "*"{
                stack=append(stack,num1*num2)
            }else if v == "/"{
                stack=append(stack,num1/num2)
            }
        }
    }
    return stack[0]
}

这个代码写下来我还是出了一些语法上的错误，这里需要积累。

1.第一个问题是类型匹配的问题。v == “+”，我之前写的是v == ‘+’，我之前写的这个会报类型不匹配。后来我发现我的问题出在了哪里，func evalRPN(tokens []string) int，这个地方传的参数是字符串切片我真是服了。所以我for range得到的元素，那类型肯定是string，我当时以为是直接给了个字符串。所以这里用双引号就是"+"就是字符串类型。如果这个题给的字符串那么写’+'是没毛病的。

2.做的时候的一个问题，我怎么将字符转化成对应的整数。给的参数全是字符串，这里用的 strconv.Atoi(v)这个函数，这里必须要进行掌握。

strconv.Atoi 函数的转换原理主要基于解析和转换字符串中的数字字符。它从字符串的开始逐个字符地解析，将字符数字（如 ‘3’）转换为其对应的整数值（如 3），并构建出最终的整数值。

例如，对于字符串 “123”，strconv.Atoi 会这样处理：

解析 ‘1’，识别为整数 1。
解析 ‘2’，将当前整数乘以 10（变为 10）并加上 2，得到 12。
解析 ‘3’，再次乘以 10（变为 120）并加上 3，得到 123。
这个过程涉及将每个字符表示的数字从 ASCII 编码转换为其数值，并通过数学运算构造最终的整数结果。如果字符串中包含非数字字符或格式不正确，strconv.Atoi 将返回错误。

原理：ASCII 到数值的转换：对于字符串中的每个字符，strconv.Atoi 会将其从 ASCII 码转换为相应的数值。例如，字符 ‘0’ 到 ‘9’ 在 ASCII 表中对应的值是 48 到 57。要将这些字符转换为相应的整数 0 到 9，可以将字符的 ASCII 值减去 48。比如，ASCII 码为 51 的字符 ‘3’ 转换为整数 3 是通过计算 51 - 48 得到的。

数值构建：然后，strconv.Atoi 从字符串的左侧开始，逐个字符地计算整数值。对于每个新的数字字符，先将当前的数值乘以 10（向左移动一个数位），然后加上新字符代表的数值。例如，解析 “123” 时，开始是 1，然后是 1 * 10 + 2（得到 12），最后是 12 * 10 + 3（得到 123）。

了解完这个就感觉好做多了。注意它的参数很重要，一定要是string类型的。

3.一个衍生问题，单个字符’1’它的值应该是ASCII值，怎么转成我要的int值1.
要这么转化

char := '1'
num := char - '0'  // num 的类型是 int32 (rune)，值是 1