🕺作者: 主页
我的专栏 C语言从0到1 探秘C++ 数据结构从0到1 探秘Linux 😘欢迎关注:👍点赞🙌收藏✍️留言
🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的很重要,有问题可在评论区提出,感谢支持!!!
文章目录
- 实验一、DDA算法、Bresenham算法
- 一、实验目的及要求
- 二、实验设备
- 三、实验原理
- 四、实验方法与步骤
- 五、实验结果
- 六、结论
实验一、DDA算法、Bresenham算法
一、实验目的及要求
- 使用DDA算法画直线
- 使用Bresenham算法画直线和圆弧
二、实验设备
- Microsoft Visual Studio 2022
三、实验原理
- DDA算法(Digital Differential Analyzer): DDA算法是一种基于差分的算法,通过逐个增加x和y的步长来绘制直线。其基本原理是计算出两点之间的x和y的差值,然后根据斜率选择较大的差值来确定下一点的位置。
- Bresenham算法: Bresenham算法是一种整数算法,通过判断像素点到直线的距离来确定下一个像素点的位置。该算法通过利用递推关系式,避免了浮点数运算,提高了绘制速度。
四、实验方法与步骤
- 算法思想
- DDA算法:根据起点和终点的坐标,计算出x和y的增量,并根据斜率选择较大的增量来确定下一个像素点的位置。
- Bresenham算法:根据起点和终点的坐标,计算出dx和dy的差值,并根据差值来选择下一个像素点的位置。
- 算法步骤
- DDA算法:
- 计算出dx和dy的差值。
- 根据斜率选择较大的增量。
- 根据起点和增量计算下一个像素点的位置。
- 重复以上步骤,直到达到终点。
- Bresenham算法:
- 计算出dx和dy的差值。
- 判断斜率是否小于1,如果是则选择x方向为递增方向,否则选择y方向为递增方向。
- 根据判断结果选择递增方向,并计算初始决策参数。
- 循环计算下一个像素点的位置,并更新决策参数。
- 重复以上步骤,直到达到终点。
- 代码
- DDA算法画直线
void LineDDA(int x0, int y0, int x1, int y1)
{
// 初始化变量
int x;
int dy, dx;
int y;
float k;
// 计算斜率和增量
dx = x1 - x0;
dy = y1 - y0;
k = (float)dy / dx; // 计算斜率
y = y0; // 初始化y坐标为起始点y坐标
// 设置绘制点的颜色和大小
glColor3f(0.0f, 0.0f, 0.0f); // 将线条颜色设置为黑色
glPointSize(1);
// 使用逐点递增算法绘制直线
for (x = x0; x <= x1; x++) {
glBegin(GL_POINTS); // 开始绘制一个点
glVertex2i(x, (int)(y + 0.5)); // 绘制当前像素点
glEnd(); // 结束绘制点
y += k; // 根据斜率递增y坐标
}
// 强制刷新缓冲区,执行绘制命令
glFlush();
}
- Bresenham算法画直线
void Line(int x0, int y0, int x1, int y1)
{
// 判断斜率绝对值是否大于1,以确定直线是陡峭还是平缓
bool steep = abs(y1 - y0) > abs(x1 - x0);
// 如果是陡峭的直线,则交换x和y的坐标值
if (steep) {
swap(x0, y0);
swap(x1, y1);
}
// 确保x0 < x1
if (x0 > x1) {
swap(x0, x1);
swap(y0, y1);
}
// 计算直线斜率的绝对值
int dx = x1 - x0;
int dy = abs(y1 - y0);
// 初始化误差值和y的增量
int error = dx / 2;
int ystep = (y0 < y1) ? 1 : -1;
int y = y0;
// 设置绘制颜色为红色
glColor3f(1.0f, 0.0f, 0.0f);
// 使用 Bresenham 算法绘制直线
for (int x = x0; x <= x1; x++) {
glBegin(GL_POINTS);
if (steep) {
glVertex2i(y, x);
}
else {
glVertex2i(x, y);
}
glEnd();
error -= dy;
if (error < 0) {
y += ystep;
error += dx;
}
}
}
- Bresenham算法画圆
void CirclePoints(int cx, int cy, int x, int y) {
glBegin(GL_POINTS);
glVertex2i(cx + x, cy + y);
glVertex2i(cx - x, cy + y);
glVertex2i(cx + x, cy - y);
glVertex2i(cx - x, cy - y);
glVertex2i(cx + y, cy + x);
glVertex2i(cx - y, cy + x);
glVertex2i(cx + y, cy - x);
glVertex2i(cx - y, cy - x);
glEnd();
}
void DrawCircle(int cx, int cy, int radius, bool drawFullCircle = true) {
int x = 0;
int y = radius;
int d = 3 - 2 * radius;
glColor3f(1.0f, 0.0f, 0.0f);
while (x <= y) {
if (drawFullCircle) {
CirclePoints(cx, cy, x, y);
}
else {
// 如果只画圆弧,可以在这里加入逻辑来决定哪些点应该被画出来
glBegin(GL_POINTS);
glVertex2i(cx + x, cy + y); // 仅示例:画1/8圆弧
glEnd();
}
if (d < 0) {
d += 4 * x + 6;
}
else {
d += 4 * (x - y) + 10;
y--;
}
x++;
}
}
五、实验结果
- DDA算法画直线

- Bresenham算法画线
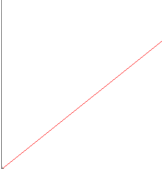
- Bresenham算法画圆

六、结论
- DDA算法和Bresenham算法都是用于绘制直线的算法,它们各有特点:
- DDA算法(Digital Differential Analyzer)是一种基于差分的算法,通过逐个增加x和y的步长来绘制直线。它的优点在于简单易懂,但由于需要进行浮点数运算,因此在绘制速度上相对较慢。
- Bresenham算法是一种整数算法,通过判断像素点到直线的距离来确定下一个像素点的位置,避免了浮点数运算,提高了绘制速度。因此,Bresenham算法在绘制直线时具有更高的效率。
- 在绘制圆弧时,Bresenham算法同样展现了其优势,通过使用整数计算和递推关系式,能够高效地绘制圆形和圆弧。
因此,根据本次实验结果,可以得出结论:在绘制直线和圆弧时,Bresenham算法相比DDA算法具有更高的效率和精确度,特别是在涉及大量像素绘制的情况下,Bresenham算法更为优越。