目录
初识聚类算法
聚类算法实现流程
模型评估
算法优化
特征降维
探究用户对物品类别的喜好细分(实操)
初识聚类算法
聚类算法是一种无监督学习方法,用于将数据集中的对象按照相似性分组。它旨在发现数据中的内在结构和模式,将具有相似特征的数据点聚集到同一组中,并将不同组之间的差异最大化。使用不同的聚类法则,产生的聚类结果也不尽相同:

聚类算法在现实中的应用:
1)用户画像,广告推荐,DataSegmentation,搜索引l擎的流量推荐,恶意流量识别
2)基于位置信息的商业推送,新闻聚类,筛选排序
3)图像分割,降维,识别;离群点检测;信用卡异常消费;发掘相同功能的基因片段
聚类算法是无监督的学习算法,而分类算法属于监督的学习算法。
接下来我们随机创建不同二维数据集作为训练集,并结合k-means算法将其聚类,尝试分别聚类不同数量的,并观察聚类效果:
首先我们先导入相关使用的第三方库:
import matplotlib.pyplot as plt
from sklearn.datasets._samples_generator import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import calinski_harabasz_score# n_clusters:开始的聚类中心数量,省值=8,生成的聚类数,即产生的质心(centroids)数。
# estimator.fit_predict(x): 计算聚类心并预测每个样本属于哪个类别,相当于先调用fitx),然后再调用predict(x)
# 创建数据
X, Y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]], cluster_std=[0.4, 0.2, 0.2, 0.2], random_state=9)
# 可视化展示
plt.scatter(X[:, 0], X[:, 1], marker="o")
plt.show()最终呈现的效果如下所示:
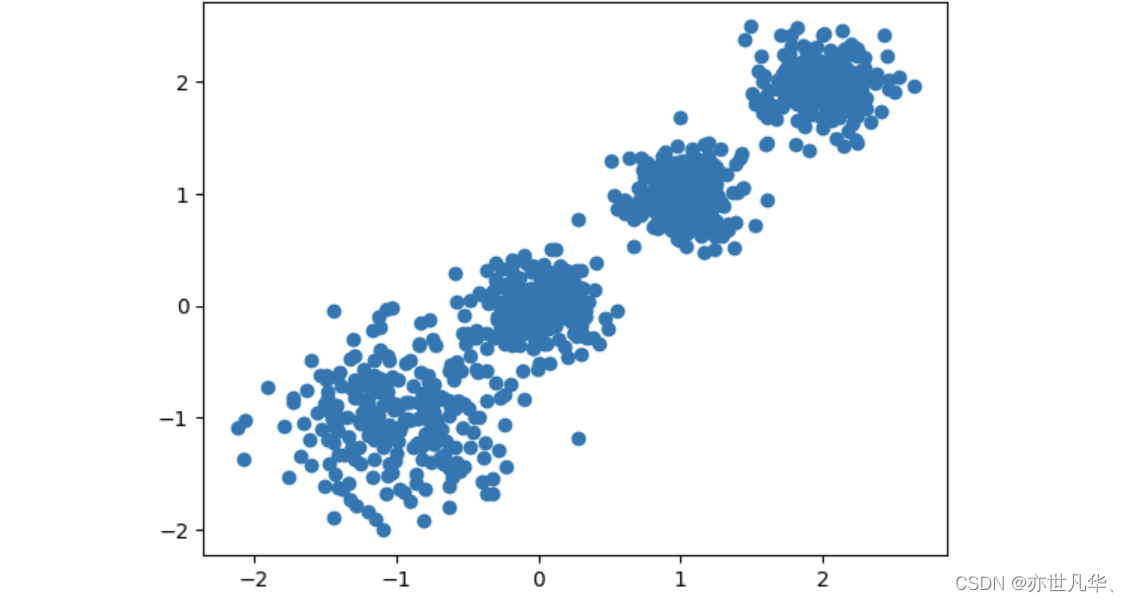
接下来这段代码使用了K-means聚类算法对给定数据集X进行聚类,聚成两个簇:
# KMeans是Scikit-learn库中的K-means聚类算法实现;
# n_clusters=2表示要将数据划分为2个簇;
# n_init=10表示运行算法的次数,以选择最佳结果;
# random_state=9表示随机数生成器的种子,确保结果可以被重复。
# kmeans训练 聚类=2
y_pre = KMeans(n_clusters=2, n_init=10, random_state=9).fit_predict(X)
# 可视化展示
plt.scatter(X[:, 0], X[:, 1], c=y_pre)
plt.show()
# 用ch_scale查看最后效果
print(calinski_harabasz_score(X, y_pre))呈现的效果如下所示:
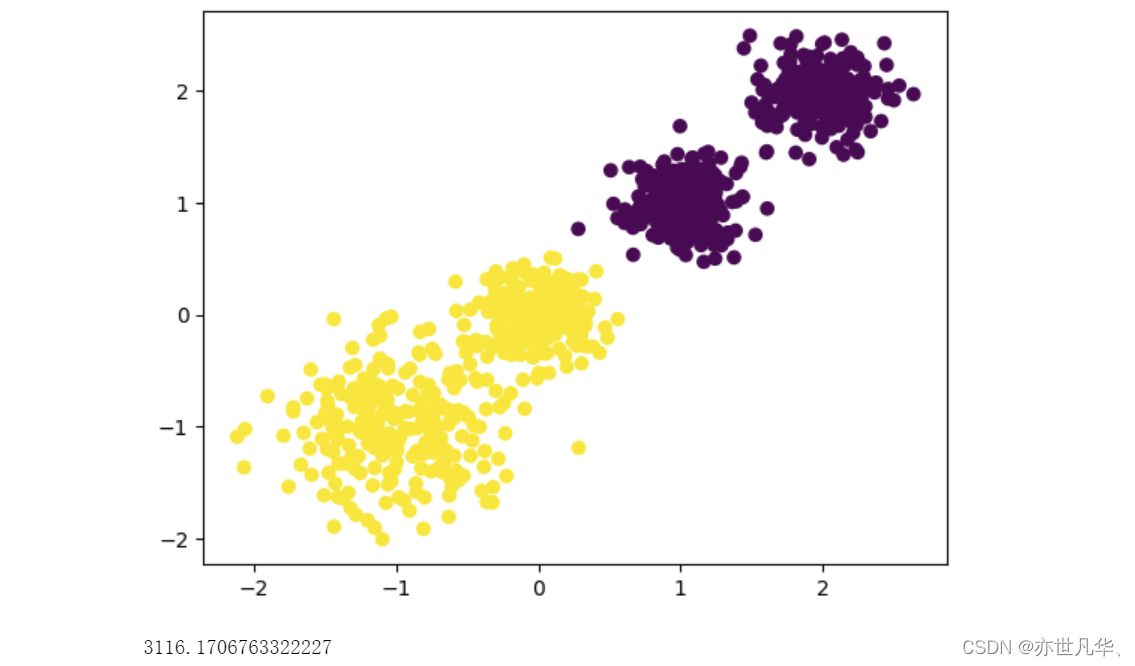
接下来我们改变聚类中心的数量得到的结果如下所示:

聚类算法实现流程
根据上面的案例,我们了解到 K-means 聚类步骤如下:
1)随机设置K个特征空间内的点作为初始的聚类中心

2)对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
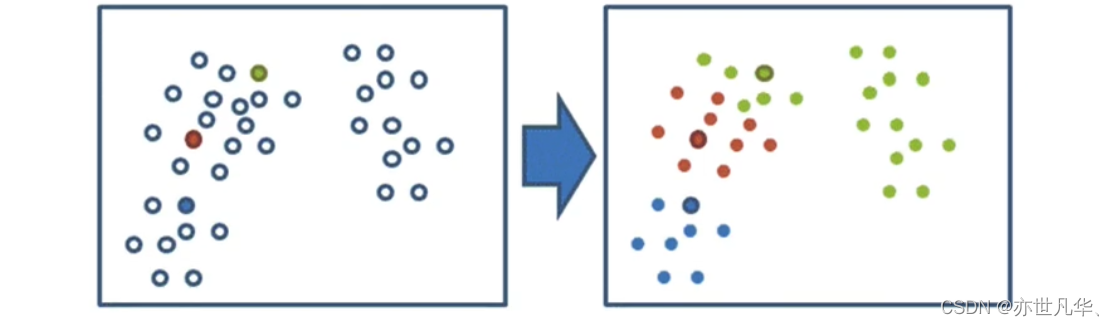
3)接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值),如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程:

接下来通过动态图进行演示实现上面的过程:

接下来通过一个案例数据来进行演示:
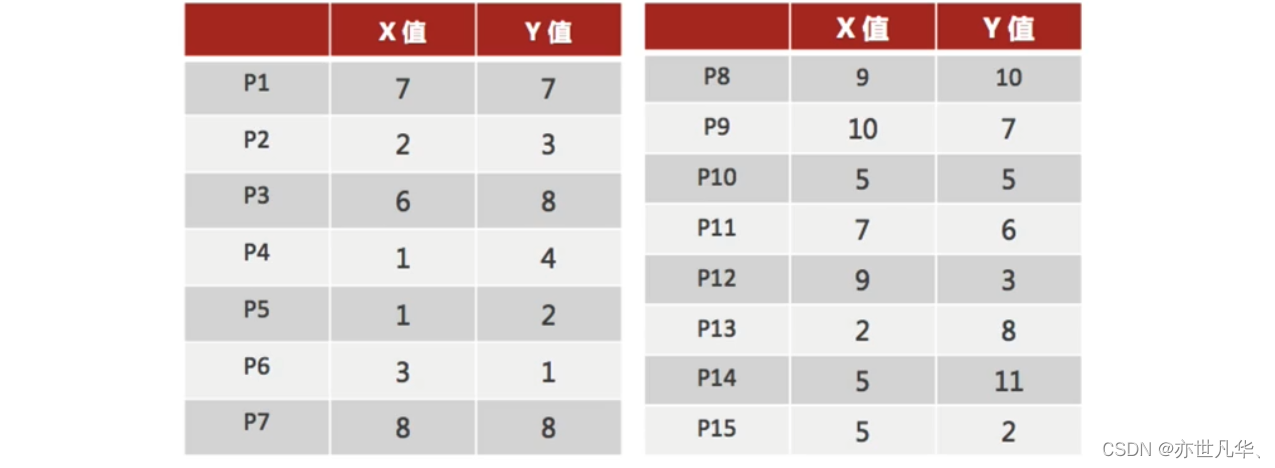
1)随机设置K个特征空间内的点作为初始的聚类中心(本案例中设置p1和p2):
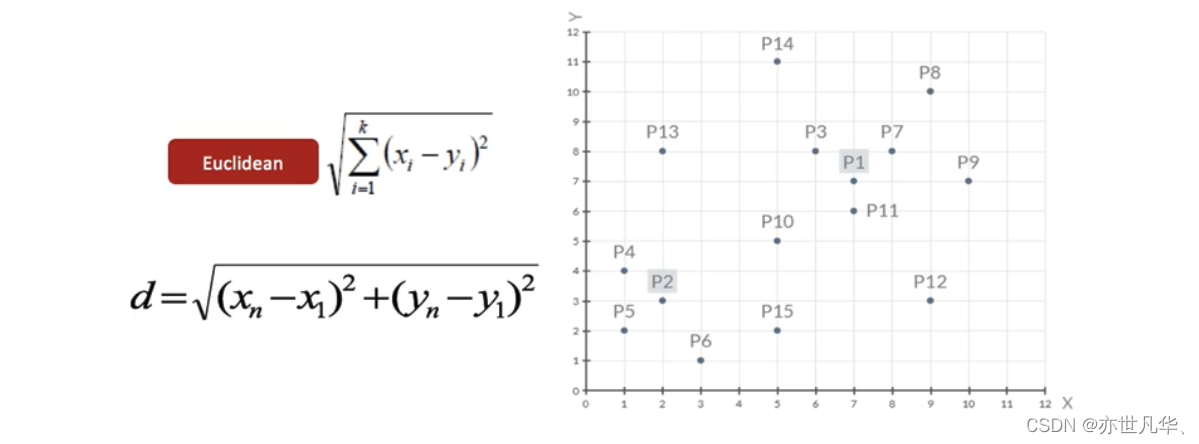
2)对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别:
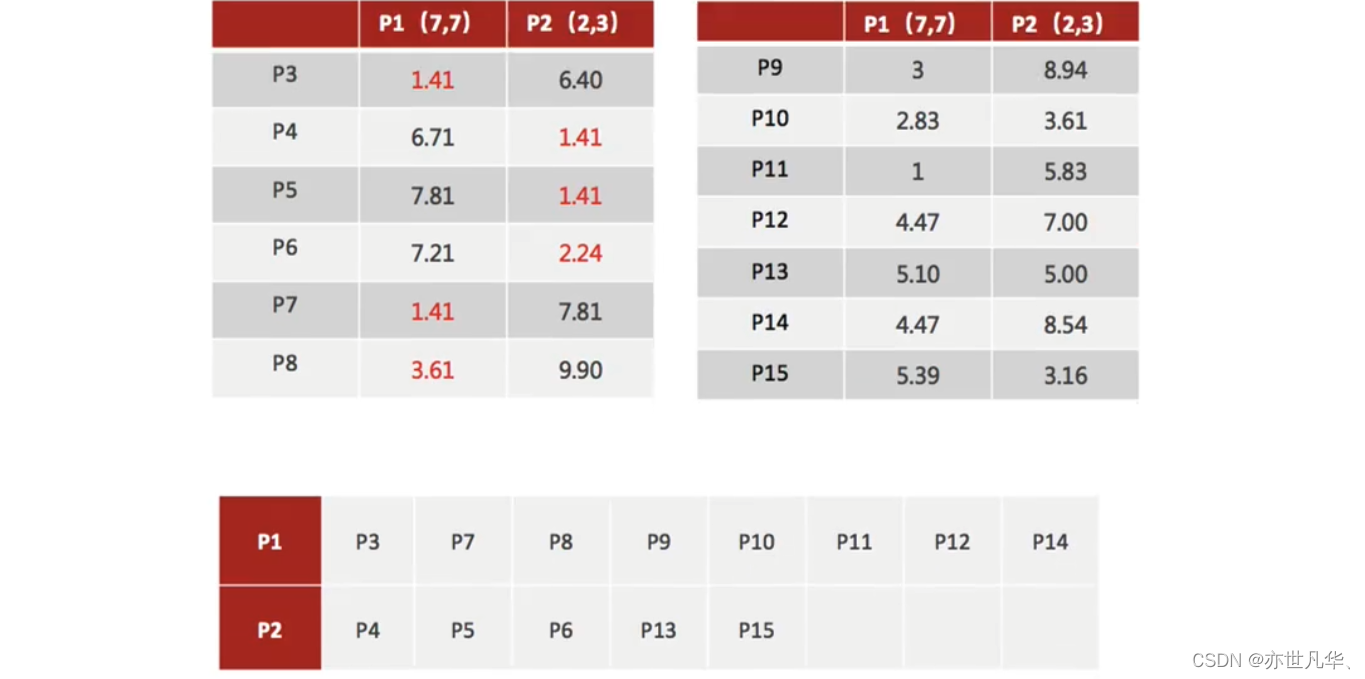
3)接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值):
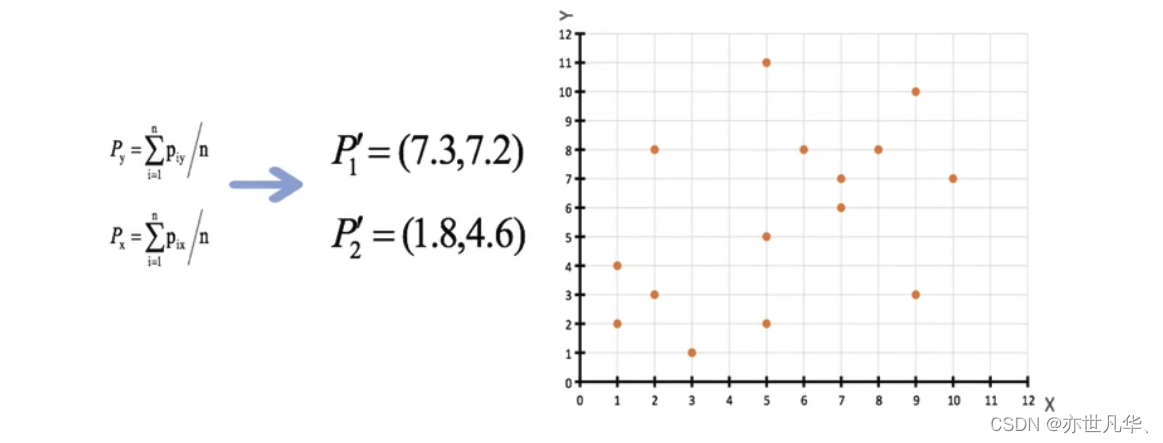
4)如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程【经过判断,需要重复上述步骤,开始新一轮迭代】
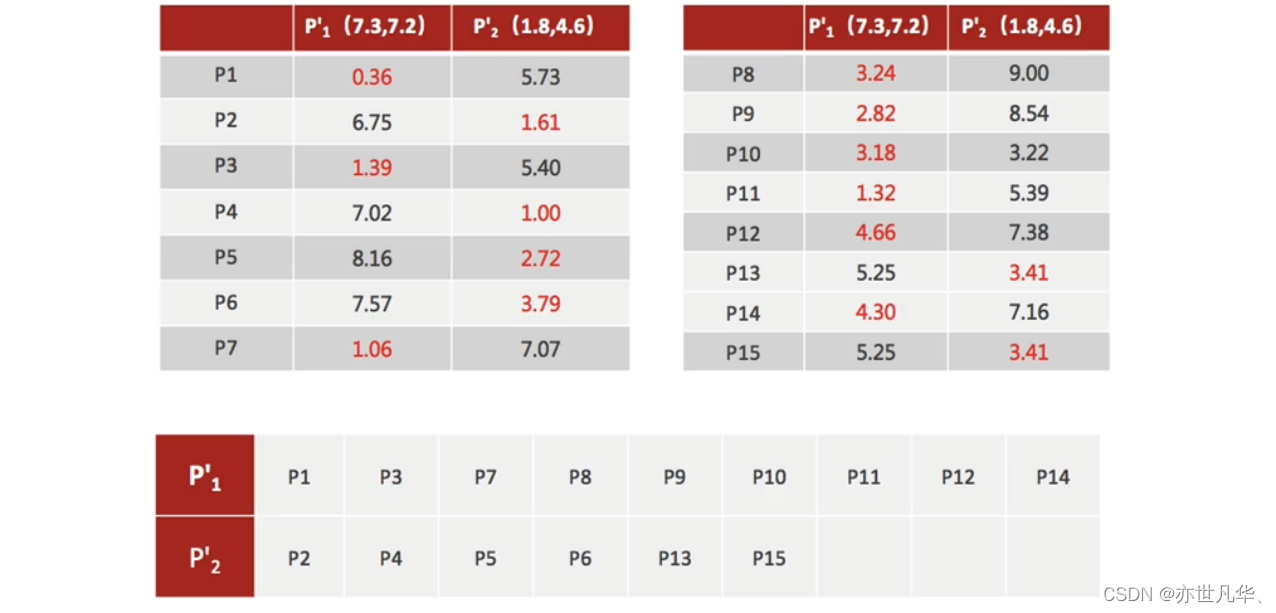
5)当每次迭代结果不变时,认为算法收敛,聚类完成,K-Means一定会停下,不可能陷入一直选质心的过程。

K-means聚类实现流程总结:
1)事先确定常数K,常数K意味着最终的聚类类别数;
2)随机选定初始点为质心,并通过计算每一个样本与质心之间的相似度(这里为欧式距离),将样本点归到最相似的类中,
3)接着,重新计算每个类的质心(即为类中心),重复这样的过程,直到质心不再改变,
4)最终就确定了每个样本所属的类别以及每个类的质心。
注意:由于每次都要计算所有的样本与每一个质心之间的相似度,故在大规模的数据集上,K-Means算法的收敛速度比较慢。
K-means聚类算法优缺点:
优点:原理简单(靠近中心点),实现容易;聚类效果中上 (依赖K的选择);空间复杂度o(N),时间复杂度o(IKN)
缺点:对离群点,噪声敏感(中心点易偏移);很难发现大小差别很大的簇及进行增量计算;结果不一定是全局最优,只能保证局部最优(与K的个数及初值选取有关)
模型评估
在聚类算法中,模型评估是通过一些内部或外部指标来衡量聚类质量的过程。这些指标可以帮助我们了解聚类模型对数据集的可靠性和有效性。在聚类算法中,有一些常用的模型评估指标,包括SSE(Sum of Squared Errors,误差平方和)、"肘"部法(Elbow Method)、轮廓系数(Silhouette Coefficient,SC)和Calinski-Harabasz指标(CH)。这些指标可以帮助我们选择最佳的聚类数量和评估聚类模型的质量。但需要注意的是,它们仅供参考,具体选择还需结合实际问题和经验。以下是模型评估指数介绍:
SSE:SSE衡量了每个数据点到其所属簇的质心的距离的平方和。SSE越小,表示数据点越接近其所属簇的质心,聚类效果越好。然而,SSE不能直接用于比较不同聚类数量的模型,因为随着聚类数量的增加,SSE通常会减小。
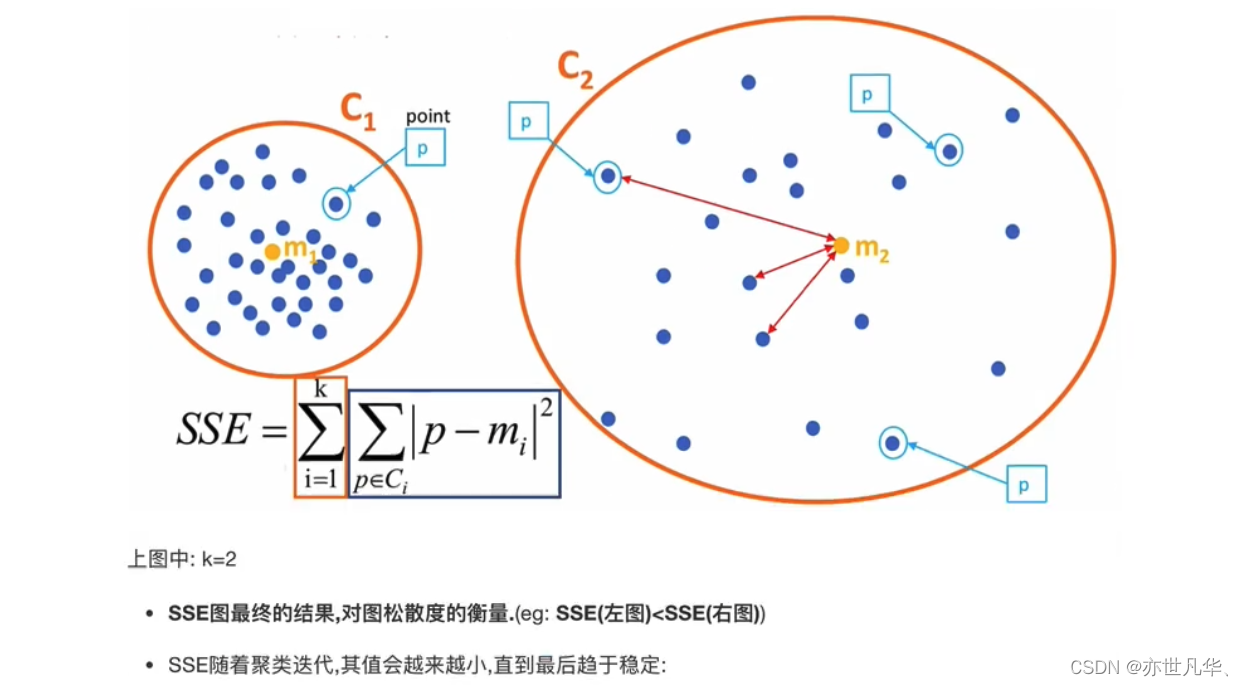
"肘"部法:肘部法是一种通过绘制聚类数量与对应的SSE之间的关系图来选择最佳聚类数量的方法。图形通常呈现出一个弯曲的曲线,在聚类数量逐渐增加时,SSE下降的速度会变缓。选择"肘"部的聚类数量,即找到SSE曲线的拐点,可以认为是最佳的聚类数量。

SC轮廓系数:轮廓系数是一种用于评估聚类结果的紧密度和分离度的指标。它计算每个数据点的轮廓系数,该系数考虑了数据点与其所属簇的距离以及与其他簇的距离。轮廓系数的取值范围在[-1, 1]之间,越接近1表示聚类结果越好。
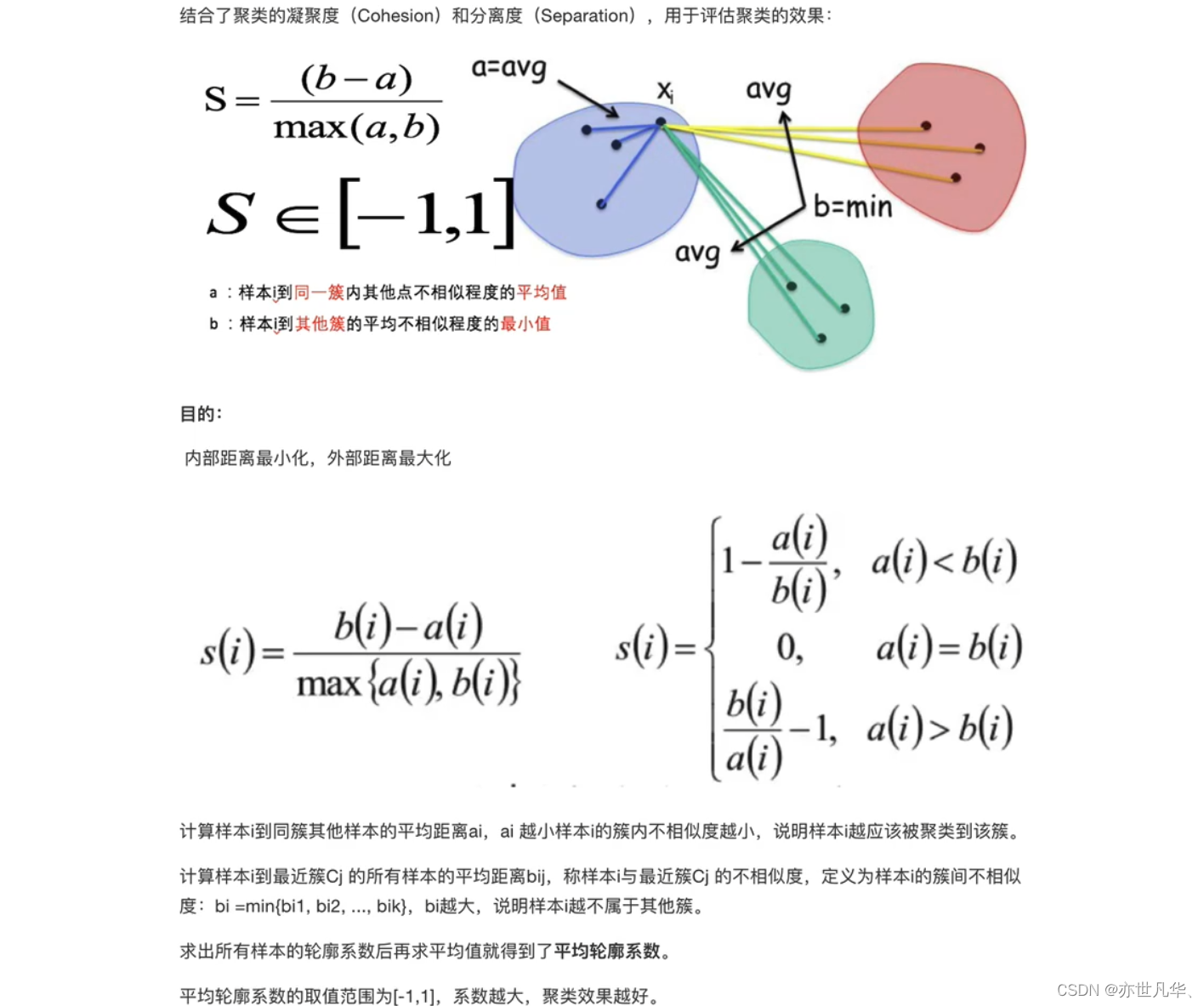
CH系数:Calinski-Harabasz指标是另一种用于评估聚类结果的指标,它基于簇内方差和簇间方差的比率。较高的Calinski-Harabasz指标表示聚类结果具有较好的紧密度和分离度。


算法优化
通过算法优化,可以改善聚类算法的性能、稳定性和准确性,以更好地发现数据中的结构和模式。以下是几种算法优化的简介:
Canopy算法:将数据点分配到不同的组中,可以有效减少K-means算法计算负担。同时,Canopy算法还可以为K-means算法提供初始质心,并且在保证聚类效果的情况下,可以通过调整T1和T2的值来控制聚类数量。
在给定的所有点中选择其中一个点当作质心,以当前质点为圆心t1为半径画圆,在圆内的点标记为黄色,再以当前质点为圆心t2为半径画圆,把落在圆环内的点加粗,如下:
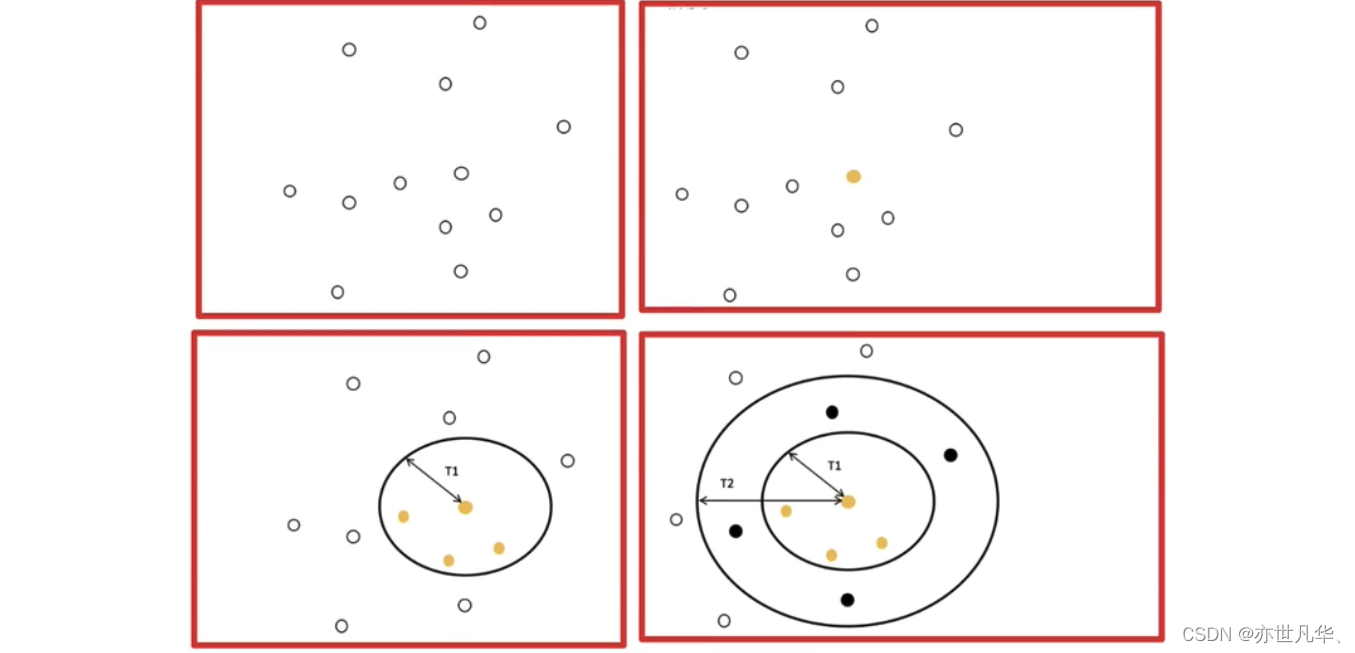
接下来把圆外的点随机选一个作为圆心继续画圆,操作步骤与上面类似,直到把所有点都包括进去

Canopy算法的优缺点:
优点:
1)Kmeans对噪声抗干扰较弱,通过Canopy对比,将较小的NumPoint的Cluster直接去掉有利于抗干扰。
2)Canopy选择出来的每个Canopy的centerPoint作为K会更精确。
3)只是针对每个Canopy的内做Kmeans聚类,减少相似计算的数量。
缺点:
1)算法中T1、T2的确定问题,依旧可能落入局部最优解
K-means++算法:通过选择合适的初始质心,可以加速K-means算法的收敛速度,减少聚类结果受到初始值的影响,并且在一定程度上提高聚类效果。

如下图中,如果第一个质心选择在圆心,那么最优可能选择到的下一个点在P(A)这个区域(根据颜色进行划分):
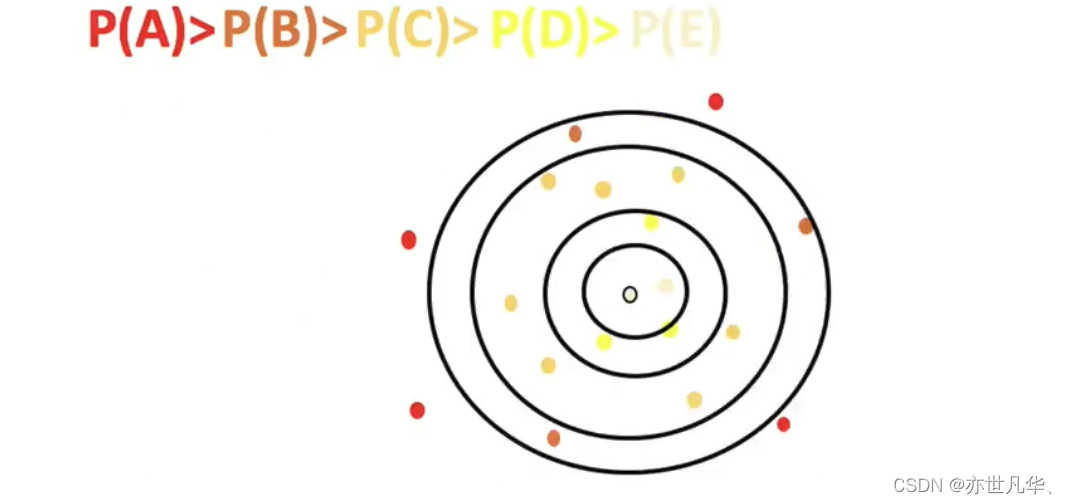
二分K-means算法:通过动态地选择聚类数量和质心,可以避免K-means算法陷入局部最优解,并且在一定程度上提高聚类效果。
实现流程:
1)所有点作为一个簇。
2)将该簇一分为二。
3)择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。
4)以此进行下去,直到簇的数目等于用户给定的数目k为止。
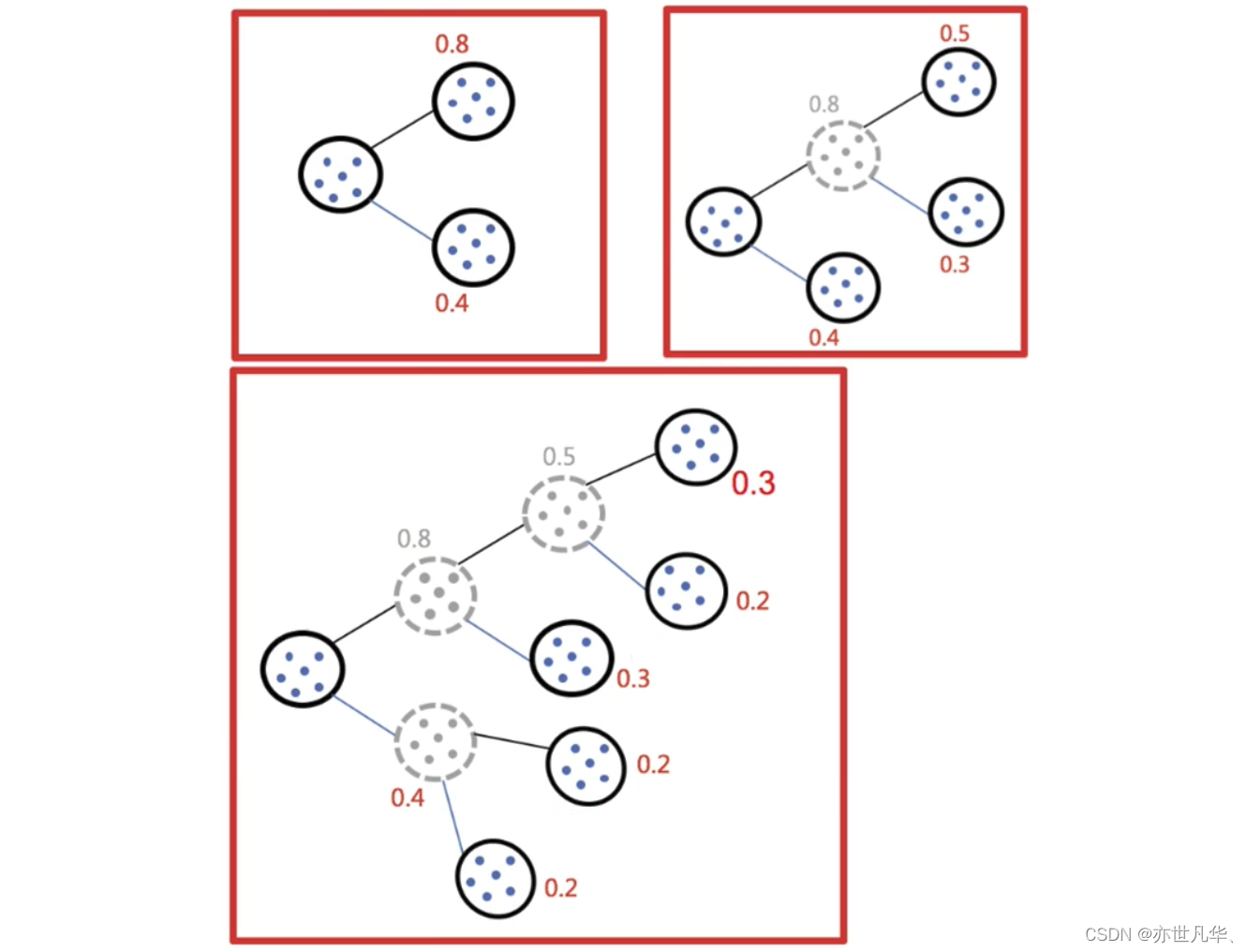
因为聚类的误差平方和能够衡量聚类性能,该值越小表示数据点越接近于他们的质心,聚类效果就越好。所以需要对误差平方和最大的簇进行再一次划分,因为误差平方和越大,表示该簇聚类效果越不好,越有可能是多个簇被当成了一个簇,所以我们首先需要对这个簇进行划分。
二分K均值算法可以加速K-means算法的执行速度,因为它的相似度计算少了并且不受初始化问题的影响,因为这里不存在随机点的选取,且每一步都保证了误差最小。
K-medoids算法:通过选择代表性对象作为质心,可以避免出现非数据点的质心,从而提高聚类结果的可解释性。同时,选择medoid作为质心可以减少聚类结果受到异常值的影响。

特征降维
特征降维是指通过某种数学变换或算法,将原始数据集中的高维特征转化为低维表示的过程。在机器学习和数据分析中,特征降维可以帮助减少数据集的维度,提取最具代表性的特征,去除冗余信息,并且有助于可视化和理解数据。
降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程:

降维有两种方式 :特征选择和主成分分析(特征提取的方式),以下进行讲解:
特征选择:数据中包含余或无关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征。其对应的方法如下:

低方差特征过滤:通过如下代码进行演示:
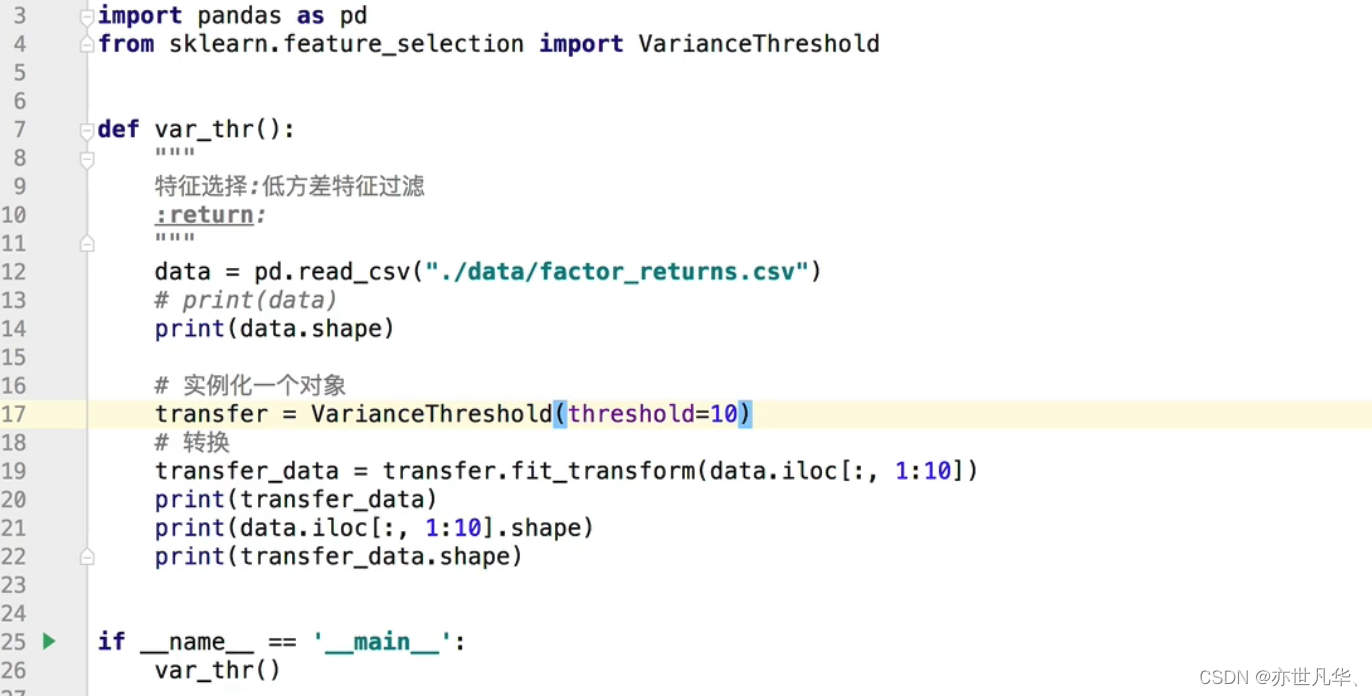
最终呈现的效果如下:

其相关系数的主要实现方式有 皮尔逊相关系数和斯皮尔曼相关系数:
皮尔逊相关系数:反映变量之间相关关系密切程度的统计指标

其案例实现的代码如下:
from scipy.stats import pearsonr
def pea_demo():
# 准备数据
x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9]
x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5]
# 判断
ret = pearsonr(x1, x2)
print("皮尔逊相关系数的结果是:\n", ret)
pea_demo()最终呈现的效果如下所示:

斯皮尔曼相关系数:反映变量之间相关关系密切程度的统计指标
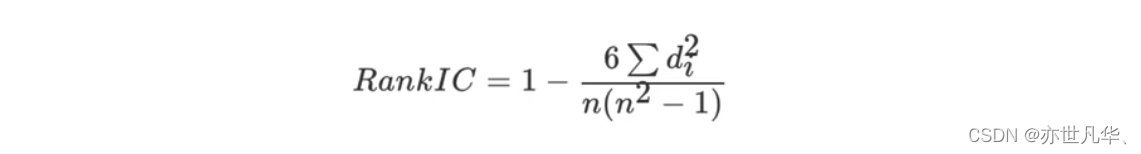
其案例实现的代码如下:
from scipy.stats import spearmanr
def pea_demo():
# 准备数据
x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9]
x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5]
# 判断
ret = spearmanr(x1, x2)
print("斯皮尔曼相关系数的结果是:\n", ret)
pea_demo()最终呈现的效果如下所示:

主成分分析:
定义:高维数据转化为低维数据的过程,在此过程中可能会舍弃原有数据、创造新的变量。
作用:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
应用:回归分析或者聚类分析当中。
这里拿一个简单的数据进行测试一下:
from sklearn.decomposition import PCA
def pca_demo():
data = [[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]]
# pca小数保留百分比
transfer = PCA(n_components=0.9)
trans_data = transfer.fit_transform(data)
print("保留0.9的数据最后维度为: \n", trans_data)
# pca小数保留百分比
transfer = PCA(n_components=3)
trans_data = transfer.fit_transform(data)
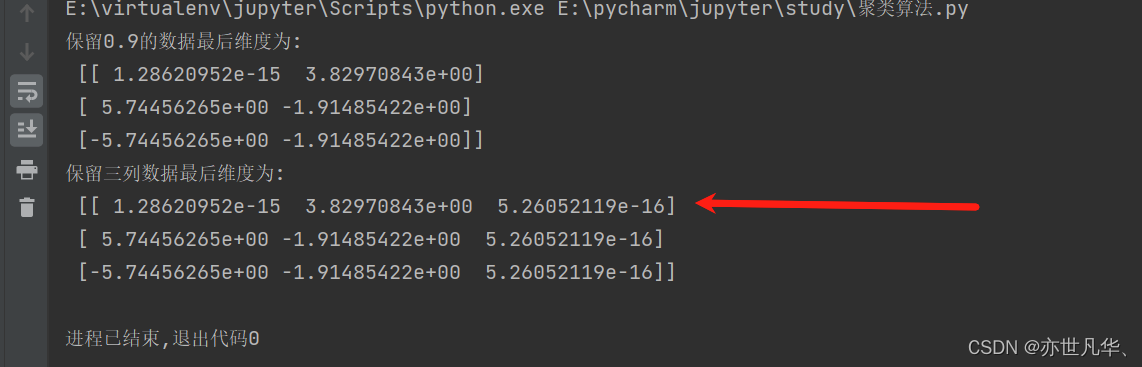
print("保留三列数据最后维度为: \n", trans_data)
pca_demo()最终呈现的效果如下所示:
探究用户对物品类别的喜好细分(实操)
接下来通过kaggle平台中的:竞赛 中的一道题目:应用 PCA 和 K-means 实现用户对物品类别的喜好细分划分,来加强我们聚类算法的学习:
数据集当中对应的数据如下:

根据竞赛提供的信息:

得到的最终结果需求是:

接下来我们开始正式对竞赛题目开始操作,以下是项目操作的具体步骤:
获取数据:

数据基本处理:
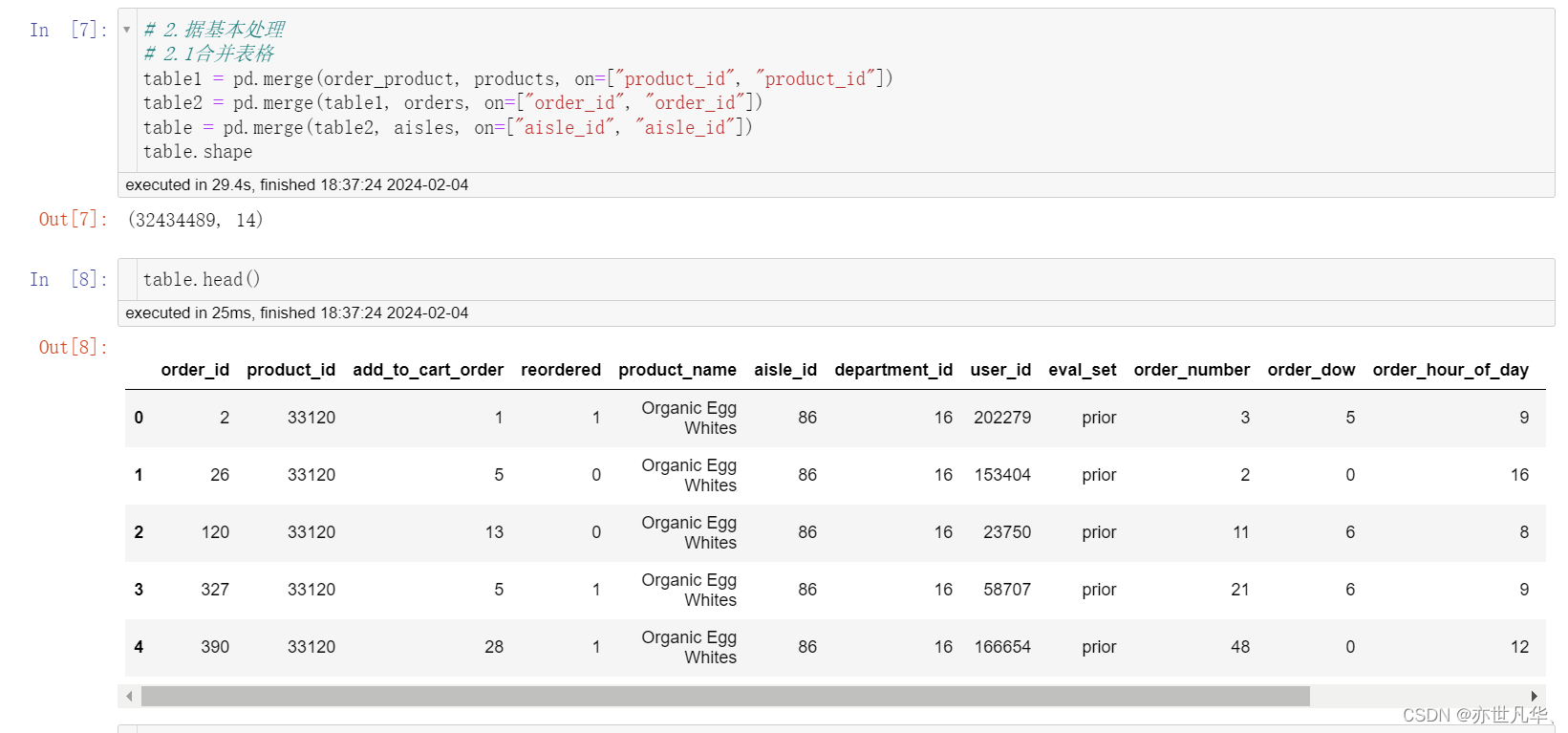
交叉表(Cross Tabulations)是一种常用的分类汇总表格,用于频数分布统计,主要价值在于描述了变量间关系的深刻含义。它可以计算两个(或更多)因子的简单交叉表。默认情况下,它会计算因子的频率表,除非传递了值数组和聚合函数。
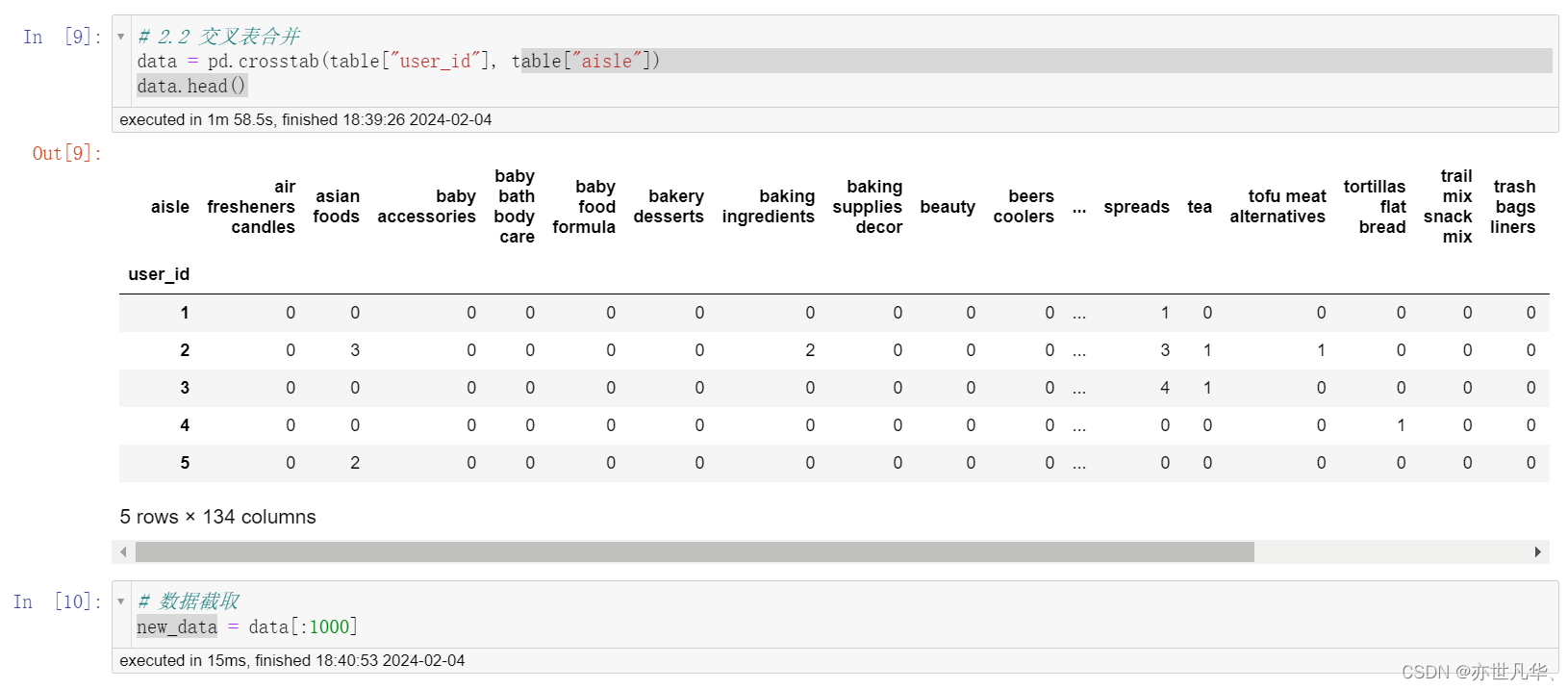
特征工程:

机器学习(K-means聚类):
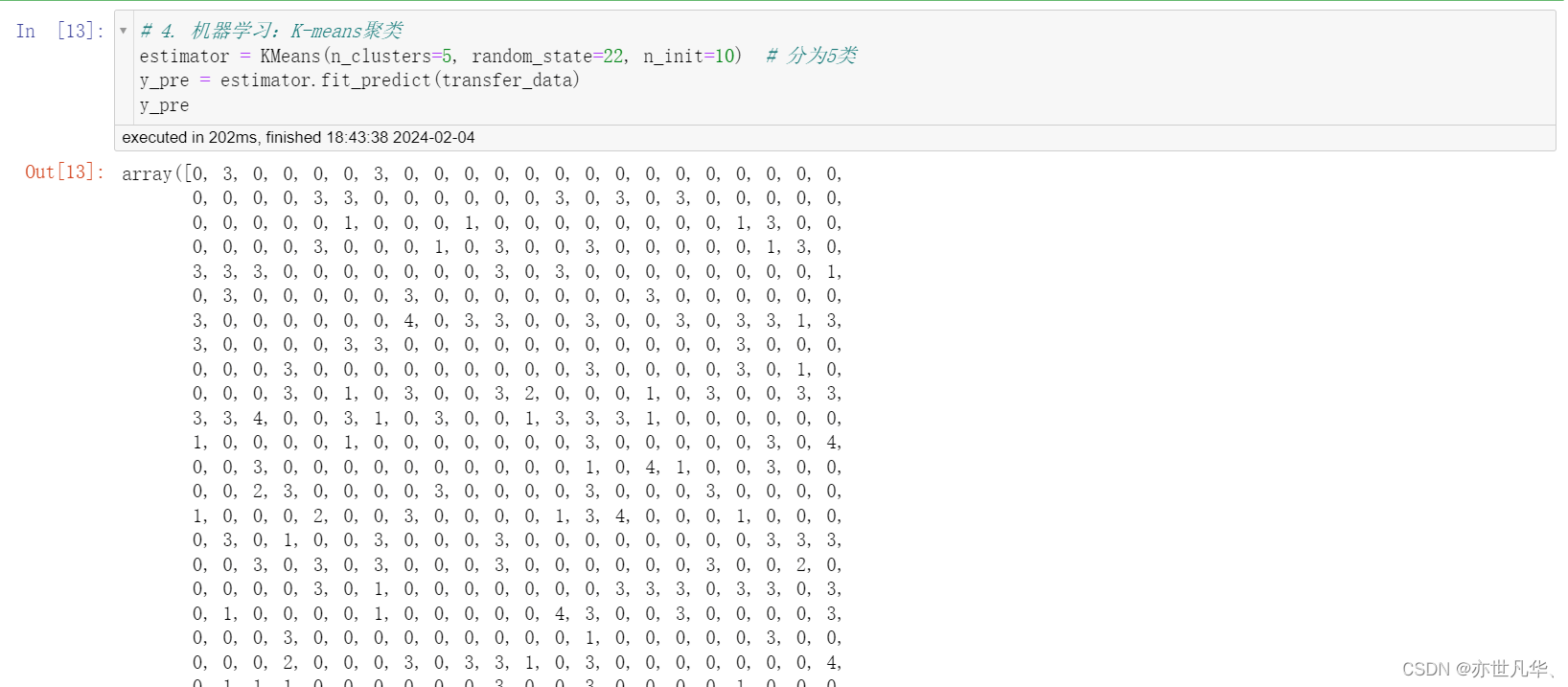
模型评估: