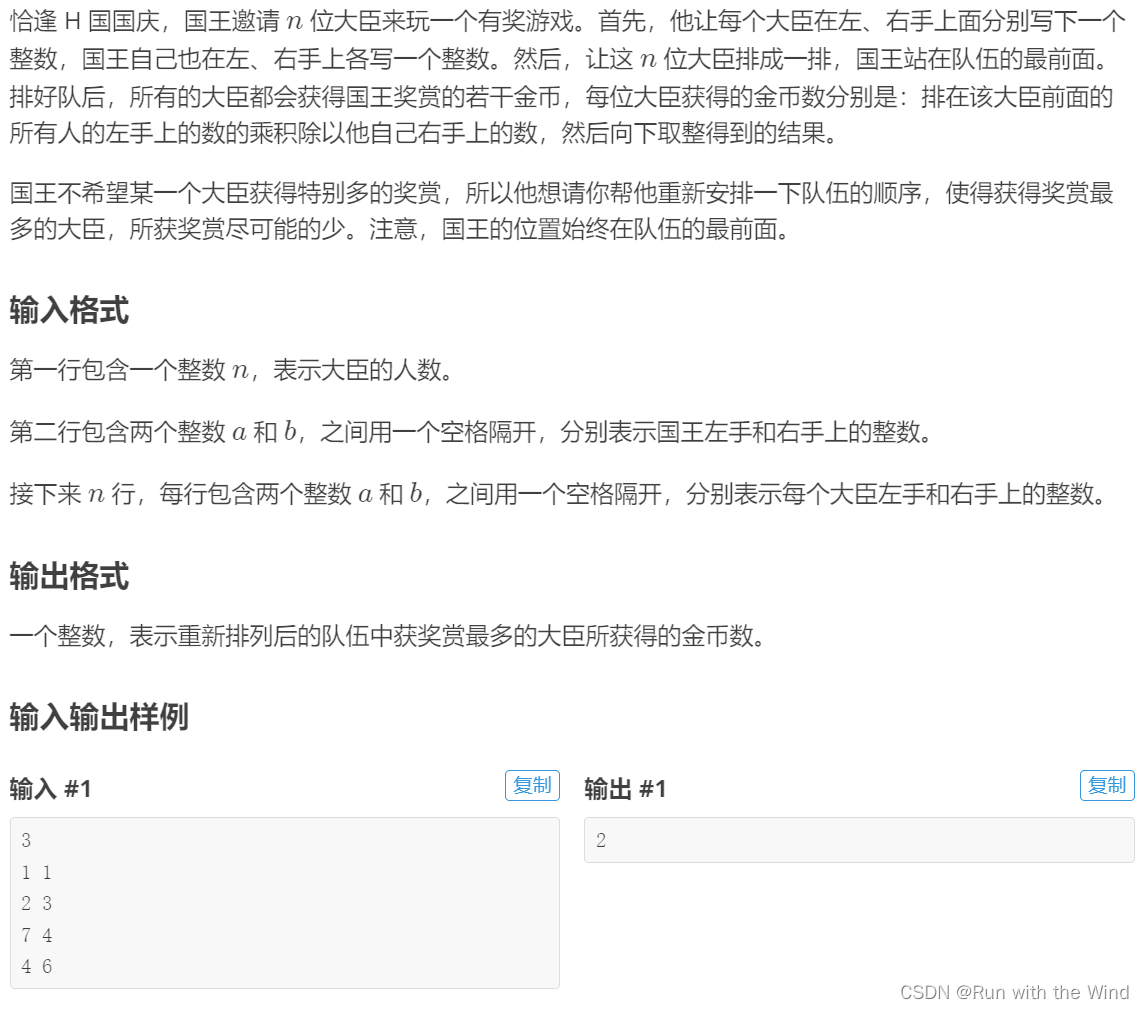
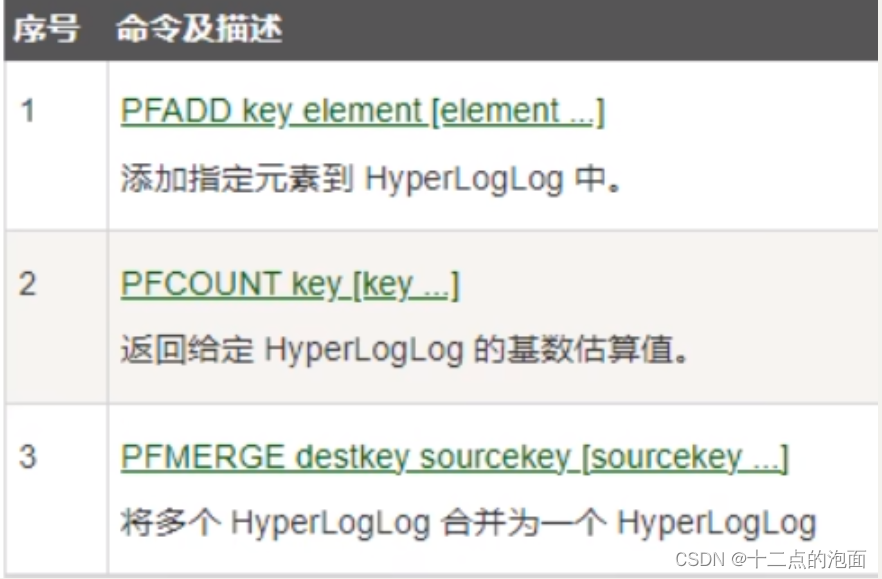
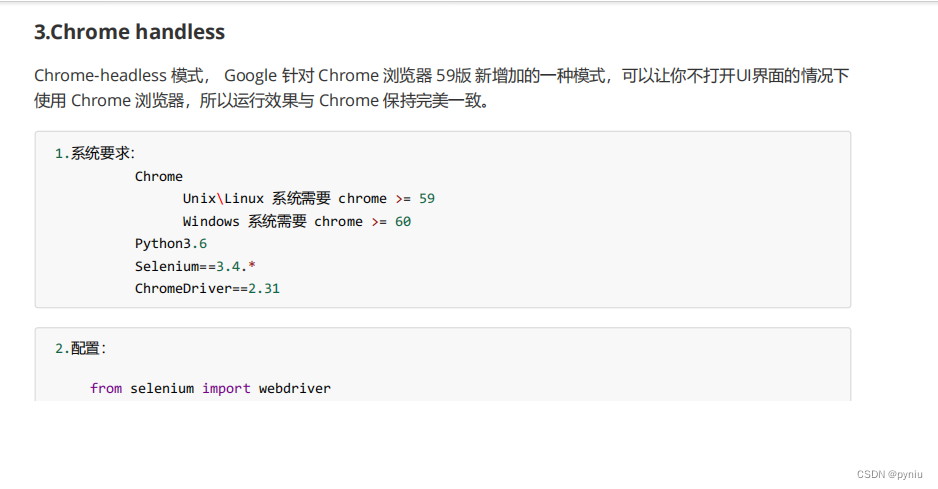
题目描述

---

题目思路

涉及排列组合求最优解问题，数据大考虑是否满足某种贪心策略。

假设不除以右手的数字，那么获得金币数量最多的显然为最后一个人。左手数字最大的应排在最后一位。在右手有数字的情况下，不妨也尝试从最后一个人开始排。

假设最后一个为第个人（国王为第0个），他左手和右手上的数字分别为和，他获得的金币为。则：

①  

假设将他和第一个大臣交换位置，则最后一个获得的金币变成：
②  

将①式与②式相除，得：
③  

要使最后一个人获得的金币数尽可能少，应使，则应尽可能大。

现在我们已经知道了使最后一个获得金币最少的策略。接下来需证明所有人都用这种策略就能使最大金币数最小。假设最后一个人可能获得金币的数量有种，分别为，分别对应第个人在最后一个位置上时获得金币数。倒数第二个人可能获得金币的数量有种，分别为，因为已经有一个人排到了最后一个位置上。

易证：

因此，每次应选取中最小的那一个，这样剩余的在转化成时值都会减小，按此策略选择出的最大金币数也是最小的。

还有一个细节，当两个的值相同的时候应先排哪个？
当，设先排，则：

两式相除得：

可以看出后排获得得金币数，为了使后一个获得的金币数尽可能少，故两个的值相同的时候应先排更高的。

---

我的代码

为了求的最大值，需要在执行贪心策略的过程中使用排序算法，由于排序中涉及两个变量，故采用map容器排序，时间复杂度为。由于部分数据范围需要高精度算法。高精度部分尚未实现。

#include <iostream>
#include <algorithm>
#include <map>
#include <set>
using namespace std;
typedef multiset<int> s;
typedef pair<int, s> p;
map<int, s> m;
map<int, s>::iterator it;
multiset<int>::iterator it2;
int a[1001];
int b[1001];
int main() {
	int n;
	//快速排序
	cin >> n;
	cin >> a[0] >> b[0];
	for (int i = 1; i <= n; i++)
	{
		s S;
		cin >> a[i] >> b[i];
		S.insert(a[i]);
		//向map容器插入数据
		pair<map<int, s>::iterator, bool> flag = m.insert(p(a[i] * b[i], S));
		//检查元素是否冲突(ab相等)
		if (!flag.second) {
			s S2((*flag.first).second);
			S2.insert(a[i]);
			m.erase(flag.first);
			m.insert(p(a[i] * b[i], S2));
		}
	}
	//执行贪心
	long long mult = a[0];
	long long ans = 0;
	for (it = m.begin(); it != m.end(); it++) {
		s S((*it).second);
		for (it2 = S.begin(); it2 != S.end(); it2++) {
			long long L = *it2;
			//cout << L;
			long long R = (*it).first / L;
			//cout << R;
			ans = max(ans, (mult / R));
			mult = mult * L;
		}
	}
	cout << ans<< endl;
	return 0;
}