本节和前一节 【现代机器人学】学习笔记八：轨迹生成 不同，侧重于避障的内容。

有一些我认为的重要的基本的概念：

1.路径规划是一个纯几何问题，寻找一条无碰撞路径，不涉及动力学和时间相关内容。因此路径规划是运动规划的子问题，运动规划是要涉及到动力学、时间、运动约束等内容的。
2.控制输入的总数小于自由度数目，机器人无法跟踪多条路径。
3.如果解存在，运动规划能在有限时间找到解，并且在没有解的情况下报告错误，认为 该运动规划算法是完整的。
4. 对问题进行离散化表示，能在分辨率层级上找到解，称 算法在分辨率层级上是完整的。
5.在时间趋近于无穷大的时候，找到解的概率趋近于1，称 算法在概率上是完整的。

位形空间障碍

位形空间C可以被划分为两部分，自由空间和障碍空间。关节限位可以被当作位形空间中的障碍物处理。

其他内容可以看书中的图，内容挺简单的。

到障碍物的距离与碰撞检测

可以用不同分辨率的球体来模拟机器人和障碍物，所以机器人和障碍物之间的距离为：机器人和障碍物上最近的球体的球心的距离减去两个球体的半径。

A*算法

A*算法主要是启发式函数h和代价函数g相加得到的f值来判断节点的分数，并优先扩展f分数低的节点周围的点，并同时更新代价函数g。
实现：
python版： 利用Python实现A*算法路径规划 - 静水流深的文章 - 知乎
这个内容写的非常的好，内容直观，并且有对应的可视化代码。
C++版本：
推荐一个博主的实现，曾经在工程中用过，感觉非常好。
https://github.com/zhangpanyi/a-star-algorithm 具体来说，做了几点优化： 1.建立一个和地图一样大的二维数组，通过查询的方法快速确定节点是否在openlist和closelist中。 2.构建二叉堆，通过上滤的方式实现sort操作,快速查找f值最小的节点。 3.将1进一步优化，将二维数组更新成一维数组。 4.新增节点的时候会调用C++的new函数频繁分配内存，在这里作者摘选了box2d（一个模拟2D刚体物体的 C++物理引擎）的小对象分配器来代替C++的new函数，又将速度提升了3倍。 最终效果：1000*1000的地图中以几毫秒的速度实现路径的搜索，十分高效和快速，建议大家去学习一下。

关于A*算法的内容，有几个需要掌握：

1. 启发式函数如果估计为0，则算法退化为迪杰斯特拉算法。而如果每条边成本都相同，则迪杰斯特拉算法退化为广度优先搜索算法。

2. 启发函数的估计值如果小于到终点的真实值，则一定能找到最优解。

3. 对启发式函数乘以大于1的常数因子，对启发函数进行过高估计，A*算法则慢慢偏向于贪心算法，找到解可能更快。但是这种方法不能保证找到最优解。

4. 允许斜着走，则使用欧几里德距离。不允许斜着走，则使用曼哈顿距离。东南西北邻居成本为1，对角邻居成本是根号二。工程上可以使用近似成本5和7来用整数计算代替。

5. A*算法路径规划器是分辨率完备的。

波前规划器（wavefront）

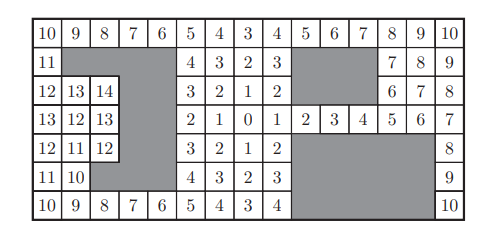
一言以蔽之：目标位形分数为0，用广度优先，从0开始向外扩散，扩散完地图后，从当前位置出发，按数字下坡即可。

有运动约束时的网格方法

轮式移动机器人

这个书中讲的很复杂，但其实就是考虑到了机器人的动力学约束，然后使用一个控制时间Δt，对离散的控制集合（线速度角速度）在Δt内进行积分，并且根据结果判断是否碰撞，并对应的扩展网格。

要求：

1. Δt要小，让运动步长变小

2. 网格尽可能大，节省计算

3. 确保离散控制集合中的任何控制在Δt时间内，能从一个网格移动到另一个网格。

机械臂网格规划

简单总结：

根据有限关节力矩情况下可行的加速度集合，确定离散的动作集合。

根据动作集合中的动作，用Δt进行积分，确定机械臂关节位置。并通过位置判断是否发生碰撞。广度优先搜索完，确定各个时刻的加速度动作。

为分辨率提升倍数， 为时间节省的倍数， 为关节数：
完成搜索的计算时间会扩充 倍。

RRT算法（快速探索随机树）

步骤可以简单概括：地图上随机采样点，然后找树中最近的点，然后从最近的点到随机点的方向延伸一段距离，未碰撞则加入树中。直到到达终点附近。

（当然也有算法随机采样点，是有0.5的概率随机采样，有0.5的概率直接选取终点）

1.RDT（快速探索密集树，Rapidly-exploring Dense Tree）， 不是采用随机采样的方法，而是采用确定性采样的方案， 在多分辨率的网格上逐渐密集采样。这个变种方法叫RDT。
2.RRT在“确定最近点“上可能没有那么简单，因为以汽车为例，侧方的看似离得近，因为它不能横着走，所以其实反而是不近的。
3.双向RRT：从起点和终点倒着走，交替生长，并且尝试连接两个树。（速度更快，但是缺点是可能找不到连接两个树的点）
4.RRT*：不断对节点进行重新连接，（判断各个点是否能以较低的代价到达新扩展的点）。RRT和RRT*在概率上是完备的，但RRT*找到的解更接近于最优解。

PRM算法（概率路线图Probabilistic RoadMap）

先采样N个点，然后找到每个点的k个最近的邻居，确定无碰撞的连接关系并进行连线。

在障碍物附近更密集的采样，可以提高通过狭窄通道的可能性。

虚拟势场法

• 目标提供吸引力，障碍物提供斥力。并且限制最大力，避免在障碍物附近产生无限大的力。

• 缺点是机器人可能会被卡在势场的局部最小值。

• 在得到合力以后，如何控制机器人？1.应用算出的力加阻尼，减少振荡。2.把力算作速度指令，消除振荡。

• 使用导航函数（navigation function）替换虚拟势函数。（即需要满足几点：1.在位置上两次可微，2.障碍物边界有最大值，3.目标点有最小值，4.在所有满足导航函数对位置求导为0的地方，二阶导数的海塞Hessian矩阵满秩），如果这样可以使得没有局部最小值。

• 对于受约束的机器人，可以把得到的合力，根据动力学那节的内容【现代机器人学】学习笔记七：开链动力学（前向动力学Forward dynamics 与逆动力学Inverse dynamics），用P矩阵，把用于约束的力滤掉，剩下的力用于控制。

非线性优化

和slam中的许多问题一样，非线性优化也是一个很好的方法。

在得到一个初值的情况下启动流程，并且参数化轨迹、或参数化控制，或二者都参数化（并且提供轨迹和控制之间的约束），进行非线性优化，通过优化的方式，得到最终的结果参数。

平滑

1. 对于非线性优化问题，添加一个成本代价函数，惩罚迅速变化的控制，从而使得控制平滑。这个思路还是蛮常见的，在我之前涉及到的强化学习控制机器人上也是一个经典的思路，其实并不限于优化问题。

2. 尝试连接较远的无碰撞点，这样近的波折点就可以被替换为一个长长的直线，避免之字形折返。