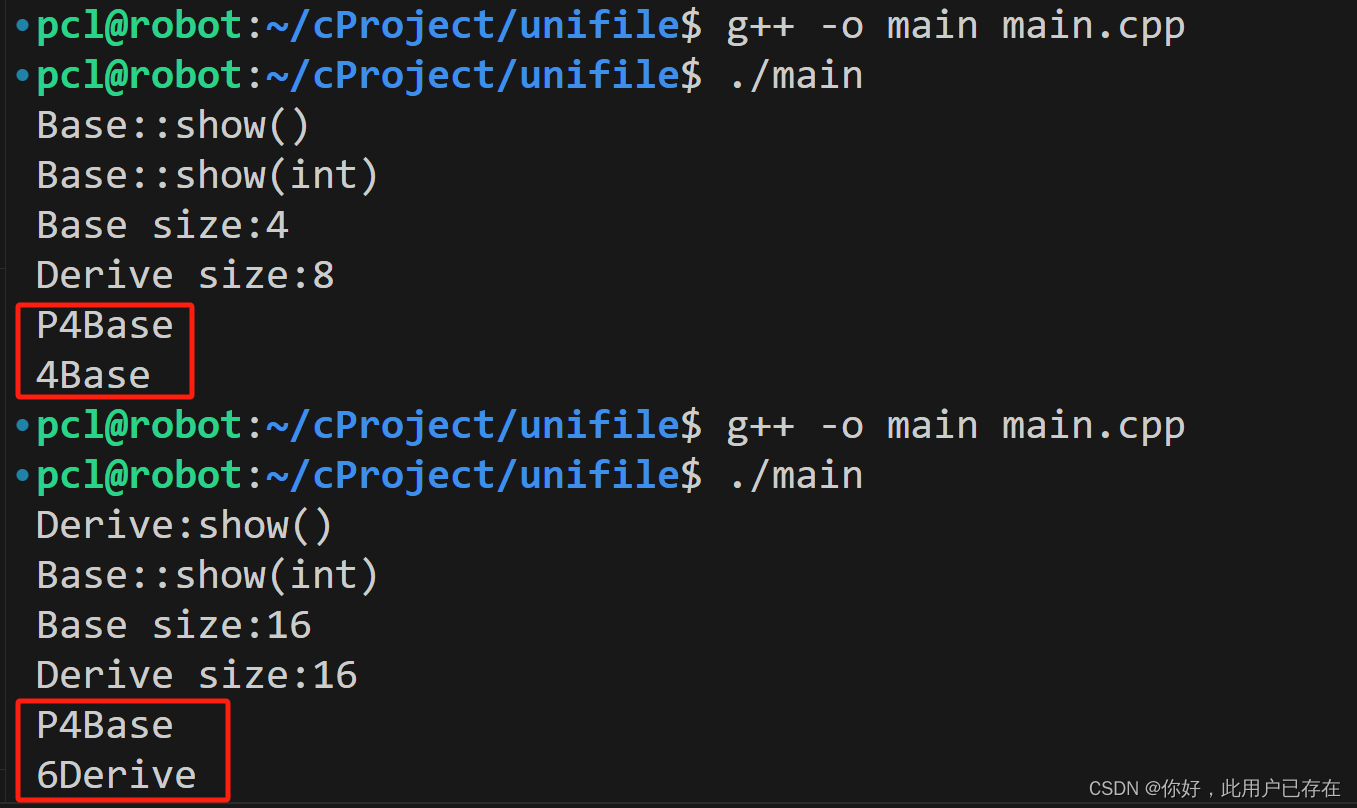
一、离散系统定义
离散系统是指系统的输入与输出仅在离散的时间上取值,而且离散的时间具有相同的时间间隔。满足下列条件:
①系统(的输入输出)每隔固定时间间隔才更新一次。固定时间间隔称为采样时间。
②系统的输出依赖当前的输入、以往的输入和输出。见数学描述
③系统具有离散的状态。状态是指系统前一时刻的输出量。
设系统的输入变量为其中n为采样时刻,Ts为系统的采样时间。由于Ts为固定值,因而系统输入
常被记为u(n)。设系统输出为y(nTs),也可记为y(n),则离散系统的数学描述为:
注:离散系统初始状态的确定非常重要。
二、离散Simulinlk仿真
有一个人口变化系统。设某一年的人口数目为p(n),其中n表示年份,它与上一年的人口数目p(n-1)、人口繁殖速率r以及新增资源所能满足的个体数目K之间的动力学模型如下差分方程:
此差分方程可看出系统为非线性离散系统。设人口初始值p(0)=600000,人口繁殖速率r为1.08,新增资源满足个体数K=200000,建立Simulink模型,分析人口数目的变化趋势。
(1)建立系统模型
Unit Delay为单位延迟模块,主要功能是将输入信号延迟一个采样时间,这里将p(n)作为它的输入以得到p(n-1)。
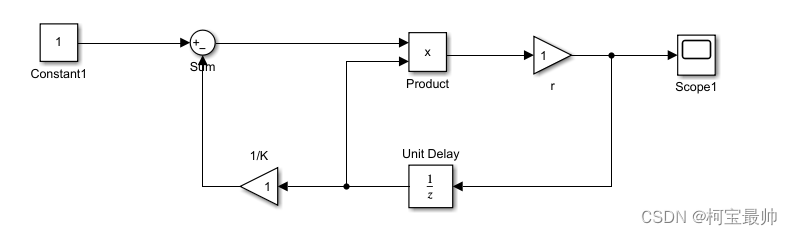
(2)模块参数设置
人口繁殖速率r:取1.08,
1/K:取1/2000000,
Unit Delay的初始值为初始人口数目:取600000。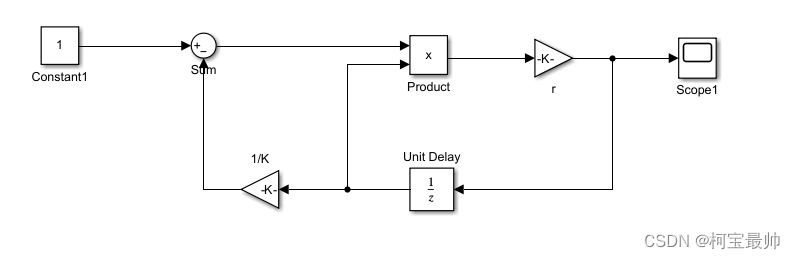
(3)仿真参数设置
仿真时间0~50s,求解器设置为discrete离散,即需要使用离散求解器;仿真步长选择Fixed-step定步长。
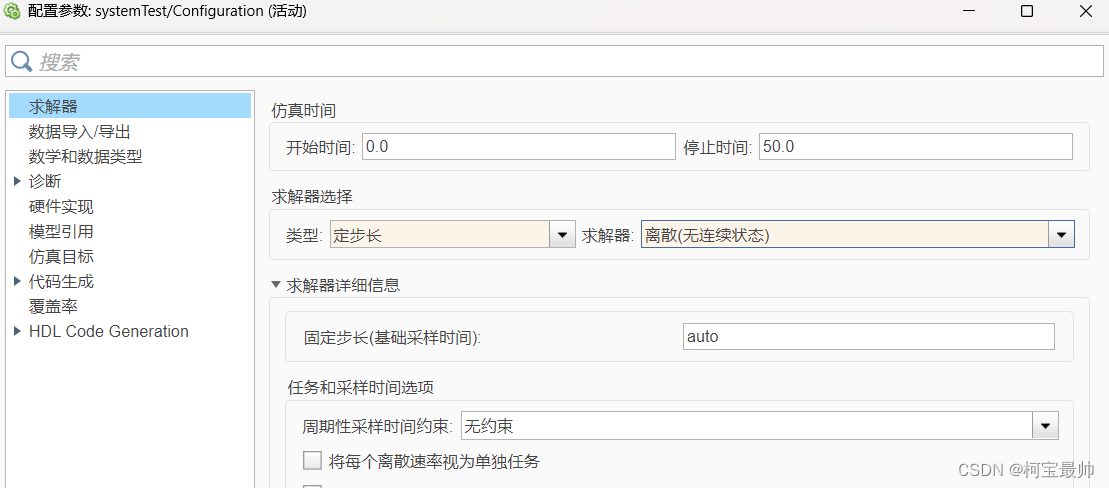
(4)仿真运行

注:若离散系统中所有模块的采样时间均相同,则此系统为单速率离散系统(选定步长求解器),否则为多速率离散系统(选变步长仿真更好)。
三、线性离散系统定义
在离散系统中,线性离散系统具有重要的地位。当离散系统同时满足齐次性和叠加性时,即:
此离散系统称为线性离散系统。最一般的数学描述为:
也可用差分方程描述(上为状态方程,下为输出方程):
除了上述两种方式,针对线性离散系统本身的特点,常使用Z变换来描述线性离散系统。Z变换时对离散信号进行分析的一个强有力工具,尤其线性离散系统。
对于一个离散信号u(n),其Z变换为,一般离散系统的时间大于0,则Z变换为
,简记为
。
利用离散信号的Z变换结果得到原离散信号的过程,叫做Z变换的逆变换,简记为。
Z变换有两个重要性质:
①Z变换同时满足齐次性和叠加性。
②若u(n)的Z变换为U(z),则u(n-1)的Z变换为。
四、线性离散系统Simulink仿真
低通滤波器模型。它可以滤除信号中的高频部分,以获取信号中有用的低频信号,一个低通数字滤波器的差分方程如下:
其中u(n)为滤波器输入,y(n)为滤波器输出。可见其为线性离散系统。
(1)Z变换
对该滤波器系统的差分方程进行Z变换,可得下面描述:
(2)建立系统模型
发送方首先使用高频正弦波(载波)对一低频锯齿波(原信号波)进行幅度调制,然后在无损信道中传递此幅度调制信号;接受方在接收到幅度调制信号后,首先进行解调,然后使用低通数字滤波器对解调后的信号进行滤波以获得低频锯齿波信号。

Sine Wave用来产生高频载波信号,Sine Wave1用来产生解调信号;
Signal Generator产生低频锯齿波信号;
Discrete Filter表示数字滤波器。
(3)模块参数设置
高频载波(Sine Wave)频率设置为1000rad/sec,其余默认;Signal Generator波形选择锯齿波sawtooth,其余默认;解调正弦波(Sine Wave1)频率也为1000rad/sec,采样时间0.005s。
Discrete Filter设置如下:
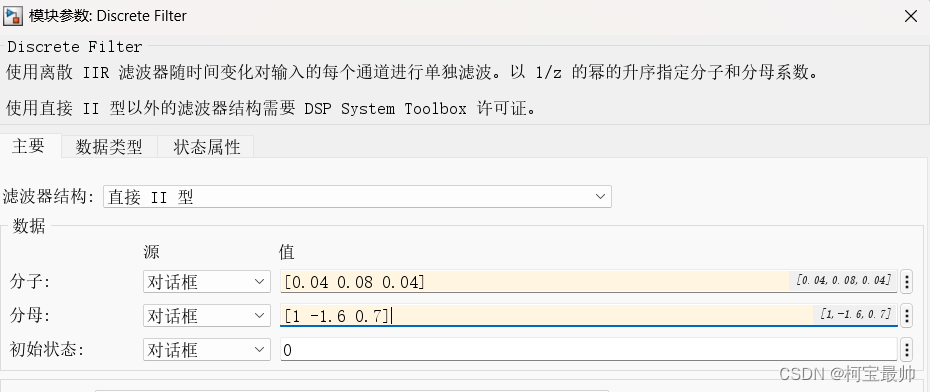
注:数字滤波器的采样时间应该与解调信号的采样时间一致。
(4)仿真参数设置
仿真时间0~10s,选择求解器并设置为Variable-step变步长、ode45(Dormand-Prince),最大步长设置为0.005。
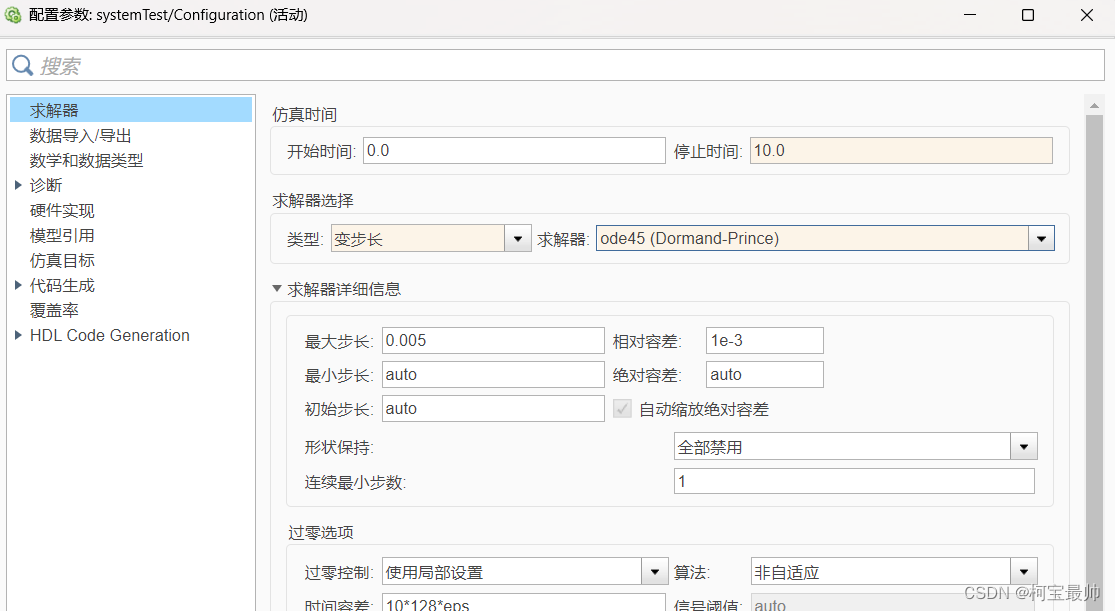
(5)仿真运行
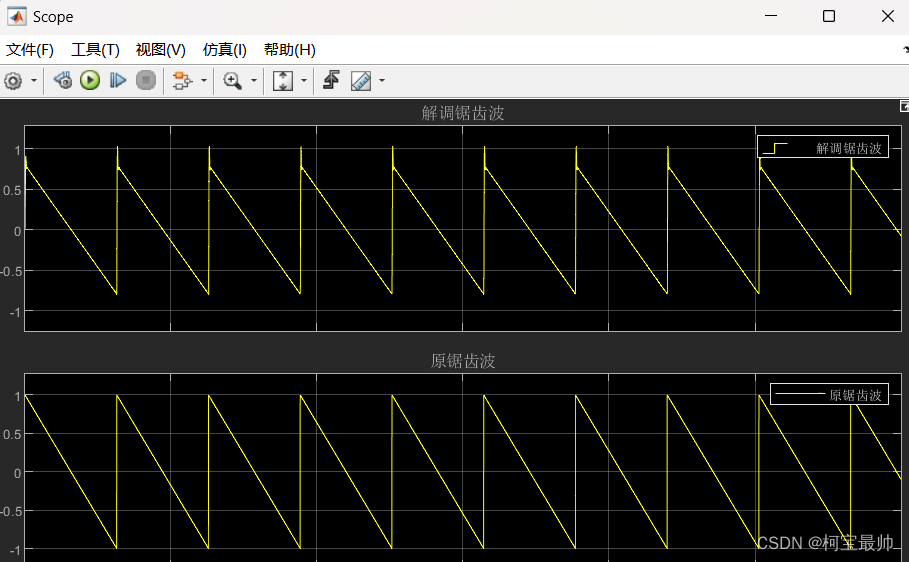
数字滤波器的输出信号与原始锯齿信号并不完全一致,存在一定失真,这种失真不可避免,因为实际上并不存在理想的滤波器,调制时信号之间不可避免会相互干扰。
疑问:博友们,这里遇到各问题,锯齿波的scope显示周期与设定的信号周期不一致???
往期精彩
STM32专栏(付费9.9)![]() http://t.csdnimg.cn/E2F88
http://t.csdnimg.cn/E2F88
OpenCV-Python专栏(付费9.9)![]() http://t.csdnimg.cn/zK1jV
http://t.csdnimg.cn/zK1jV
AI底层逻辑专栏(付费9.9)![]() http://t.csdnimg.cn/zic0f
http://t.csdnimg.cn/zic0f
机器学习专栏(免费)![]() http://t.csdnimg.cn/FaXzAFreeRTOS专栏(免费)
http://t.csdnimg.cn/FaXzAFreeRTOS专栏(免费)![]() http://t.csdnimg.cn/SjIqU电机控制专栏(免费)
http://t.csdnimg.cn/SjIqU电机控制专栏(免费)![]() http://t.csdnimg.cn/FNWM7
http://t.csdnimg.cn/FNWM7












![【蓝桥杯冲冲冲】[NOIP2001 普及组] 装箱问题](https://img-blog.csdnimg.cn/direct/6e67173901fe4580b2975a4c0c11abb1.jpeg#pic_center)