思路：

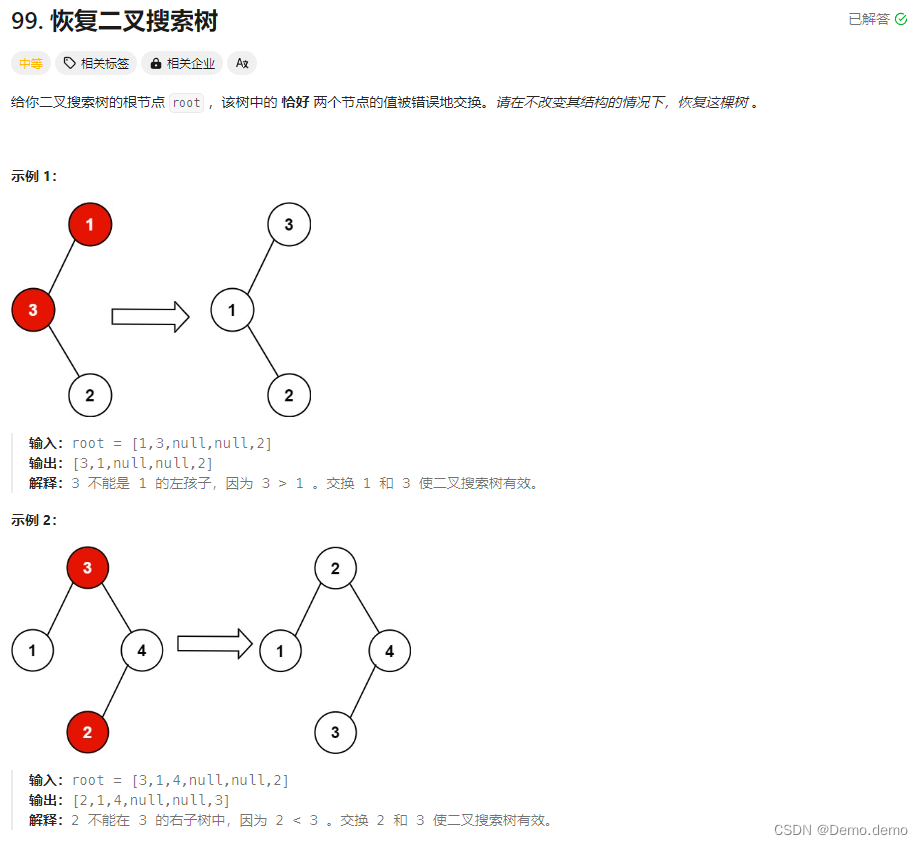
二叉搜索树的中序遍历是递增序列，可以在中序遍历中记录两个需要交换的节点，直到遍历完毕之后，对两个节点的值进行交换即可得到正确的二叉搜索树

比如中序序列为  1  2   3  7  5  6  4（7比5大记录7为x，6比4大记录4为y，交换x与y）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //用于记录交换节点以及前一个节点
    TreeNode* x = nullptr;
    TreeNode* y = nullptr;
    TreeNode* pre = nullptr;
    void recoverTree(TreeNode* root) {
        //进行中序遍历
        dfs(root);
        //如果交换节点都不为空，则进行val交换得到结果
        if(x!=nullptr&&y!=nullptr){
            int temp = x->val;
            x->val = y ->val;
            y->val = temp;
        }
    }
    //中序遍历
    void dfs(TreeNode* root) {
        //如果为空节点，返回
        if(root == nullptr) return;
        //遍历左子树
        dfs(root->left);
        //如果当前节点为第一个节点，则pre = 当前节点
        if(pre == nullptr) pre = root;
        //如果当前节点前面有节点
        else{
            //如果当前节点的值小于前一个节点的值
            if(pre->val > root->val){
                //记录当前节点的值，不停的更新y的节点
                y = root;
                //如果另一个节点为空，则记录前一个节点，固定x节点
                if(x == nullptr) x = pre;
            }
            //每次遍历都需要更新pre节点，即当前节点为前一个节点
            pre = root;
        }
        //遍历右子树
        dfs(root->right);
    }
};