题目1：62 不同路径

题目链接：62 不同路径

题意

机器人位于m*n网格的左上角每次只能向下或向右移动一步，到达网格的右下角,返回不同路径的数量

动态规划

动规五部曲

1）dp数组及下标i的含义

dp[i][j]：到达(i,j)有dp[i][j]条路径

2）递推公式

dp[i][j] = dp[i-1][j] + dp[i][j-1]

3）dp数组初始化（注意）

根据递推公式 最上面一行要初始化  dp[0][j] = 1     最左面一列要初始化  dp[i][0] = 1

4）遍历顺序

由于dp[i][j]与dp[i-1][j]和dp[i][j-1]有关，从上到下遍历，从左往右遍历

5）打印dp数组

代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m,vector<int>(n));
        //初始化
        for(int i=0;i<m;i++) dp[i][0] = 1;
        for(int j=0;j<n;j++) dp[0][j] = 1;
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

• 时间复杂度：O(m × n)
• 空间复杂度：O(m × n)

题目2：63 不同路径Ⅱ

题目链接：63 不同路径Ⅱ

题意

机器人位于m*n网格的左上角，每次只能向下或向右移动一步，最终到达右下角，网格中有障碍物，障碍物和空格用1和0表示，不同的路径数量

动态规划

动规五部曲

1）dp数组及下标i的含义

dp[i][j]：到达(i,j)有dp[i][j]条路径

2）递推公式

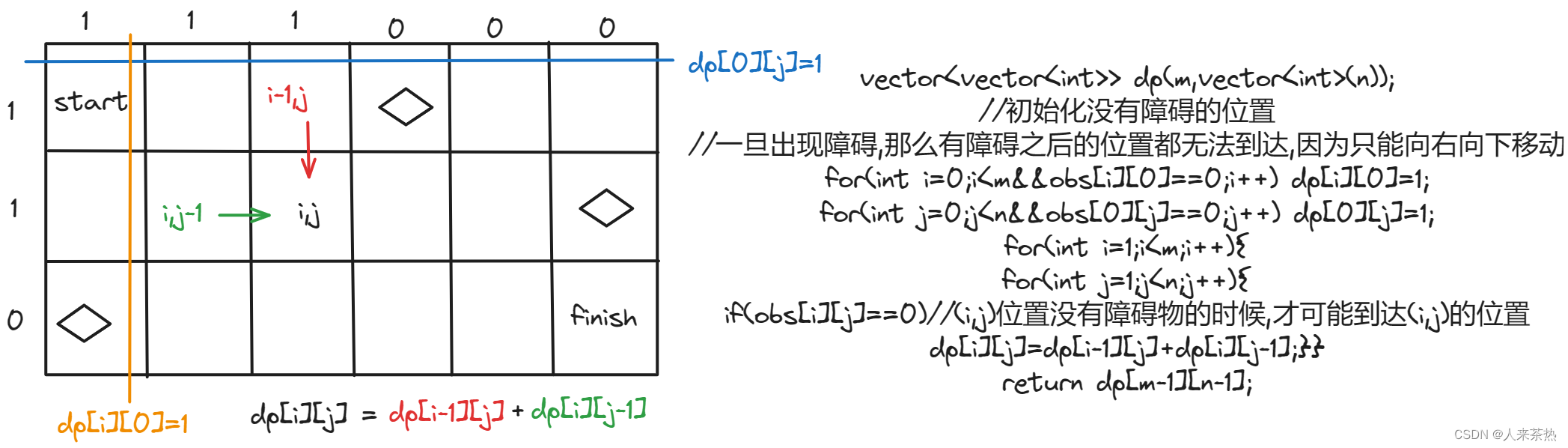
位置没有障碍才推到   if(obs[i][j]==0)   dp[i][j] = dp[i-1][j] + dp[i][j-1]

3）dp数组初始化（注意）

根据递推公式

最上面一行要初始化  if(obs[0][j]==0) dp[0][j] = 1     出现障碍物以及障碍物之后的位置达不到，因为一直向右或向下移动

最左面一列要初始化  if(obs[i][0]==0) dp[i][0] = 1     出现障碍物以及障碍物之后的位置达不到，因为一直向右或向下移动

起始位置有障碍或终止位置有障碍，有0种路径

4）遍历顺序

由于dp[i][j]与dp[i-1][j]和dp[i][j-1]有关，从上到下遍历，从左往右遍历

5）打印dp数组

代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        if(obstacleGrid[0][0]==1) return 0;
        if(obstacleGrid[m-1][n-1]==1) return 0;
        //定义dp数组
        vector<vector<int>> dp(m,vector<int>(n));
        //初始化dp数组
        for(int i=0;i<m && obstacleGrid[i][0]==0;i++) dp[i][0] = 1;
        for(int j=0;j<n && obstacleGrid[0][j]==0;j++) dp[0][j] = 1;
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(obstacleGrid[i][j]==0){
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

• 时间复杂度：O(m × n)
• 空间复杂度：O(m × n)