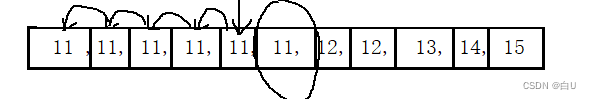一、概念

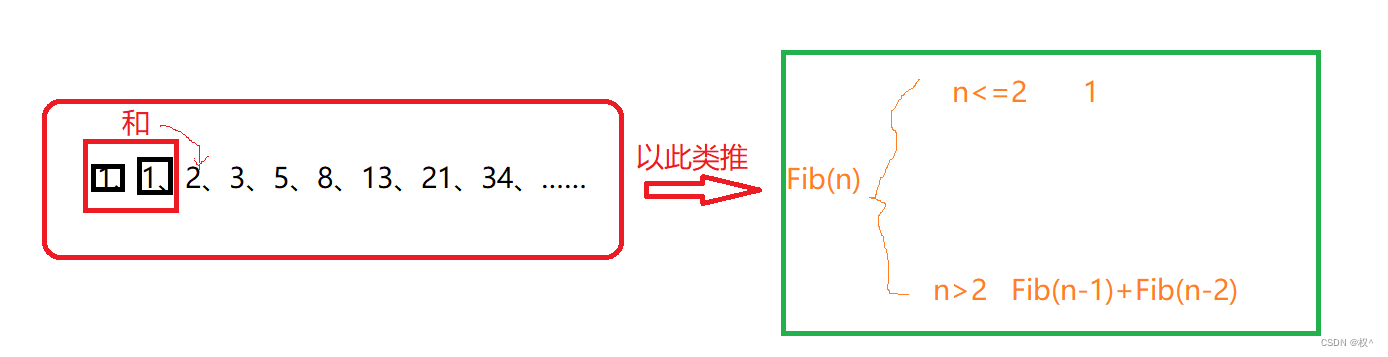
斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1）+F(n - 2)（n ≥ 2，n ∈ N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

二、用迭代求第n个斐波那契数

1.分析

2.完整代码

#include<stdio.h>
int Fib(int n)
{
	if (n<=2)
	{
		return 1;
	}
	else
	{
		return Fib(n - 1)+Fib(n - 2);
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret=Fib(n);
	printf("%d", ret);
	return 0;
}

3.运行结果

查数据得:
第五项斐波那契数是：5。

4.如果求第50个斐波那契数呢？看看会怎么样。

运行结果：

当我们n输⼊为50的时候，需要很⻓时间才能算出结果，这个计算所花费的时间，是我们很难接受的，这也说明递归的写法是非常低效的，那是为什么呢？
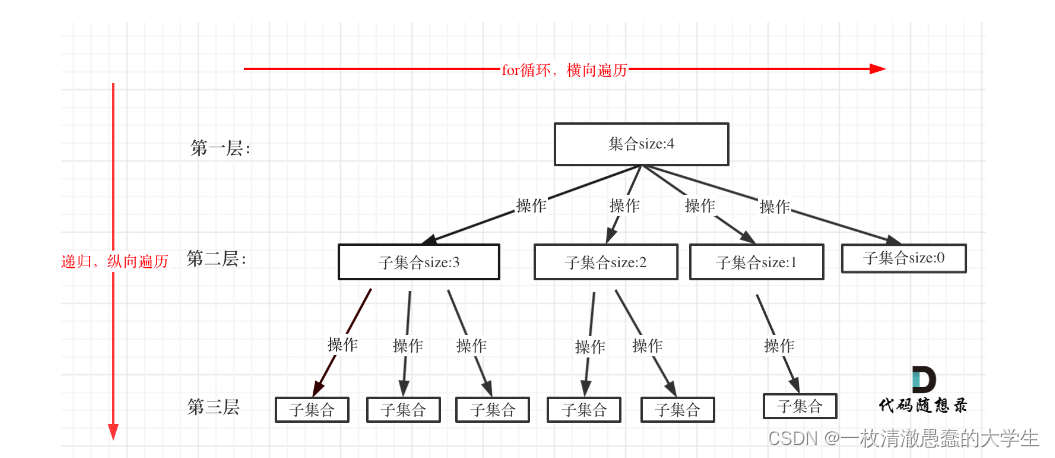
其实递归程序会不断的展开，在展开的过程中，我们很容易就能发现，在递归的过程中会有重复计算，而且递归层次越深，冗余计算就会越多。
进行测试：

#include <stdio.h>
int count = 0;
int Fib(int n)
{
 if(n == 3)
 count++;//统计第3个斐波那契数被计算的次数
 if(n<=2)
 return 1;
 else
 return Fib(n-1)+Fib(n-2);
}
int main()
{
 int n = 0;
 scanf("%d", &n);
 int ret = Fib(n);
 printf("%d\n", ret); 
 printf("\ncount = %d\n", count);
 return 0;
}

4.1运行结果：

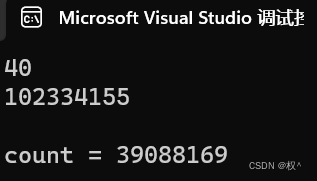
这里我们看到了，在计算第40个斐波那契数的时候，使用递归方式，第3个斐波那契数就被重复计算了39088169次，这些计算是非常冗余的。所以斐波那契数的计算，使用递归是非常不明智的，我们就得想迭代的方式解决。

4.2画图解释

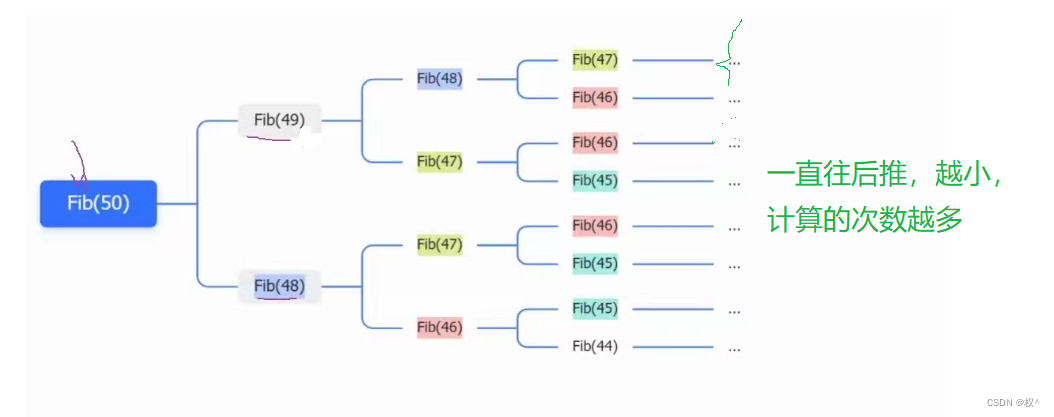
三、用迭代的方式求第n个斐波那契数列

1.分析

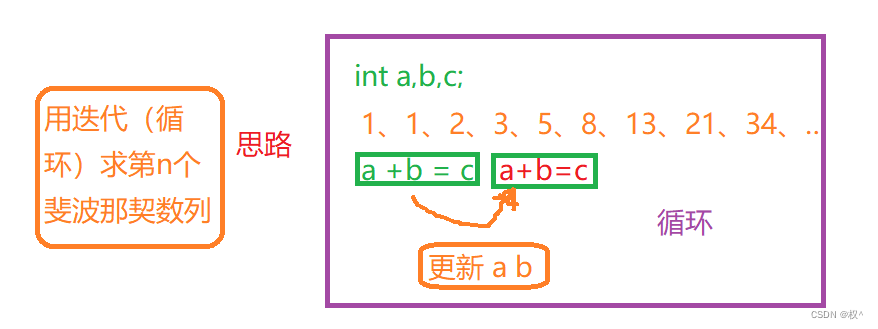
2.完整代码

#include<stdio.h>
int Fib(int n)
{
int a = 1, b = 1, c = 1;
	while (n > 2)
	{
		a = b;
		b = c;
		c = a + b;
		n--;
	}
	return c;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int numb = Fib(n);
	printf("%d", numb);
}

3.运行结果

4.求第50个斐波那契数

4.1运行结果

这个结果的出现花费的时间非常快，

4.2运行结果的解释

这个第50个斐波那契数太大了，一个整型放不下，所以是负滴。

四、总结

青蛙跳台阶问题，也是属于求n个斐波那契数列。有时候，递归虽好，但是也会引⼊⼀些问题，所以我们⼀定不要迷恋递归，恰到好处就好。

欧耶！！！！我学会啦！！！！！！