题目链接:https://leetcode.cn/problems/regular-expression-matching/
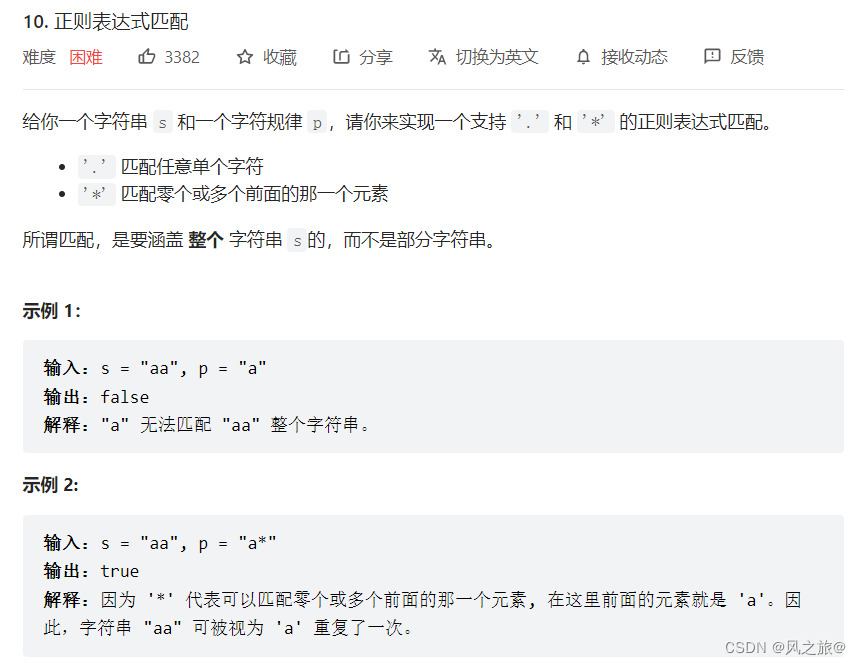
从暴力递归到动态规划,对于状态转移方程不容易推导出来的可以先从递归进行尝试各种策略,最后再从暴力递归转为动态规划,这种尝试方式容易求解dp初始值以及dp更新方式,由于题目限制了s的长度最大为20,p的长度最大为30,这道题使用暴力递归的解法也过了。暴力递归和动态规划的具体解题思路如下:
暴力递归:题目是两个字母串匹配的过程,可以使用递归分解成子问题来做
递归方程的定义:boolean process(char[] s, char[] p, int sL, int pL),参数解释如下:
s:字符串s
p:字符规律p
sL:从字符串s的sL处位置开始匹配
pL:从字符规律p的pL处位置开始匹配
return:如果p[pL,...,N]完全匹配字符串s[sl,...,M]则,返回true,否则返回false
process递归函数的解释:判断字符规律p从索引pL开始一直到结束的正则表达式字符串是否匹配字符串s从索引sL开始到结束的字符串
递归的结束条件:对于递归函数来说首先需要找到递归的结束条件
如果sL==s.length:这种情况字符串s已经完全被正则表达式匹配了(s最后一个字符的索引为s.length-1),但是字符规律p可能还没有结束,需要分情况讨论:
pL == p.length:正则表达式也结束了(正则表达式的最后一个字符的索引为p.length-1),显然这种情况正则表达式p完全匹配字符串s,递归函数返回true
否则:正则表达式还没有使用完,但是这种情况并不意味着正则表达式没有全部匹配字符串s,因为有*(匹配零个或多个前面的哪一个元素,这种情况会把没有使用完的正则字符消耗掉),
比如字符串s="a",字符规律p="ab*",字符规律p的a匹配字符串s的a,字符串s匹配结束,但是字符规律p还剩下字符"b*",这个时候显然完全匹配的,递归函数应该返回true
比如字符串s="a",字符规律p="ab",字符规律p的a匹配字符串s的a,字符串s匹配结束,但是字符规律p还剩下字符"b",这个时候显然是不匹配的,递归函数应该返回false
因此,当字符串s结束,字符规律p还有字符时,需要再次判断,如果p剩余字符是*,让pL++,如果p[pL + 1] == '*',可以让*的含义为匹配零次,把*前面的一个字符消耗掉,让pL=pL+2,最终如果pL大于等于p.length,这个是否显然字符规律p也消耗完,递归函数返回true,否则返回false
如果,sL!=s.length,但是pL==p.length:这种情况为字符串s还有字符,但是正则表达式全部消耗完了,这种情况递归返回false
递归的终止条件已经找到,接下来就是递归的转移过程了,此时,字符串s和字符规律p都有剩余字符。需要分三种情况,对于字符归路p,只有三种字符,".","*",“a-z”
p[pL] == '.':字符规律当前的字符为"." ,可以匹配任意一个字符s中的字符,分两种情况
如果p[pL+1]=="*":表明当前.可以选择匹配零个或者匹配任意多个字符,最终递归转移有两种
p1 = process(s, p, sL, pL + 1):当前的. 选择匹配0个s中的字符,p中的.被消耗掉,然后看s[sL,...M]和p[pL+1,...,N]是否完全匹配
p2 = process(s, p, sL + 1, pL + 1):当前的. 选择匹配多个(>=1)个s中的字符,p中的.和s的当前字符消耗掉,然后看s[sL+1,...,M]和p[pL+1,...N]是否完全匹配,解释一下,这里为什么是pL+1而不是pL(把当前的.消耗掉了),下一个字符为*,当前的.不是可以匹配多次吗?因为下一个字符是*,匹配多次的逻辑在*中判断,这样可以减少递归的层数
只要a和b两个递归中有一个返回true,那么就表明存在一个正则匹配使字符规律p完全匹配字符串s,因此递归返回值为p1=p1||process(s, p, sL + 1, pL + 1)
否则,也就是.的下一个字符不是*,当前.只能匹配一个字符,递归返回值为:p1=process(s, p, sL + 1, pL + 1)
如果p[pL] == '*',那么p的前面一个字符可以匹配多次,分两种情况
确定使用哪一个字符去匹配:
如果p[pL - 1] == '.',那么,可以匹配掉任何一个s中的字符即c=s[sL](s中待消耗掉的字符),
否则,c=p[pL-1],只能使用p中前一个字符取匹配
递归转移:
匹配0个,p1 = process(s, p, sL, pL + 1):选择匹配0个,p中的*被消耗掉
c == s[sL]时,p2 = process(s, p, sL + 1, pL):选择匹配多个,s的当前字符被消耗掉,p中的*继续使用
c!==s[sL]时,p2 = process(s, p, sL, pL + 1):p的前一个字符和s当前的字符不匹配,只能选择匹配0个(这个分支在程序中不用写,因为在a中已经判断匹配0个了,这里列出为了逻辑清晰)
只要p1和p2有一个为true,那么说明存在一个正则匹配方式使字符规律p完全匹配字符串s,因此递归返回p1||p2
否则,也就是p的当前字符为字母:分两种情况
如果s[sL] == p[pL]:正确匹配,有两种情况:
如果p[pL + 1] == '*':p的下一个字符为*,当前p中的字符可以选择匹配0次或者多次
p1 = process(s, p, sL, pL + 1):匹配0次,也就是不用p中的字符消耗s中的当前字符,仅p中的当前字符被消耗掉
p2 = process(s, p, sL + 1, pL + 1):匹配多次,s中的当前字符和p的当前字符被消耗掉
p1 = p1 || process(s, p, sL + 1, pL + 1)
否则,只能匹配一次,p1 = process(s, p, sL + 1, pL + 1)
递归返回p1
如果s[sL] != p[pL]
如果p[pL + 1] == '*':虽然当前不匹配,但是p的下一个字符是*,可以将当前不匹配的字符消耗掉递归返回值为process(s, p, sL, pL + 1)
否则,就只能返回false了。
AC代码
class Solution {
public static boolean isMatch(String s, String p) {
return process(s.toCharArray(), p.toCharArray(), 0, 0);
}
public static boolean process(char[] s, char[] p, int sL, int pL) {
if (sL == s.length) {
if (pL == p.length) {
return true;
} else {
while (pL < p.length) {
if (p[pL] == '*') {
pL++;
} else {
if (pL + 1 < p.length && p[pL + 1] == '*') {
pL += 2;
} else {
break;
}
}
}
return pL >= p.length;
}
}
if (pL == p.length) {
return false;
}
if (p[pL] == '.') {
boolean p1;
if (pL + 1 < p.length && p[pL + 1] == '*') {
p1 = process(s, p, sL, pL + 1);
p1 = p1 || process(s, p, sL + 1, pL + 1);
} else {
p1 = process(s, p, sL + 1, pL + 1);
}
return p1;
} else if (p[pL] == '*') {
char c;
if (p[pL - 1] == '.') {
c = s[sL];
} else {
c = p[pL - 1];
}
boolean p1 = process(s, p, sL, pL + 1);
if (c == s[sL]) {
p1 = p1 || process(s, p, sL + 1, pL);
}
return p1;
} else {
if (s[sL] == p[pL]) {
boolean p1;
if (pL + 1 < p.length && p[pL + 1] == '*') {
p1 = process(s, p, sL, pL + 1);
p1 = p1 || process(s, p, sL + 1, pL + 1);
} else {
p1 = process(s, p, sL + 1, pL + 1);
}
return p1;
} else {
int p1;
if (pL + 1 < p.length && p[pL + 1] == '*') {
return process(s, p, sL, pL + 1);
}
return false;
}
}
}
}虽然过了,但是也是险过,时间花费太大....
动态规划:可以直接由上述递归求解修改成动态规划求解
dp数组的维度与大小:递归函数process(char[] s, char[] p, int sL, int pL)变化的的参数只有两个sL和pL,因此只需要两个维度,就可以表示所有的递归过程,又因为递归终止条件为sL == s.length或者pL==p.length,即从0到s.length,因此使用dp[s.length+1][p.length+1]就可以保存所有的递归函数,其中dp[sL][pL]=process(char[] s, char[] p, int sL, int pL)
dp数组的初始值:由递归方程的终止条件就是dp数组的初始值,其中dp[s.length][p.length] = true,字符串s和字符规律p都已经到达末尾,递归函数返回true
dp[s.length][p.length] = true;
for (int pL = 0; pL < p.length; pL++) {//sL == s.length
int j = pL;
while (j < p.length) {
if (p[j] == '*') {
j++;
} else {
if (j + 1 < p.length && p[j + 1] == '*') {
j += 2;
} else {
break;
}
}
}
dp[s.length][pL] = j >= p.length;
}
for (int sL = 0; sL < s.length; sL++) {//pL==p.length
dp[sL][p.length] = false;
}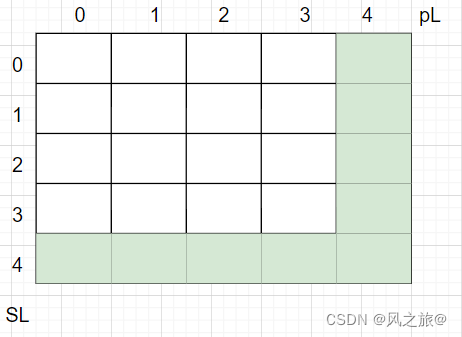
经过上述过程我们就可以求出上图中dp数组的最下面一行和最最边一行的初始值
dp的状态转移:对于递归process(char[] s, char[] p, int sL, int pL),在本次递归函数中会进入下面几层递归
process(s, p, sL, pL + 1)
process(s, p, sL + 1, pL + 1)
process(s, p, sL + 1, pL)
也就是dp[sL][pL]的值会和dp[sL][pL+1],dp[sL+1][pL+1],dp[sL+1][pL]相关
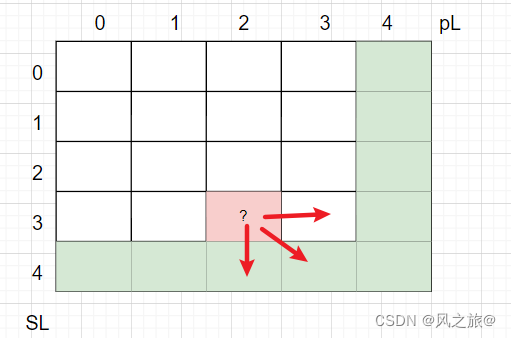
如果想要求出?处的值,需要直到右边,下边,右下角的值,而最下面一行和最右边一行的值已经求出,所以可以从下往上,从左往右更新dp数组,将所有的process(s,p,sL,pL)递归函数改为响应的dp数组,所有的return部分使用dp数组保存递归函数返回结果(这就是dp的状态转移!),暴力递归求解中,第一层递归为rocess(s.toCharArray(), p.toCharArray(), 0, 0),所以最终返回值为dp[0][0]
AC代码
class Solution {
public static boolean isMatch(String s, String p) {
return dp(s.toCharArray(), p.toCharArray());
}
public static boolean dp(char[] s, char[] p) {
boolean[][] dp = new boolean[s.length + 1][p.length + 1];
dp[s.length][p.length] = true;
for (int pL = 0; pL < p.length; pL++) {
int j = pL;
while (j < p.length) {
if (p[j] == '*') {
j++;
} else {
if (j + 1 < p.length && p[j + 1] == '*') {
j += 2;
} else {
break;
}
}
}
dp[s.length][pL] = j >= p.length;
}
for (int sL = 0; sL < s.length; sL++) {
dp[sL][p.length] = false;
}
for (int sL = s.length - 1; sL >= 0; sL--) {
for (int pL = p.length - 1; pL >= 0; pL--) {
if (p[pL] == '.') {
boolean p1;
if (pL + 1 < p.length && p[pL + 1] == '*') {
p1 = dp[sL][pL + 1];
p1 = p1 || dp[sL + 1][pL + 1];
} else {
p1 = dp[sL + 1][pL + 1];
}
dp[sL][pL] = p1;
} else if (p[pL] == '*') {
char c;
if (p[pL - 1] == '.') {
c = s[sL];
} else {
c = p[pL - 1];
}
boolean p1 = dp[sL][pL + 1];
if (c == s[sL]) {
p1 = p1 || dp[sL + 1][pL];
}
dp[sL][pL] = p1;
} else {
if (s[sL] == p[pL]) {
boolean p1;
if (pL + 1 < p.length && p[pL + 1] == '*') {
p1 = dp[sL][pL + 1];
p1 = p1 || dp[sL + 1][pL + 1];
} else {
p1 = dp[sL + 1][pL + 1];
}
dp[sL][pL] = p1;
} else {
if (pL + 1 < p.length && p[pL + 1] == '*') {
dp[sL][pL] = dp[sL][pL + 1];
} else {
dp[sL][pL] = false;
}
}
}
}
}
return dp[0][0];
}
}
时间从暴力递归的1091ms缩短为1ms!
从暴力递归到动态规划完全没有推导出dp的状态转移方程,只是从暴力递归进行尝试,然后根据递归修改为动态规划,这种方式比较简单,对于直接推到状态转移方程比较困难的情况,不妨先从暴力递归进行尝试,然后修改成动态规划。