洛谷P1002 过河卒（简单DP）

news2024/9/27 19:23:42

[NOIP2002 普及组] 过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示， $A$ 点 $(0, 0)$ 、 $B$ 点 $(n, m)$ ，同样马的位置坐标是需要给出的。

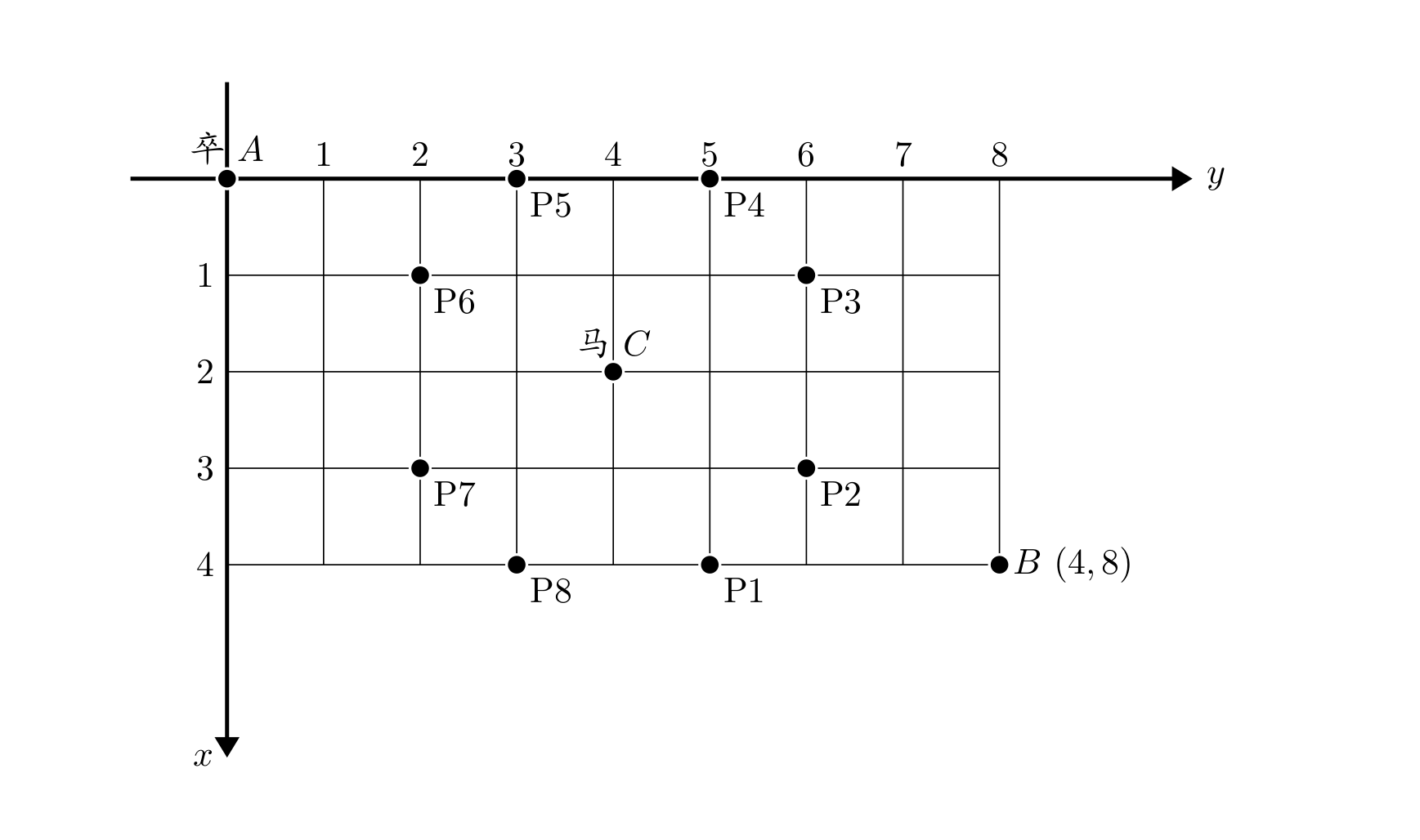
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

提示

对于 $\%$ 的数据， $\le n, m \le 20$ ， $\le$ 马的坐标 $\le 20$ 。

此题和摘花生类似，都是路线问题，并且思考方法也是一样的，就是中间加了个马需要特别注意一下（马的位置还有它八个可能到的点）。
状态表示： f[i][j] 表示终点为（i，j）的所有路线
状态计算： f[i][j] = f[i - 1][j] + f[i][j - 1],表示分别是从上面和左面到达（i，j）点的，两种情况应该求和。更新的条件是不在那九个点上，如果在点上则直接跳过。

完整代码（注解版）

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cmath>
using namespace std;

const int N = 25;
int n, m, x, y;
long long f[N][N];
bool ma[N][N];
int num[8][2] = {{1, 2}, {1, -2}, {2, 1}, {2, -1}, {-1, 2}, {-1, -2}, {-2, 1}, {-2, -1}};

int main () {
	cin >> n >> m >> x >> y;
	// 因为马的可能点涉及到-2，所以将四个数先+2，防止数组越界
	x += 2;
	y += 2;
	n += 2;
	m += 2;
	// 标记马的位置
	ma[x][y] = true;
	// 初始化，当我们计算第一个数时，f[2][2] = f[1][2] + f[2][1]，它应该为1（我们没有给
	// 坐标加2时，它是f[0][0],从（0,0）到（0,0）肯定只有1条路线）
	// 所以必须得将f[1][2]或f[2][1]初始化为1，否则所有数计算出来都是0
	f[2][1] = 1;
	// 把有马的地方标记
	for (int i = 0; i < 8; i ++) {
		ma[ x + num[i][0]][y + num[i][1]] = true;
	}

	for (int i = 2; i <= n; i ++) {
		for (int j = 2; j <= m; j ++) {
			if (ma[i][j])
				continue;
			f[i][j] = f[i - 1][j] + f[i][j - 1];
		}
	}
	cout << f[n][m] << endl;
	return 0;
}