文章目录
- [A - DFS搜索](https://ac.nowcoder.com/acm/contest/67741/A)
- [B - 关鸡](https://ac.nowcoder.com/acm/contest/67741/B)
- [C - 按闹分配](https://ac.nowcoder.com/acm/contest/67741/C)
- [D - 数组成鸡](https://ac.nowcoder.com/acm/contest/67741/D)
- [E - 本题又主要考察了贪心](https://ac.nowcoder.com/acm/contest/67741/E)
- [F - 鸡数题!](https://ac.nowcoder.com/acm/contest/67741/F)
- [G - why买外卖](https://ac.nowcoder.com/acm/contest/67741/G)
- [H - 01背包,但是bit](https://ac.nowcoder.com/acm/contest/67741/H)
- [I - It's bertrand paradox. Again!](https://ac.nowcoder.com/acm/contest/67741/I)
- [L - 要有光](https://ac.nowcoder.com/acm/contest/67741/L)
- [M - 牛客老粉才知道的秘密](https://ac.nowcoder.com/acm/contest/67741/M)
A - DFS搜索
字符串匹配
int n;
string DD = "DFS", dd = "dfs";
void solve() {
int D = 0, d = 0;
string s; cin >> n >> s;
for (int i = 0; i < n; i ++)
if (s[i] == DD[D]) D ++;
else if (s[i] == dd[d]) d ++;
cout << (D >= 3) << ' ' << (d >= 3) << endl;
}
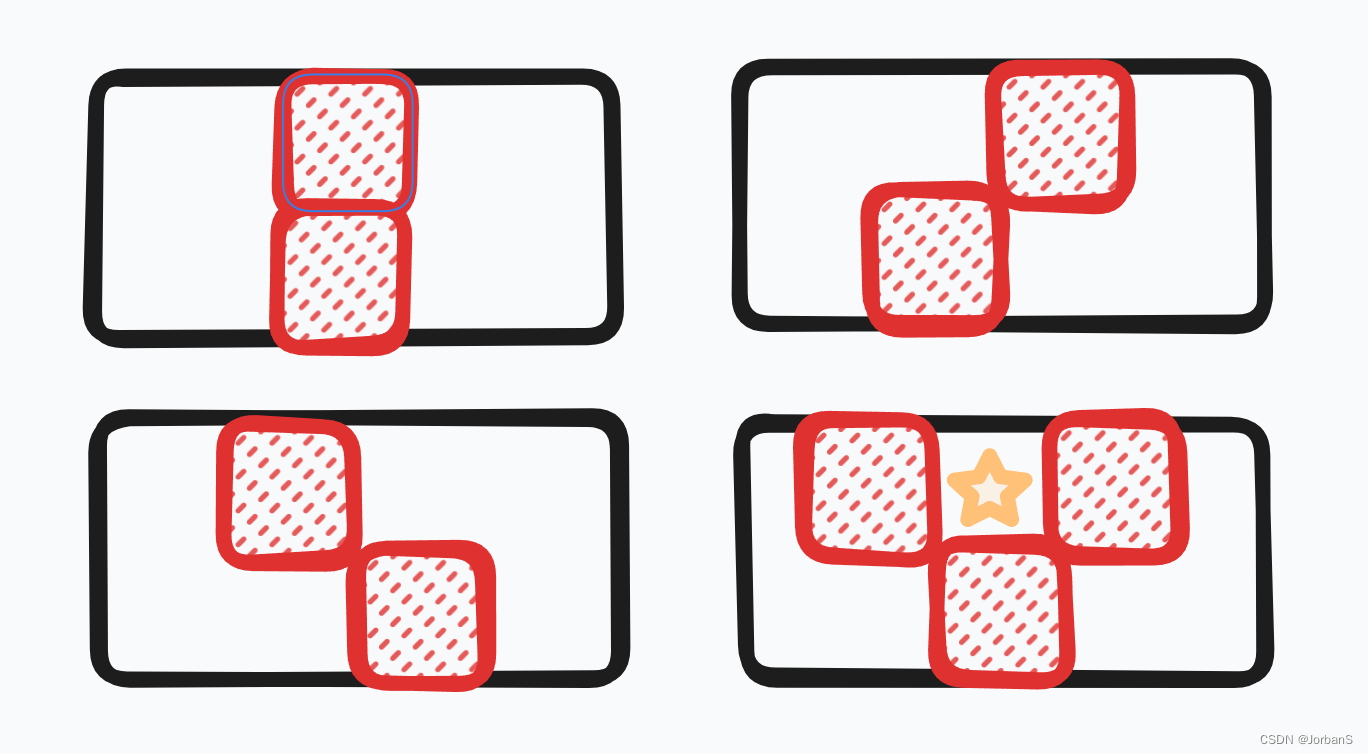
B - 关鸡
有以下四种基本图形,排列组合即可
int n;
pii a[N];
int solve() {
cin >> n;
for (int i = 0; i < n; i ++) cin >> a[i].bb >> a[i].aa;
sort(a, a + n);
int res = 3;
bool down = false, L = false, R = false, left = false, right = false;
bool ll = false, rr = false;
for (int i = 0; i < n; i ++) {
if (a[i].aa == 0 && a[i].bb == 2) down = true;
if (a[i].aa == -1 && a[i].bb == 1) left = true;
if (a[i].aa == 1 && a[i].bb == 1) right = true;
if (a[i].aa < 0) ll = true;
if (a[i].aa > 0) rr = true;
if (i) {
if (a[i].aa == a[i - 1].aa) {
if (a[i].aa < 0) L = true;
else R = true;
} else if (a[i].aa - 1 == a[i - 1].aa && a[i].bb + a[i - 1].bb == 3) {
if (a[i - 1].aa < 0) L = true;
else if (a[i].aa > 0) R = true;
}
}
}
if (L && R || down && left && right) return 0;
if (L && right && down || R && left && down) return 0;
if (down && left || down && right || left && right) return 1;
if (L && right || R && left || L && down || R && down) return 1;
if (L && rr || R && ll) return 1;
if (left && down && rr || right && down && ll) return 1;
if (L || R || down || left || right || ll && rr) return 2;
return 3;
}
C - 按闹分配
排序后,前缀和人等待的时间,二分查找鸡插队的时间点
int n, m;
ll t, q;
ll a[N];
bool check(ll x) {
int l = upper_bound(a + 1, a + n + 1, x) - a;
ll res = (n - l + 1) * t;
return res <= q;
}
ll solve() {
ll l = 0, r = a[n];
while (l < r) {
ll mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l + t;
}
int main() {
FastIO
cin >> n >> m >> t;
for (int i = 1; i <= n; i ++) cin >> a[i];
sort(a + 1, a + n + 1);
for (int i = 1; i <= n; i ++) a[i] += a[i - 1];
while (m --) {
cin >> q;
cout << solve() << endl;
}
return 0;
}
D - 数组成鸡
参照验题人代码
int n, m;
int a[N];
set<int> st;
bool check(int x) {
ll res = 1;
for (int i = 0; i < n; i ++) {
res *= a[i] + x;
if (abs(res) > 1e9) return false;
}
st.insert(res);
return true;
}
string solve() {
int x; cin >> x;
return st.count(x) ? yes : no;
}
int main() {
FastIO
cin >> n >> m;
for (int i = 0; i < n; i ++) cin >> a[i];
sort(a, a + n);
st.insert(0);
for (int i = 0; i < n; i ++) {
if (i && a[i] == a[i - 1]) continue;
for (int l = -a[i] - 1; check(l); l --);
for (int r = -a[i] + 1; check(r); r ++);
}
while (m --) cout << solve() << endl;
return 0;
}
E - 本题又主要考察了贪心
题为贪心误导人,暴力枚举情况,复杂度为 O ( T × 3 n ) ≤ 6 × 1 0 6 O(T\times 3^n)\le6\times 10^6 O(T×3n)≤6×106
int n, m, res;
int a[N], c[N];
void dfs(int d = 0) {
if (d == m) {
for (int i = 1; i <= n; i ++) c[i] = a[i];
sort(c + 1, c + n + 1);
int t = upper_bound(c + 1, c + n + 1, a[1]) - c - 1;
t = n + 1 - t;
res = min(res, t);
return;
}
int u = b[d].aa, v = b[d].bb;
a[u] += 3;
dfs(d + 1);
a[u] -= 3;
a[v] += 3;
dfs(d + 1);
a[v] -= 3;
a[u] ++, a[v] ++;
dfs(d + 1);
a[u] --, a[v] --;
}
int solve() {
cin >> n >> m;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 0; i < m; i ++) cin >> b[i].aa >> b[i].bb;
res = n;
dfs();
return res;
}
F - 鸡数题!
第二类斯特林数
S ( n , m ) S(n,m) S(n,m) 表示的是把 n n n 个不同的小球放在 m m m 个相同的盒子里方案数,也记作 { n m } \begin{Bmatrix}n\\m\end{Bmatrix} {nm}
求法
- 递推 S ( n , m ) = S ( n − 1 , m − 1 ) + m S ( n − 1 , m ) S(n,m)=S(n−1,m−1)+mS(n−1,m) S(n,m)=S(n−1,m−1)+mS(n−1,m)
- 容斥 S ( n , m ) = 1 m ! ∑ k = 0 m ( − 1 ) k C ( m , k ) ( m − k ) n S(n,m)=\frac1{m!}\sum_{k=0}^m(-1)^kC(m,k)(m-k)^n S(n,m)=m!1∑k=0m(−1)kC(m,k)(m−k)n
性质
n k = ∑ i = 0 k S ( k , i ) × i ! × C ( n , i ) n^k=\sum_{i=0}^kS(k,i)×i!×C(n,i) nk=∑i=0kS(k,i)×i!×C(n,i)
ll n, m;
int qpow(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % mod;
a = (ll)a * a % mod;
b >>= 1;
}
return res;
}
int inv(int a) { return qpow(a, mod - 2); }
int solve() {
cin >> n >> m;
if (n < m) return 0;
ll res = 0;
vector<ll> fac(n + 1, 1), infac(n + 1, 1);
for (int i = 1; i <= n; i ++)
infac[i] = inv(fac[i] = fac[i - 1] * i % mod);
for (int i = 2; i <= m; i ++) res = res * inv(i) % mod;
for (int i = 0; i <= m; i ++) {
ll t = qpow(m - i, n) * infac[i] % mod * infac[m - i] % mod;
res = (res + mod + (i & 1 ? -1 : 1) * t) % mod;
}
return res;
}
G - why买外卖
前缀和即可
int n, m;
pii a[N];
ll solve() {
cin >> n >> m;
for (int i = 0; i < n; i ++) cin >> a[i].aa >> a[i].bb;
sort(a, a + n);
for (int i = 1; i < n; i ++) a[i].bb += a[i - 1].bb;
for (int i = n - 1; i >= 0; i --)
if (a[i].aa - m <= a[i].bb) return a[i].bb + m;
return m;
}
H - 01背包,但是bit
参照官方题解:
记所选物品重量或起来是 c c c,枚举 m m m 里是 1 1 1 的位,让 c c c 里该位为 0 0 0,则该位将 m m m 分成了两部分:
- 对于更高位,要求所选的物品这些位必须是 m m m 的子集(即 m m m 对应位是 1 1 1 才能选)
- 对于更低位,可以全为 1 1 1,没有任何限制
因此,枚举 m m m 每一位作为这个分界,每个物品就变成了要么能选要么不能选,所以把能选的都选上就好
int n, m;
int v[N], w[N];
ll solve() {
cin >> n >> m;
for (int i = 0; i < n; i ++) cin >> v[i] >> w[i];
ll res = 0;
auto check = [&](int x) {
ll ans = 0;
for (int i = 0; i < n; i ++)
if ((x & w[i]) == w[i]) ans += v[i];
res = max(res, ans);
};
for (int i = 29; i >= 0; i --)
if (m & 1 << i) check((m ^ 1 << i) | (1 << i) - 1);
check(m);
return res;
}
I - It’s bertrand paradox. Again!
概率分析,第一种方法是圆心概率一定 第二种是半径概率一定。因此第一个人的圆心位置概率更平均,答案不唯一,我大概意思一下,一发过了
int n, a, b;
string solve() {
cin >> n;
a = b = 0;
while (n --) {
int x, y, r; cin >> x >> y >> r;
x = max(abs(x), abs(y));
if (x <= 70) a ++;
else b ++;
}
if (1.0 * a / b > 1.2) return bb;
return aa;
}
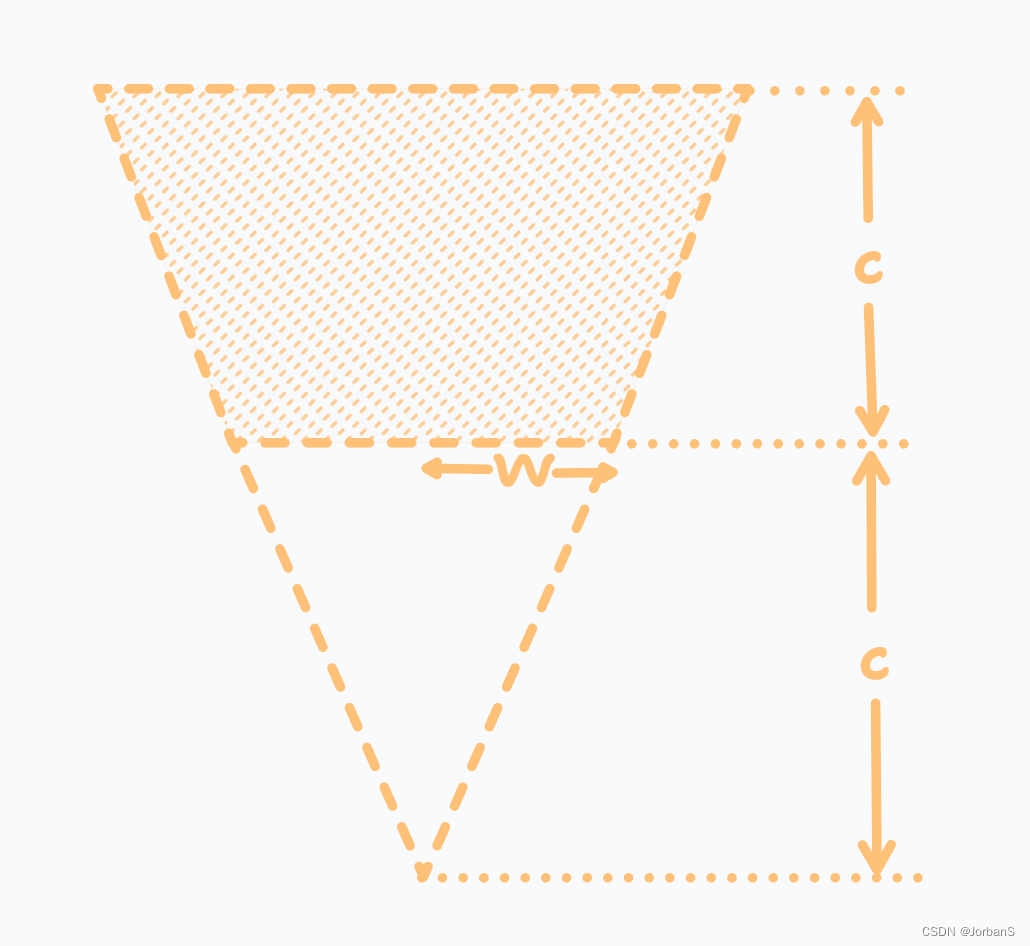
L - 要有光
计算阴影部分面积即可
double solve() {
double c, d, h, w; cin >> c >> d >> h >> w;
return c * w * 3;
}
M - 牛客老粉才知道的秘密
int solve() {
int n; cin >> n;
int res = n / 6;
return n % 6 ? res * 2 : res;
}