最新！2024顶级SCI优化！TTAO-CNN-BiGRU-MSA三角拓扑聚合优化、双向GRU融合注意力的多变量回归预测程序！

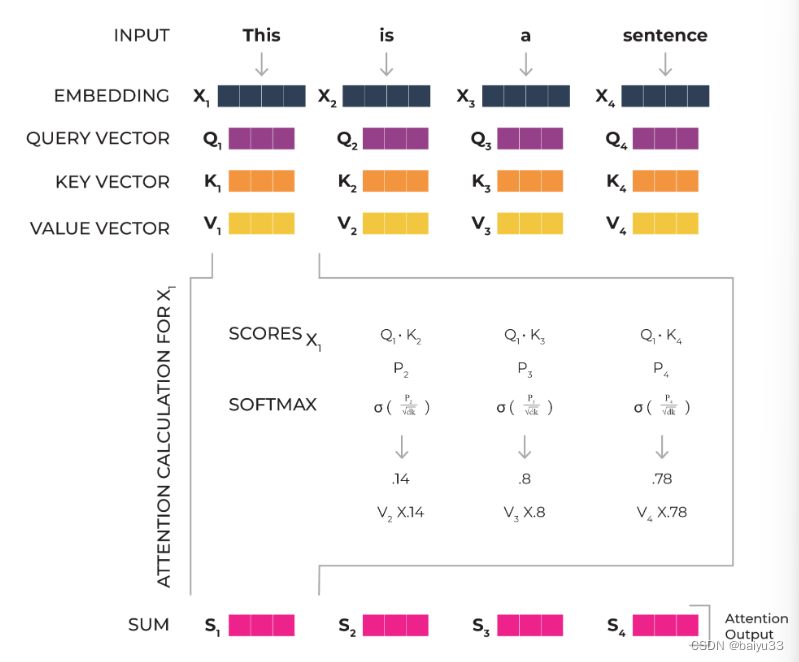
适用平台：Matlab 2023版及以上

TTOA三角聚合优化算法，将在2024年3月正式发表在中科院1区顶级SCI期刊《Expert Systems with Applications》上。

该算法提出时间极短，目前以及近期内不会有套用这个算法的文献。新年伊始，尽快拿下！

我们利用该创新性极高的优化算法对我们的CNN-BiGRU-Attention时序和空间特征结合-融合注意力机制的回归预测程序代码中的超参数进行优化，构成TTAO-CNN-BiGRU-MSA多变量回归预测模型.

文献解读：这个算法的启发来源是类似三角形的拓扑学性质。名为Triangulation Topology Aggregation Optimizer，TTAO）的新型数学元启发算法中，每个三角形拓扑单元表示一个搜索个体。TTAO算法通过聚合形成不同大小的类似三角形拓扑单元，以作为基本的进化单元。与其他元启发算法不同，TTAO算法提出了一种新的进化指导模式，主要依靠每个三角形单元中的最佳个体指导单元内个体的进化。因此，这种进化种群不仅依赖于全局引导的优秀个体，还吸收了每个单元中最佳个体的有效正向信息，有助于解决复杂优化问题，克服传统方法在全局搜索时进入局部极值的缺点。接下来，文章通过与其它对比算法：HHO ；SCSO；SAO；BWO；AOA等测试，验证了TTAO算法具有更强的收敛性能。在CEC2017函数和8个工程问题上评估了其优化性能。实验结果表明，TTAO算法在30维CEC2017函数上具有优越的收敛性和稳定性。

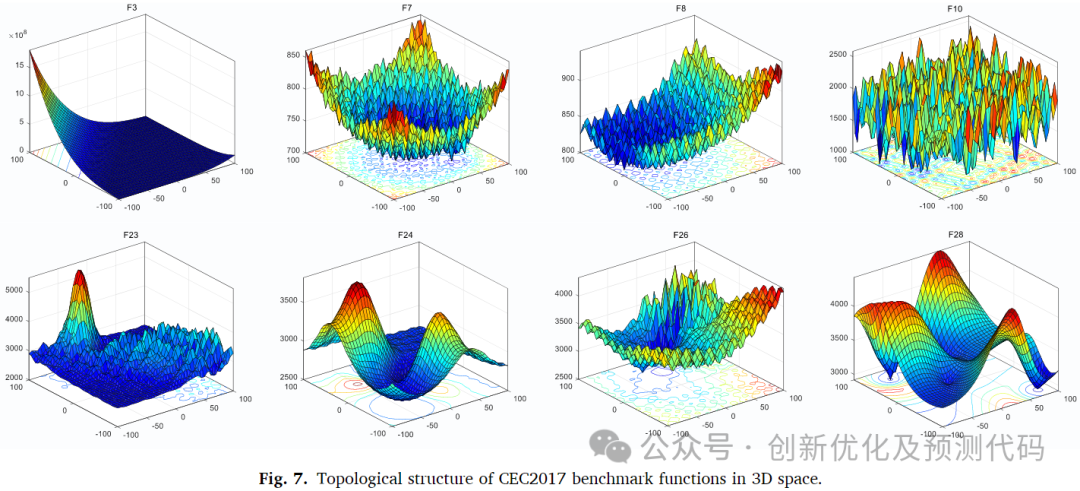
原理：许多领域通常将研究对象划分为三角形拓扑单元，并建立相关模型进行识别和分析：如金字塔，三角尺等。

在有限或无限维空间中，三角形拓扑可以被视为二维子空间的子图。与其他拓扑相比，三角形在某些封闭系统中更简单、更稳定。

TTAO算法主要通过以下两个阶段进行优化过程：

①不同单元之间的聚合
②相似三角形单元内的聚合

在这个过程中，不断在搜索空间中生成新的顶点，并用它们构建不同大小的相似三角形。TTAO算法将每个三角形视为具有四个个体的基本进化单元，即三角形的三个顶点和一个内部随机顶点。聚合的核心是将具有优良特性的顶点分组在一起。具体来说，TTAO算法通过聚合在不同拓扑单元之间或内部收集具有正向信息的顶点，不断构建相似三角形。

优化步骤：

算法通过迭代进化，在搜索空间中不断生成新的顶点，以构建不同大小的相似三角形。
每个三角形都被视为一个基本进化单元，包含四个搜索个体，即三角形的三个顶点和一个内部随机顶点。
TTAO算法的核心是聚集具有优越特性的顶点。具体而言，TTAO算法通过聚集来自不同拓扑单元的优秀个体信息，以创建新的可行解。
算法通过三个阶段的更新过程来实现全局搜索和局部挖掘：生成三角拓扑单元、通用聚集和局部聚集。

构成的TTAO-CNN-BiGRU-MSA多变量回归预测模型的创新性在于以下几点：

TTAO算法区别于传统智能算法的创新性：

①细胞聚类策略：TTAO 算法采用三角形拓扑单元展开优化过程，每个三角形拓扑单元具有一个顶点，这些顶点分别代表了搜索个体。这种细胞聚类策略使得 TTAO 算法能够更好地挖掘局部和全局信息。

②两级聚合策略：TTAO 算法采用了两级聚合策略：广义聚合和局部聚合。广义聚合主要关注全局探索，通过不同三角形拓扑单元间的信息交换来找到更有希望的位置；局部聚合则使得每个单元内的信息得到有效开发，确保准确地探索局部区域。

③自适应策略：TTAO 算法将上一代的有效信息自适应地继承下来，从而保持种群的多样性。这种自适应策略使得 TTAO 算法能够快速收敛到全局最优解。

④个体引导进化策略：TTAO算法提出了一种新的关键个体引导进化策略，使得该算法不仅依赖于精英个体的全局引导进化，还吸收了每个单元中最佳个体的积极正向信息。

优化套用—基于三角拓扑聚合优化算法（TTAO）、卷积神经网络（CNN）和双向门控循环单元网络(BiGRU)融合注意力机制（Multi-Head Self Attention，MSA）的超前24步多变量时间序列回归预测算法TTOA-CNN-BiGRU-MSA：

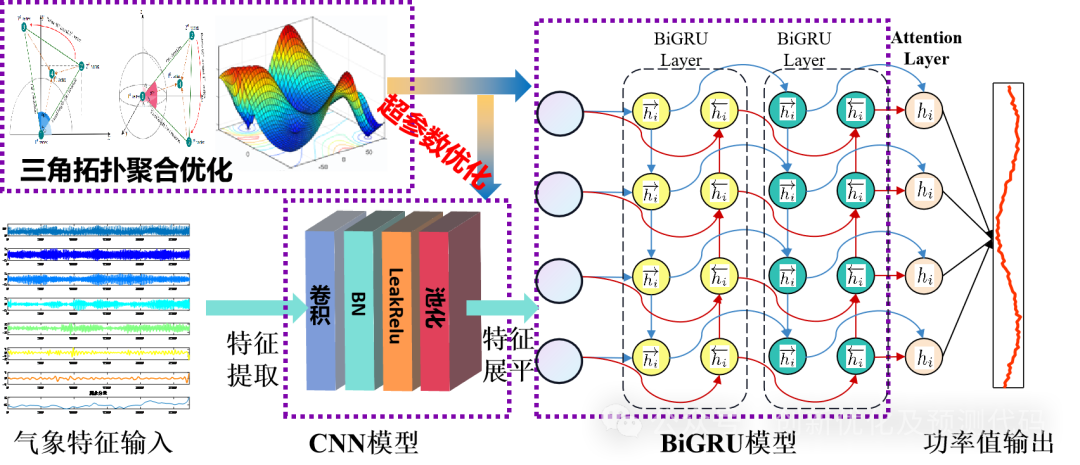
功能：

1、多变量特征输入，单序列变量输出，输入前一天的特征，实现后一天的预测，超前24步预测。

2、通过TTAO优化算法优化学习率、卷积核大小、神经元个数，这3个关键参数，以最小MAPE为目标函数。

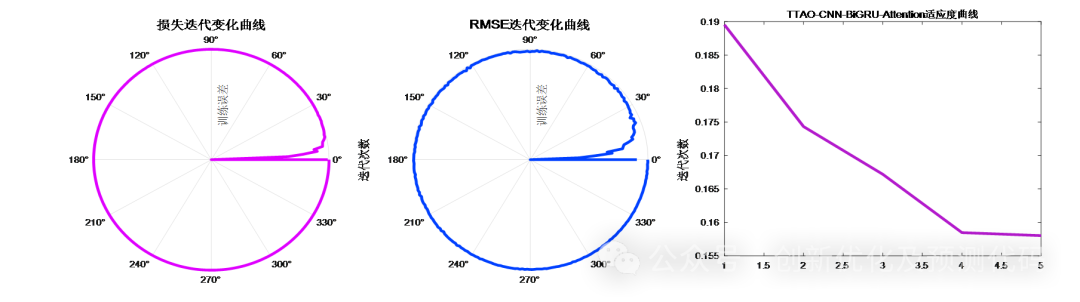
3、提供损失、RMSE迭代变化极坐标图；网络的特征可视化图；测试对比图；适应度曲线（若首轮精度最高，则适应度曲线为水平直线）。

4、提供MAPE、RMSE、MAE等计算结果展示。

适用领域：风速预测、光伏功率预测、发电功率预测、碳价预测等多种应用。

数据集格式：

前一天18个气象特征，采样时间为24小时，输出为第二天的24小时的功率出力，也就是18×24输入，1×24输出，一共有75个这样的样本。

预测值与实际值对比；训练特征可视化：

训练误差曲线的极坐标形式（误差由内到外越来越接近0）；适应度曲线（误差逐渐下降）

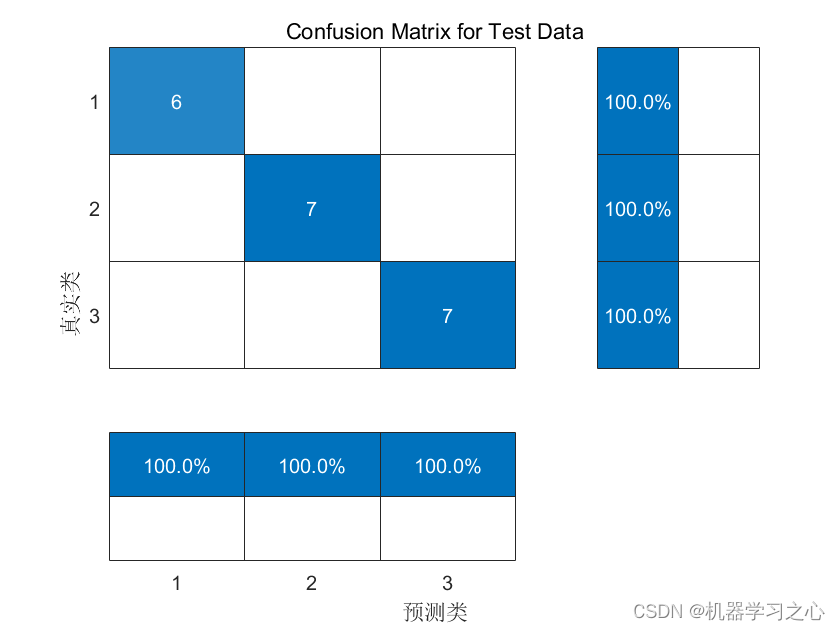
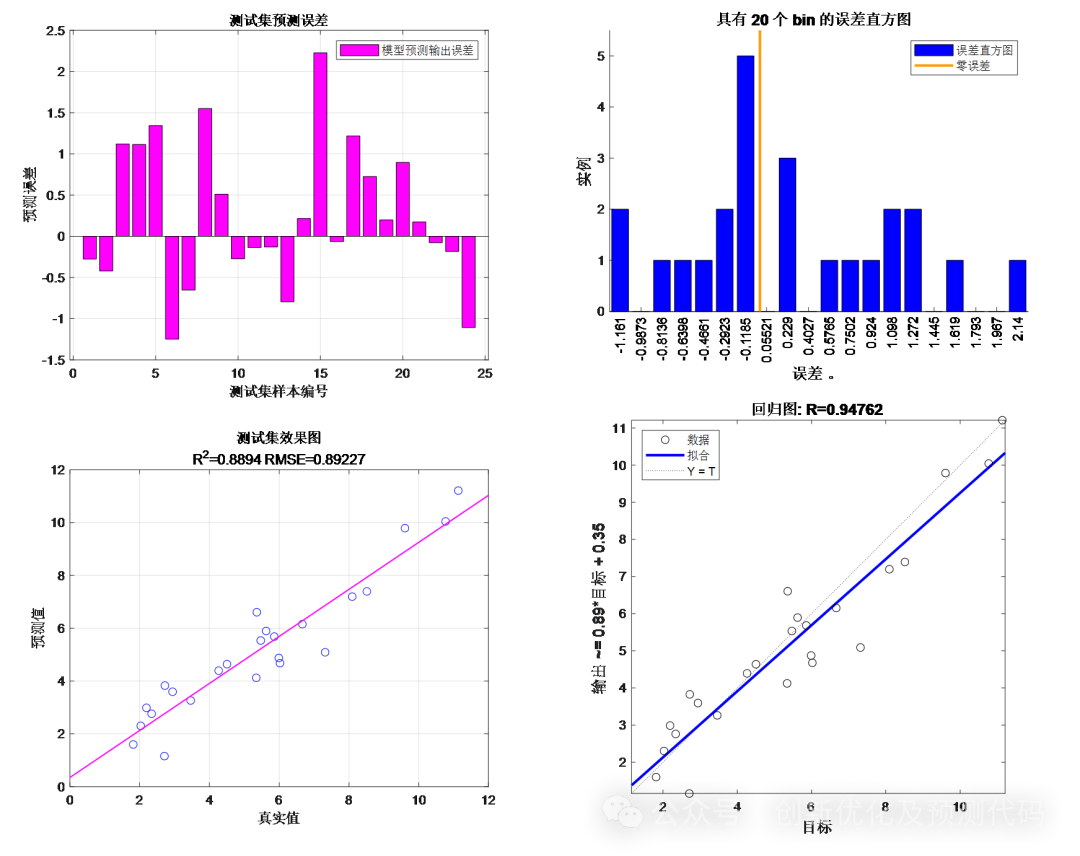
误差评估：

TTAO部分核心代码：

完整代码：https://mbd.pub/o/bread/ZZqZlZ1y
%  三角拓扑聚合优化器
function [fbest,Xbest,Convergence_curve,BestPred,bestNet,bestInfo]=TTAOtest(PopSize,T,Low,Up,Dim,fobj)

N=floor(PopSize/3); % 初始化N/3个个体。
X1=rand(N,Dim).*(Up-Low)+Low;
t=1;
while t<T+1
    %% 形成三角拓扑单元
    l=9*exp(-t/T);% 三角拓扑单元的大小。
    for i=1:N
        theta=rand(1,Dim)*pi;
        h1=cos(theta);
        h2=cos(theta+pi/3);
        X2(i,:)=X1(i,:)+l*h1;
        X3(i,:)=X1(i,:)+l*h2;
    end
    X2 = max(X2,Low);
    X2 = min(X2,Up);
    X3 = max(X3,Low);
    X3 = min(X3,Up);
    r1=rand;r2=rand;
    X4=r1*X1+r2.*X2+(1-r1-r2)*X3;
    X4 = max(X4,Low);
    X4 = min(X4,Up);
    for i=1:N
        [X1_fit(i), value1{i},Net1{i},Info1{i}] =fobj(X1(i,:));
        [X2_fit(i), value2{i},Net2{i},Info2{i}] =fobj(X2(i,:));
        [X3_fit(i), value3{i},Net3{i},Info3{i}] =fobj(X3(i,:));
        [X4_fit(i), value4{i},Net4{i},Info4{i}] =fobj(X4(i,:));
    end
    X=[X1 X2 X3 X4];
    fit=[X1_fit;X2_fit;X3_fit;X4_fit];
    value = [value1; value2; value3; value4];
    Net = [Net1; Net2; Net3; Net4];
    Info = [Info1; Info2; Info3; Info4];

    [X_sort,index]=sort(fit);
    %% 在每个三角拓扑单元中找到最优点和次优点。
    for i=1:N
        X_best_1(i,:)=X(i,(index(1,i)-1)*Dim+1:index(1,i)*Dim);
        X_best_2(i,:)=X(i,(index(2,i)-1)*Dim+1:index(2,i)*Dim);
    end
    best_fit_1=X_sort(1,:);
    best_fit_2=X_sort(2,:);

    sorted_value(:, 1) = value(index(:, 1), 1);
    sorted_value(:, 2) = value(index(:, 2), 2);
    best_value_1 = sorted_value(1,:);
    best_value_2 = sorted_value(2,:);

    sorted_Net(:, 1) = Net(index(:, 1), 1);
    sorted_Net(:, 2) = Net(index(:, 2), 2);
    best_Net_1 = sorted_Net(1,:);
    best_Net_2 = sorted_Net(2,:);

    sorted_Info(:, 1) = Info(index(:, 1), 1);
    sorted_Info(:, 2) = Info(index(:, 2), 2);
    best_Info_1 = sorted_Info(1,:);
    best_Info_2 = sorted_Info(2,:);

    %% 通用聚合
    for i=1:N
        r=rand(1,Dim);
        X_new=X_best_1;
        X_new(i,:)=[];
        l1=randi(N-1);
        X_G(i,:)=(r.*X_best_1(i,:)+(ones(1,Dim)-r).*X_new(l1,:));
        X_G(i,:) = max(X_G(i,:),Low);
        X_G(i,:) = min(X_G(i,:),Up);
        [X_fit_G(i), valueG{i},NetG{i},InfoG{i}]=fobj(X_G(i,:));
        if X_fit_G(i)<best_fit_1(i)
            X_best_1(i,:)=X_G(i,:);
            best_fit_1(i)=X_fit_G(i);
            best_value_1{i}=valueG{i};
            best_Net_1{i}=NetG{i};
            best_Info_1{i}=InfoG{i};

        elseif X_fit_G(i)<best_fit_2(i)
            X_best_2(i,:)=X_G(i,:);
            best_value_2{i}=valueG{i};
            best_Net_2{i}=NetG{i};
            best_Info_2{i}=InfoG{i};
        end
    end
    %% 局部聚合
    for i=1:N
        a=(exp(1)-(exp(1))^3)/(T-1);
        b=(exp(1))^3-a;
        alpha=log(a*t+b);
        X_C(i,1:Dim)=X_best_1(i,1:Dim)+alpha*(X_best_1(i,1:Dim)-X_best_2(i,1:Dim));
        X_C(i,:) = max(X_C(i,:),Low);
        X_C(i,:) = min(X_C(i,:),Up);
        [X_fit_C(i), valueC{i},NetC{i},InfoC{i}]=fobj(X_C(i,:));
        if X_fit_C(i)<best_fit_1(i)
            X_best_1(i,:)=X_C(i,:);
            best_fit_1(i)=X_fit_C(i);
            best_value_1{i}=valueC{i};
            best_Net_1{i}=NetC{i};
            best_Info_1{i}=InfoC{i};
        end
    end
    %% 
    N00=PopSize-N*3;
    if N00~=0
        X00=rand(PopSize-N*3,Dim).*(Up-Low)+Low;
        for i=1:N00
            [X00_fit,value00{i},Net00{i},Info00{i}]=fobj(X00(i,:));
        end
        X_1_0=[X_best_1;X00];
        X_1_0_fit=[best_fit_1,X00_fit];
        value_1_0=[best_value_1;value00];
        Net_1_0=[best_Net_1;Net00];
        Info_1_0=[best_Info_1;Info00];
        
        [~,index01]=sort(X_1_0_fit);
        X_best_1=X_1_0(index01(1:N),:);
        best_value_1=value_1_0(index01(1:N),:);
        best_Net_1=Net_1_0(index01(1:N),:);
        best_Info_1=Info_1_0(index01(1:N),:);

        best_fit_1=X_1_0_fit(index01(1:N));
    end
    X1=X_best_1;
    %% 前N/3个个体作为下一次迭代的初始种群。

部分图片来源于网络，侵权联系删除！

欢迎感兴趣的小伙伴“复制代码上方链接”或“联系小编”获得完整版代码哦~，关注小编会继续推送更有质量的学习资料、文章程序代码~