目录
1. 二进制中 1 的个数
1.1 题目描述
1.2 可能引起错误的解法
1.3 常规解法
1.4 思路优化
1. 二进制中 1 的个数
原题链接:
剑指 Offer 15. 二进制中1的个数 - 力扣(LeetCode)
https://leetcode.cn/problems/er-jin-zhi-zhong-1de-ge-shu-lcof/
1.1 题目描述
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为 汉明重量).)。
1.2 可能引起错误的解法
基本思路: 先判断整数二进制表示中最右边的一位是不是1, 接着把输入的整数右移一位, 此时原来处于从右边数起的第二位被移到最右边了, 再判断是不是1, 就这样每次移动一位, 直到整个整数变为0为止. 现在的问题就是如何判断一个整数的最右边的二进制位是不是1. 显然我们只需要把整数和1做按位与运算看结果是不是0就可以了. 因为整数1的最右边的二进制位是1, 其余全是0. 如果一个整数与 1 做按位与运算的结果是 1 则说明该整数的最右边的二进制位是1, 反之则是 0 .

整数右移一位和把整数除以2在数学上是等价的, 那我们能将右移运算换成除法运算吗?
注意: 在编程中移位运算的效率是要比乘除法要高一点点的, 在实际编程中应尽可能地用移位运算代替乘除运算.
我们知到右移是分为算数右移和逻辑右移.
算数右移: 最右边的二进制位丢弃, 左边补原符号位(整数补0, 负数补1).
逻辑右移: 最右边的二进制位丢弃, 左边补0.
那我们程序中的 >> 是算数右移还是逻辑右移嘞, 我们可以用 -1 这个数来分析一波:

通过代码来测试结果即可:
#include<stdio.h>
int main()
{
int a = -1;
a >>= 1;
printf("%d", a);
return 0;
}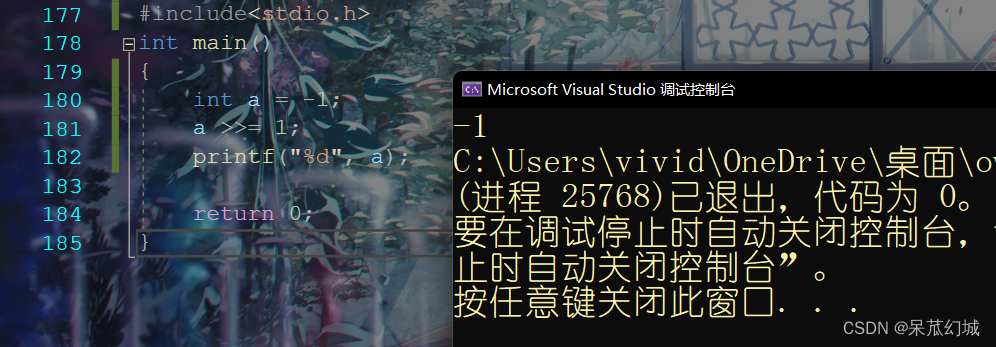
我们知道 >> 为算数右移时, 问题就显现出来了, 如果输入的整数是一个负数, 那么对该整数进行右移就会陷入死循环(无限地补符号位1嘛).
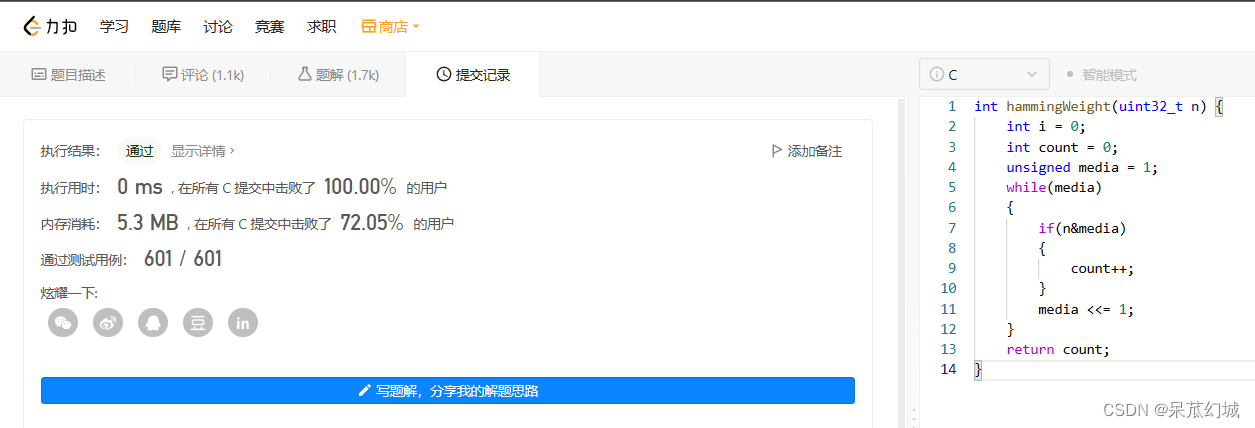
1.3 常规解法
为了避免死循环, 我们不能右移输入的整数, 但是我们可以把与该整数进行按位与操作的 1 逐步左移, 直到 1 左移到为 0 时结束循环.

int hammingWeight(uint32_t n) {
int i = 0;
int count = 0;
unsigned media = 1;
while(media)
{
if(n&media)
{
count++;
}
media <<= 1;
}
return count;
}
1.4 思路优化
在优化之前, 我们先来分析一个二进制数减 1 的情况. 如果一个整数不等于0, 那么该整数的二进制表示中至少有一位是 1 . 假设这个数的最右边一位是 1 , 那么减去 1 时, 最后一位变成 0 而其它位保持不变.
接下来讨论最后一位不是 1 的情况: 如果该整数的二进制表示中最右边的 1 位于第 m 位, 那么减去 1 时, 第 m 位由 1 变成 0 , 而第 m 位之后的 0 都变成 1 , 整数中第 m 位之前的所有位保持不变. 例如对于二进制序列 1100, 它的第二位(最开始是第0位嘛)是最右边的 1 . 减去 1 之后, 第二位变成 0 , 他后面的两位变成 1 , 而前面的 1 保持不变, 结果是 1011 (相当于把该整数二进制表示中的最右边的1和后面的二进制位取反了) .
接下来我们把 1100 减 1 的结果1011与原数 1100 做按位与的运算 得到结果: 1000 就将原来的整数的最右边的1给去掉了.
于是我们得到一个重要的结论: 把一个整数减去 1 之后再和原来的E整数做按位与运算, 得到的结果相当于把整数的二进制表示中最右边的 1 变成 0 .
其实很好理解: 整数减 1 就相当于把该整数二进制表示中的最右边的1和后面的二进制位取反了, 在去与原数按位与, 当然抹去了最右边的 1 嘛 (不相同的两个二进制位做按位与得到的是0嘛).
int hammingWeight(uint32_t n) {
int count = 0;
while(n)
{
count++;
n = (n-1)&n;
}
return count;
}