排序之计数排序

news2024/11/27 4:30:12

꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好，我是xiaoxie.希望你看完之后,有不足之处请多多谅解，让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页：xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
系列专栏：xiaoxie的JAVA系列专栏——CSDN博客●'ᴗ'σσணღ*
我的目标:"团团等我💪( ◡̀_◡́ ҂)"

( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注（互三必回）!

一.计数排序概念

计数排序是一种非比较性的排序算法，它的基本思想是通过统计一个数组中每个元素出现的次数，然后根据这个统计信息将数组中的元素按照顺序排列这个方法待排序数组的范围不是很大且元素都是非负整数的情况下，具有较高的排序效率。

1.过程

1.找出待排序的数组中最大和最小的元素

2.统计数组中每个值为i的元素出现的次数，存入数组C的第i项

3.对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）

4.反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

2.图解过程

如下图，A为待排序的数组，C记录A中各个值的数目。

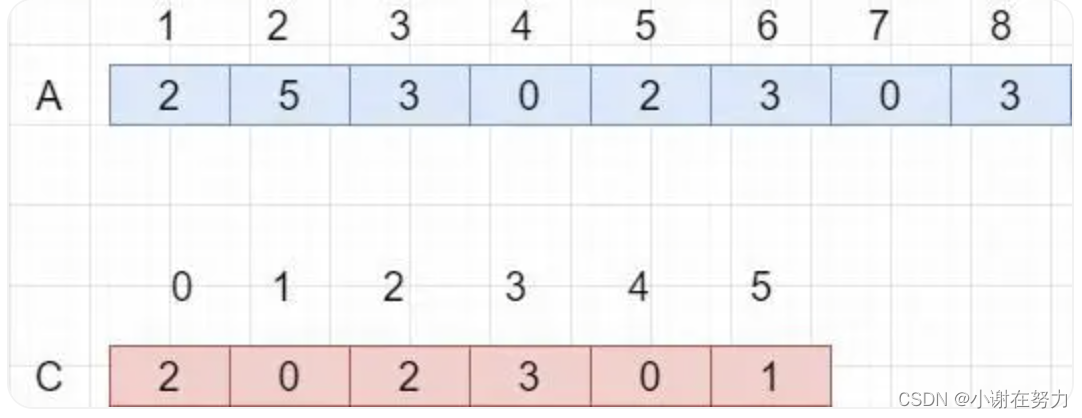
将C[i]转换为值小于等于i的元素个数。

为数组A从后向前的每个元素找到对应的B中的位置，每次从A中复制一个元素到B中，C中相应的计数减一。

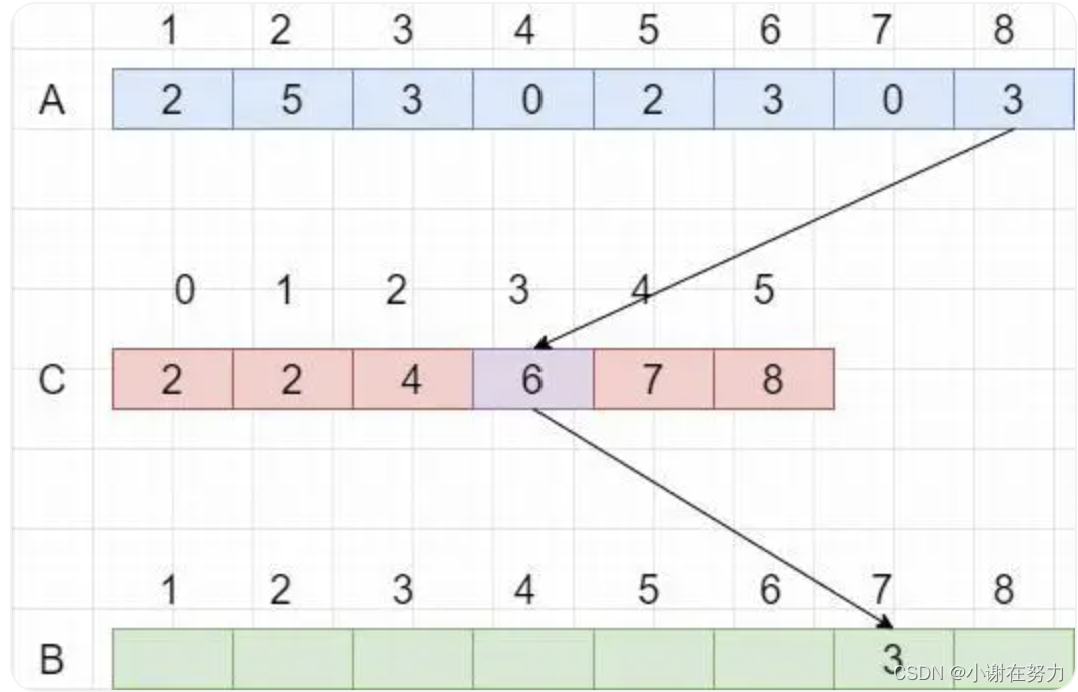
当A中的元素都复制到B中后，B就是排序好的结果，如图所示

3.代码

1.Java版本

  public static void countSort(int[] array) {
        //1.求最值 -> O(n)
        int min = array[0];
        int max = array[0];
        for (int i = 1; i < array.length; i++) {
            if(min > array[i]) {
                min = array[i];
            }
            if(max < array[i]) {
                max = array[i];
            }
        }
        //2、定义计数数组 进行初始化   -> O(n)
        int[] count = new int[max-min+1];

        for (int i = 0; i < array.length; i++) {
            int index = array[i]-min;
            count[index]++;
        }

        //3、遍历计数数组   -> O(max-min) ：max-min-》范围
        int k = 0;//表示array数组的下标
        for (int i = 0; i < count.length; i++) {
            while (count[i] != 0) {
                array[k] = i + min;
                k++;
                count[i]--;
            }
        }
    }

2.C++版本

#include <iostream>
using namespace std;

void countSort(int array[], int n) {
    // 1. 求最值 -> O(n)
    int min = array[0];
    int max = array[0];
    for (int i = 1; i < n; i++) {
        if (min > array[i]) {
            min = array[i];
        }
        if (max < array[i]) {
            max = array[i];
        }
    }

    // 2、定义计数数组 进行初始化   -> O(n)
    int count[max - min + 1] = {0};

    for (int i = 0; i < n; i++) {
        int index = array[i] - min;
        count[index]++;
    }

    // 3、遍历计数数组   -> O(max - min)
    int k = 0; // 表示array数组的下标
    for (int i = 0; i < count.size(); i++) {
        while (count[i] != 0) {
            array[k] = i + min;
            k++;
            count[i]--;
        }
    }
}

4.时间复杂度

计数排序的时间复杂度为O(n+k)，其中n是待排序数组的大小，k是待排序数组中的最大值减最小值加1（即数组的取值范围）。计数排序的时间复杂度是线性的，不受待排序数组的分布情况的影响。但是，计数排序只适用于整数排序且取值范围不大的情况，对于较大范围的整数排序，计数排序的空间复杂度会较高，不适用于大规模数据的排序。