C++入门
- 1 内联函数
- 1.1 定义
- 1.2 查看方式
- 1.3 注意
- Thanks♪(・ω・)ノ谢谢阅读
- 下一篇文章见!!!
1 内联函数
1.1 定义
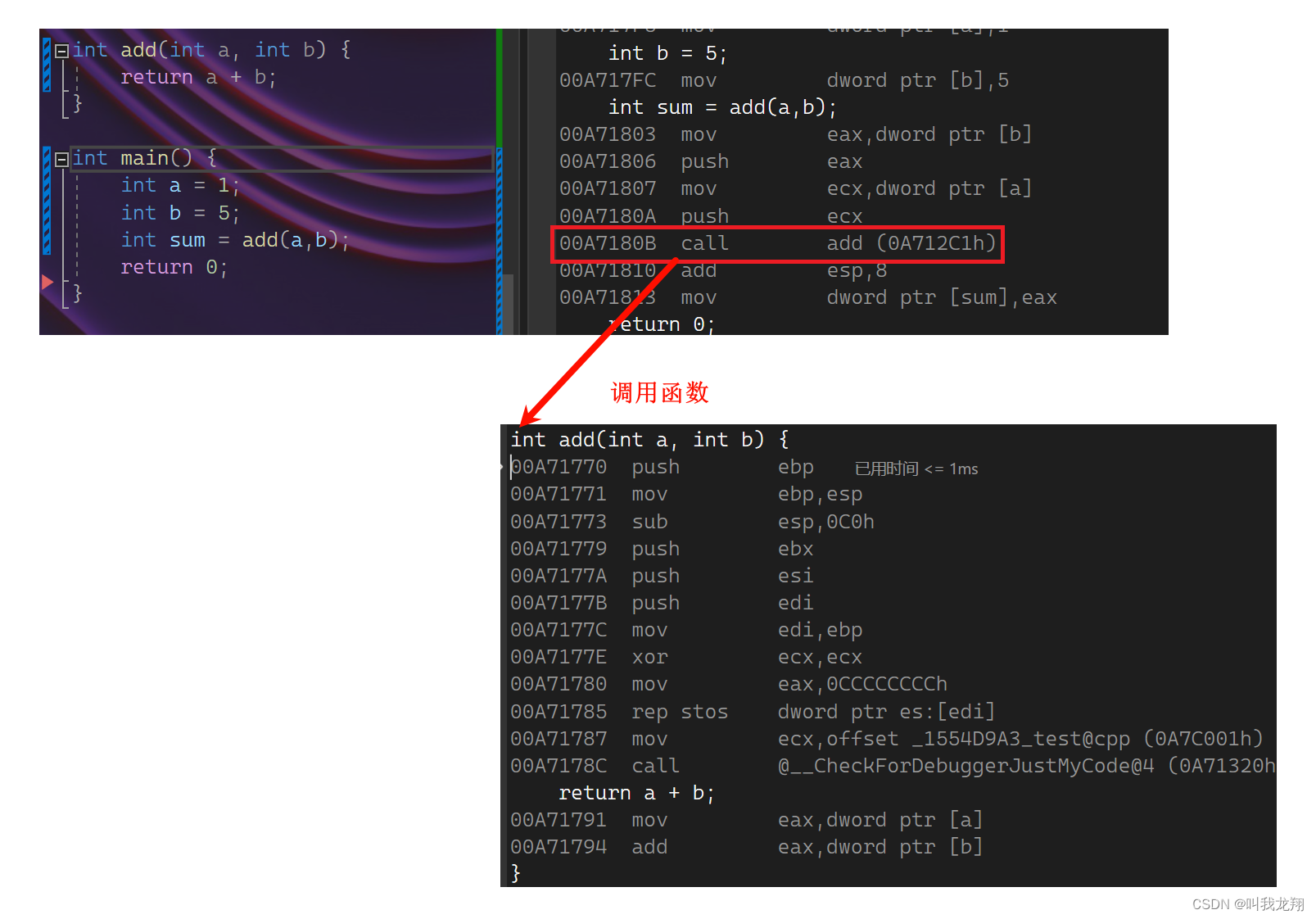
程序在执行一个函数前需要做准备工作:要将实参、局部变量、返回地址以及若干寄存器都压入栈中,然后才能执行函数体中的代码;函数体中的代码执行完毕后还要清理,将之前压入栈中的数据都出栈,然后接着执行函数调用位置以后的代码。
在函数较大时,执行函数需要较多时间,那么函数调用的时间可以忽略不计,
但是当函数较小时(比如求和,交换等简单函数),函数调用的时间就不可以忽略了。再加上如果频繁调用,那么就会有大部分时间花在函数调用上。
而内联函数是直接把函数加入其中,免去调用的时间开销。
以inline修饰的函数叫做内联函数,编译时C++编译器会在调用内联函数的地方展开,没有函数调 用建立栈帧的开销,内联函数提升程序运行的效率。
类似于C语言中的宏展开(宏的缺陷较多)。
1.2 查看方式
查看方式:
- 在release模式下,查看编译器生成的汇编代码中是否存在call Add
- 在debug模式下,需要对编译器进行设置,否则不会展开(因为debug模式下,编译器默认不会对代码进行优化,以下给出 vs2022 的设置方式)
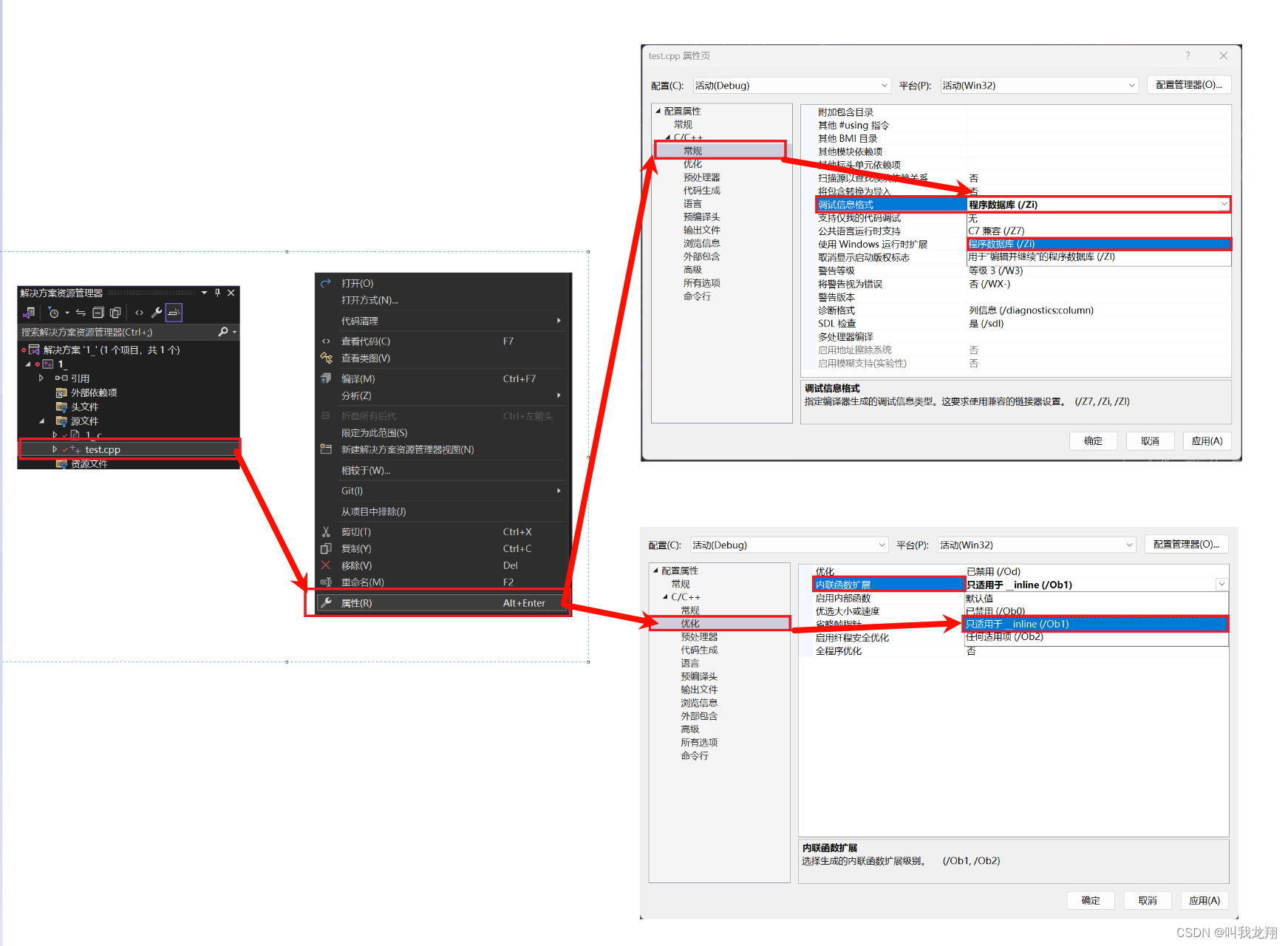
这下就可以看出内敛函数的优化了,如下:直接把函数插入 其中。
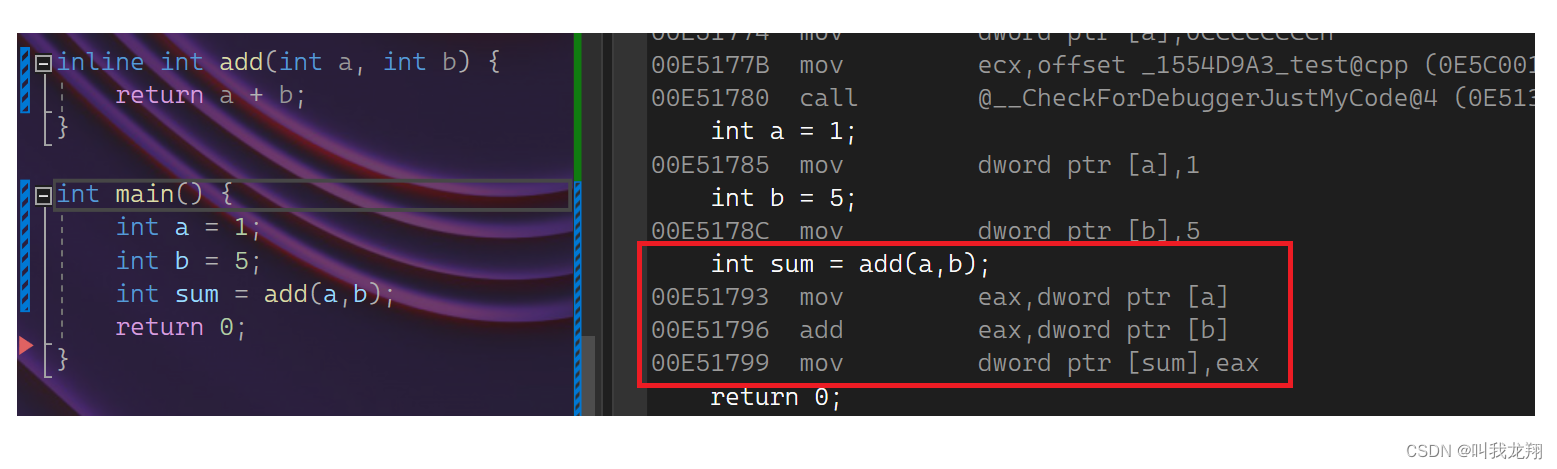
1.3 注意
- inline是一种以空间换时间的做法,如果编译器将函数当成内联函数处理,在编译阶段,会用函数体替换函数调用,缺陷:可能会使目标文件变大,优势:少了调用开销,提高程序运行效率。
- inline对于编译器而言只是一个建议,不同编译器关于inline实现机制可能不同,一般建议:
将函数规模较小(即函数不是很长,具体没有准确的说法,取决于编译器内部实现)、不是递归、且频繁调用的函数采用inline修饰,否则编译器会忽略inline特性。
《C++prime》第五版关于inline的建议:
内联说明只是向编译器发出请求,编译器可以选择忽略这个请求。 - inline不建议声明和定义分离,分离会导致链接错误。因为inline被展开,就没有函数地址了,链接就会找不到。
不可忽略的一点是:
代码膨胀,我们本身是1万行的主函数,如果有个 1万 行的函数,调用了100次。
使用内联函数: 结果是展开100次,我们的代码编译后就会变成100万行
不使用内联函数:函数会在栈区开辟空间,100次调用同一位置的函数,我们的代码是 2 万行
这样差距还是很大的。