C++不知算法系列之迷宫问题中的“见山不是山”

news2024/11/29 5:34:56

1. 前言

迷宫问题是一类常见的问题。

初识此类问题，应该是“见山是山”，理解问题的原始要求，便是查找从起点到终点的可行之路。

有了广泛的知识体系之后，应该是"见山不是山"。会发现迷宫就是邻接矩阵，树和图中顶点的关系常用邻接矩阵描述，所以，迷宫问题可以转化为树、图的搜索问题。或帮助理解树和图，反之也可在迷宫问题中用树、图中的理论。

最后便是“见山还是山”，能透过问题的表象，深化问题的本质，识破披着各色外衣的迷宫问题。

本文从不同的角度、全方位讲透迷宫问题中的“见山不是山”，让大家对迷宫问题有实质性的理解。

2. 迷宫问题

问题描述：

如下图迷宫地图中，1表示障碍物，0表示可通行。要求从起始点(0,0)出发，检查是否有行之有效的通路，可以一直走到终点(8,8)。迷宫问题的本质就是邻接矩阵的路径搜索问题。

常用的是广度优先和深度优先搜索算法。

1.png

2.1 设计数据类型

首先分析迷宫问题中的数据类型。

  • 坐标类型：用来描述迷宫中每个单元格的位置。
/*
*坐标类型
*/
struct Position {
	//x坐标
	int x;
	//y坐标
	int y;
	Position() {}
	//构造函数
	Position(int x,int y) {
		this->x=x;
		this->y=y;
	}
	//重载 == 运算符
	bool operator==(Position pos) {
		return this->x==pos.x && this->y==pos.y;
	}
    //输出
	void desc() {
		cout<<"(x:"<<x<<",y:"<<y<<")"<<"->";
	}
};
  • 方向类型：描述与每个单元格相邻的上、下、左、右 4 个单元格的关系。
/*
* 方向增量
*/
struct Direction {
	//x 方向增量
	int xOffset;
	//y 方向增量
	int yOffset;
};
  • 迷宫类：描述迷宫本身以及迷宫相对应的操作函数。
class Maze {
	private:
		//一般用二维数组存储迷宫信息
		int maze[10][10]= {
			{1,1,1,1,1,1,1,1,1,1},
			{1,0,0,1,0,1,1,1,1,1},
			{1,1,0,1,0,0,1,1,1,1},
			{1,1,0,1,0,0,0,0,1,1},
			{1,1,0,0,0,0,1,0,1,1},
			{1,1,1,1,0,0,1,0,1,1},
			{1,1,0,0,0,0,1,0,1,1},
			{1,1,1,1,0,0,1,0,1,1},
			{1,1,0,0,0,1,1,0,0,1},
			{1,1,1,1,1,1,1,1,1,1},
		};
		//地图中非障碍点，即值为 0 位置的个数
		int count=32;
		//当前坐标与相邻(右、下、左、上)坐标的增量关系
		Direction dirs[4]= { {0,1},{1,0},{0,-1},{-1,0} };
		//栈，用于深度搜索
		stack<Position> mazeStack;
		//队列，用于广度搜索
		queue<Position>  mazeQueue;
		//总路径数
		int totalCount=0;
	public:
        //构造函数
		Maze() {}
		/*
		*洪水填充算法检查迷宫的连通性
		*/
		void floodfill(Position start,Position end);
		/*
		* 是否连通
		*/
		void isConnection();
		/*
		* 非递归实现路径的查找
		* 只保证查找到路径
		* 需要借助栈
		*/
		void searchPathByStack(Position start,Position end);
		/*
		*  显示到深度搜索到的路径
		*/
		void showPath();
		/*
		*递归深度搜索
		*/
		bool searchPathByRecursion(Position start,Position end,int deep);
		/*
		*广度搜索
		*/
		void searchPathByQueue(Position start,Position end);
		/*
		* 显示地图
		*/
		void showMap() {
			cout<<"\n\t----------------------地图----------------------\n"<<endl;
			for(int i=0; i<10; i++) {
				for( int j=0; j<10; j++ )
					cout<<this->maze[i][j]<<"\t";
				cout<<endl;
			}
			cout<<"\n\t--------------------------------------------"<<endl;
		}
};

2.2 检查连通性

使用洪水填充算法检查迷宫的连通性。

洪水填充算法类似于古时候的"连坐法"，或说星星之火可以燎原也，从最初给定的位置开始，以蔓延之势，用-1填充与之相邻且值为 0的单元格。 本文中， -1和0都用于表示迷宫中的非障碍物区间。

洪水填充算法和后面的递归搜索算法相似，不同地方之处，洪水填充会蔓延至所有满足条件的位置，搜索则是强调到通向目标的路径。

/*
* 洪水填充算法检查迷宫的连通性
*/
void Maze::floodfill(Position start,Position end) {
	Position tmpPos;
	//检查起始点周边的点是否存在
	for(int i=0; i<4; i++ ) {
		//当前点上、下、左、右的相邻点
		tmpPos.x=start.x+ dirs[i].xOffset;
		tmpPos.y=start.y+dirs[i].yOffset;
		if( maze[tmpPos.x][tmpPos.y]==0 ) {
			//可通，则填充为 -1
			maze[tmpPos.x][tmpPos.y]=-1;
			//计数
			count--;
             //递归调用
			Maze::floodfill(tmpPos,end);
		}
	}
}

连通性结论：

/*
* 如果洪水填充算法所填充的单元格数量和初始时值为 0 的单元格的数量一样，则连通
*/
void Maze::isConnection() {
	if(Maze::count==0)
		cout<<"地图是连通!"<<endl;
	else
		cout<<"地图不是连通的!"<<endl;
}

测试：

//需要的所有头文件
#include <iostream>
#include <stack>
#include <vector>
#include <queue>
using namespace std;
int main(int argc, char** argv) {
	Maze maze;
	//起点位置
	Position startPos(1,1);
	//终点位置
	Position  endPos(8,8);
	cout<<"洪水填充算法前的地图"<<endl;
	maze.showMap();
	//洪水填充算法
	maze.floodfill(startPos,endPos);
	cout<<"洪水填充算法后的地图"<<endl;
	maze.showMap();
	//结论
	maze.isConnection();
	return 0;
}

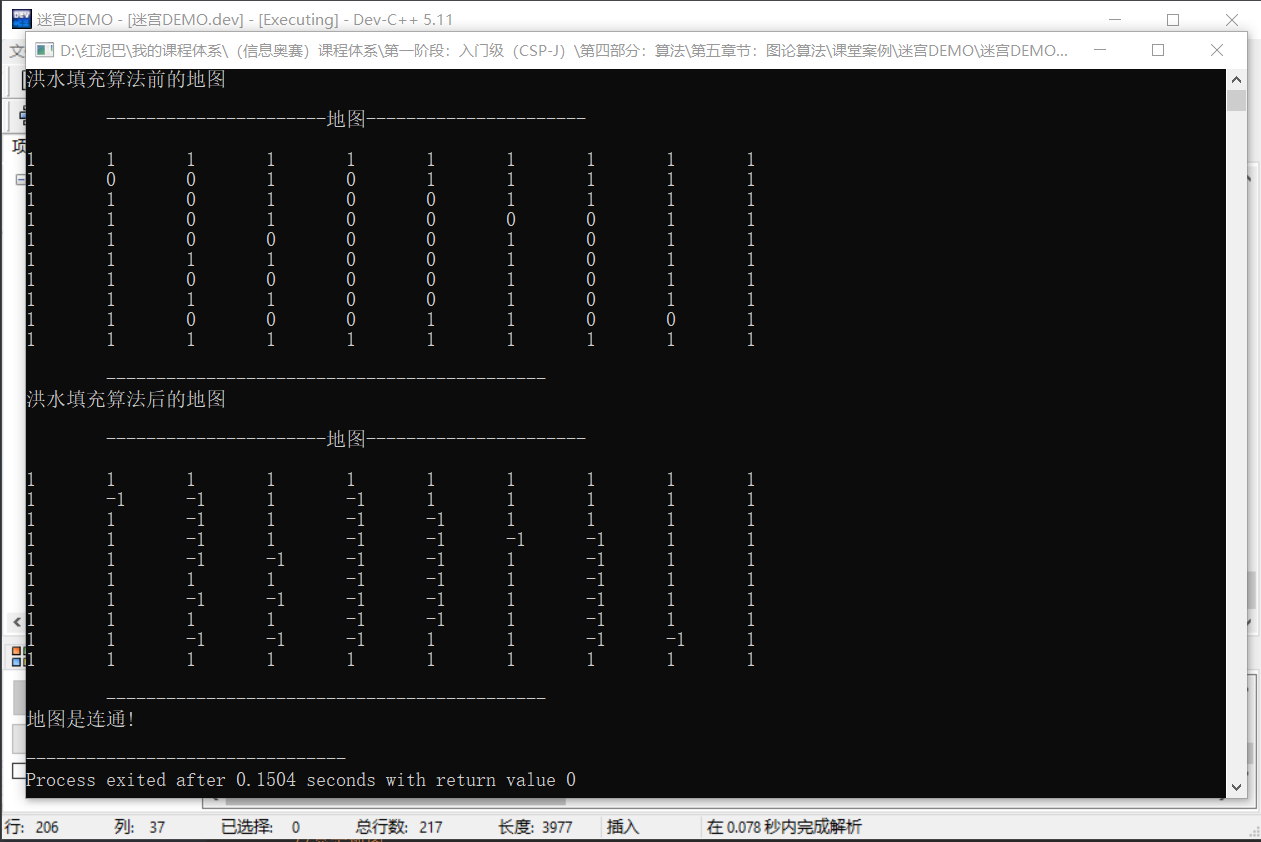
输出结果： 迷宫中值为0的位置全部被-1填充。

2.png

2.3 深度搜索

深度搜索可以使用非递归和递归 2 种方案实现。

2.3.1 非递归的思想

非递归深度搜索需要借助栈。

  • 初始，把起始点的坐标值压入栈中。

3.png

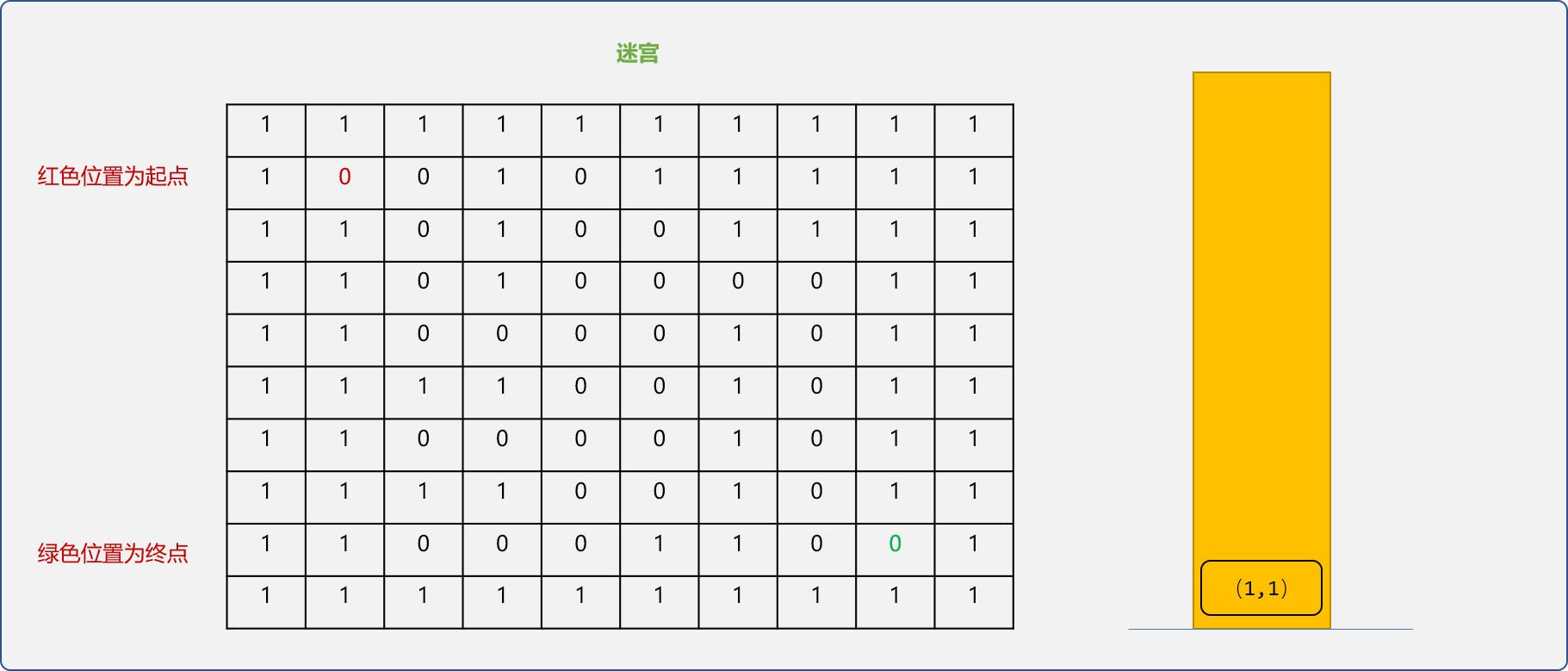
  • 获取栈顶的坐标，检查此坐标的上、下、左、右 4 个相邻的坐标是否可通行。如果可通行，则压入栈中，且标识此坐标已经访问过。如下图使用绿色表示已经访问过。

4.png

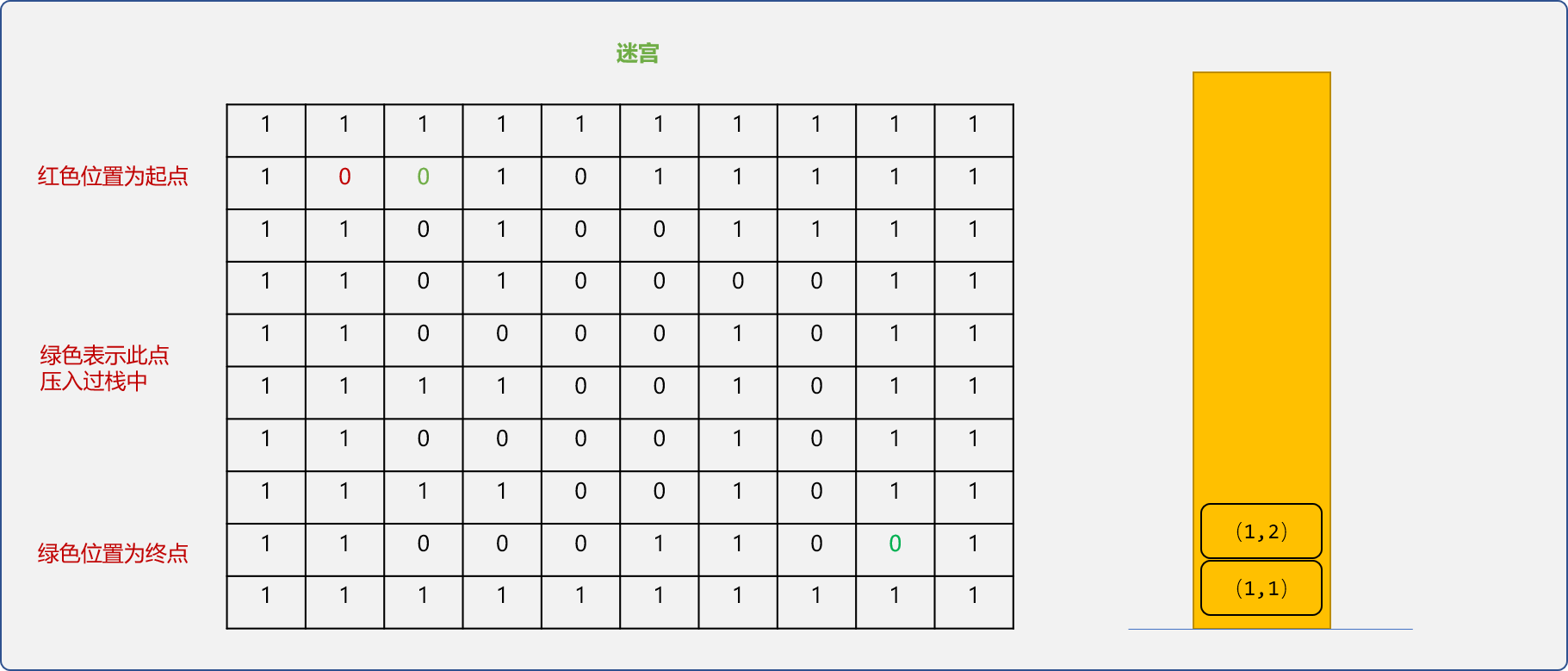
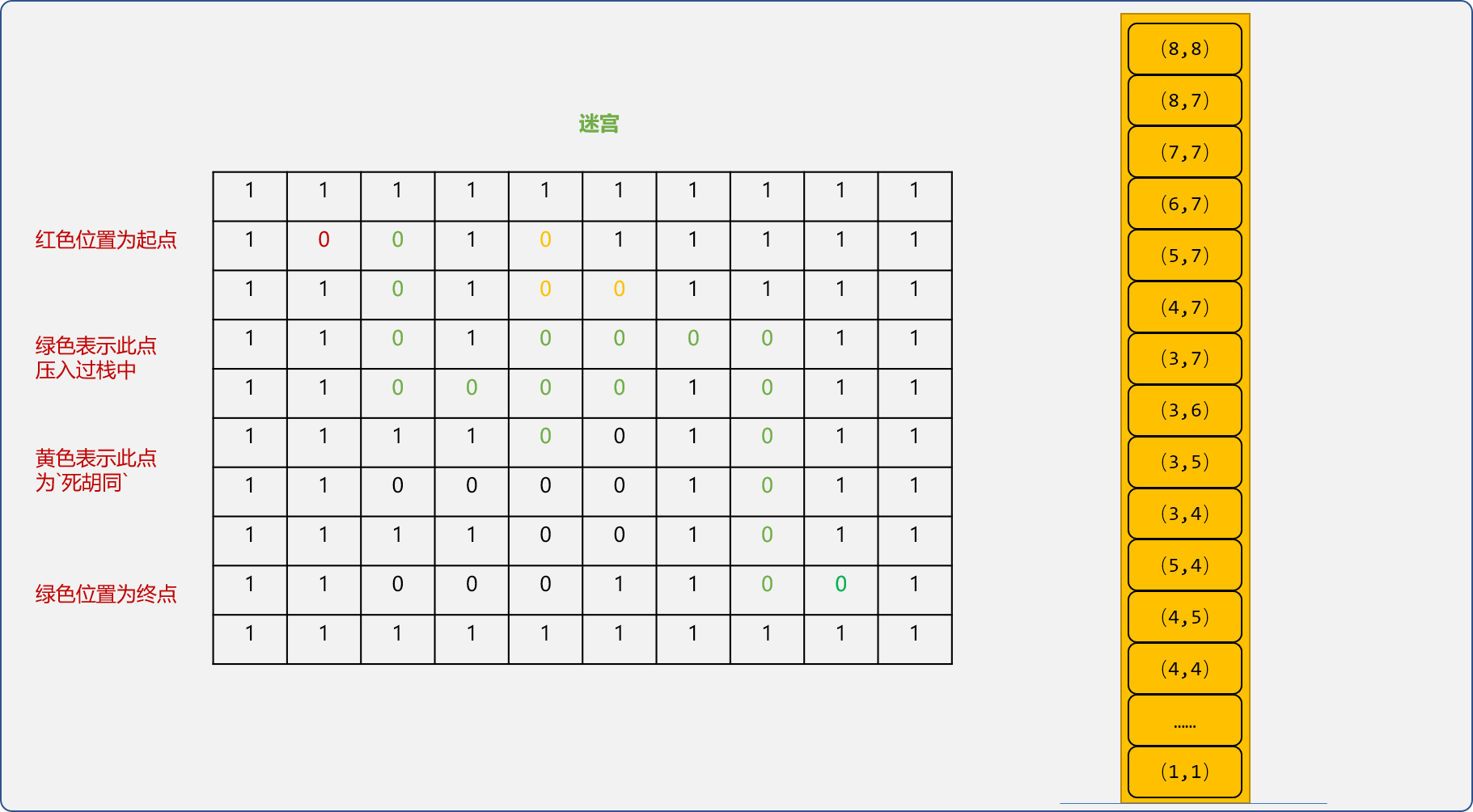
  • 重复上述的的逻辑，如下图当是添加到(4,4)单元格时栈中的内容。

5.png

  • 与(4,4)相邻的坐标分别是(4,5)、(5,4)、(4,3)、(3,4)。其中(4,3)已经访问过，则不需要再压入。栈中的坐标都是一路搜索下来可通行的位置。

6.png

  • 继续获取栈顶坐标(3,4)。随后找到与之相邻的(3，5)、(2,4)，压入栈中；再得到栈顶的(2,4)坐标，并找到与之相邻的(2,5)、(1,4)。

    Tips： 本文查找与栈顶坐标相邻的坐标是按右、下、左、上的顺序。如果顺序不同，则会导致搜索过程不一样。

7.png

  • 从栈顶得到(1,4)，因此坐标位于死胡同。于是，从栈顶把此坐标删除。可得到一个结论，不是所有进入栈中的坐标都有机会成为有效路径中的一份子。本文称行之此处不通的坐标为死胡同坐标，也做相应的标记。也就是说，当坐标为死胡同坐标时，则从栈顶删除。

8.png

  • 栈中的(2，5)、(2,4)为死胡同坐标，删除。

9.png

  • 从(3,5)坐标开始，可以一路走到终点。把栈中的坐标全部输出便得到起点到终点的有效路径。

10.png

这里有一个问题要思考，栈中的值真的全是有效路径上的坐标？

其实不然，也许有些坐标进入栈中，只为备用。如到(4,4)位置时，有 3 个可行方向(4,5)、(5,4)、(3,4)。因(3，4)这个方向可行，最终(4,5)、(5,4)备用点没用上。所以，这些坐标也需要标记一下，本文称为备用坐标。

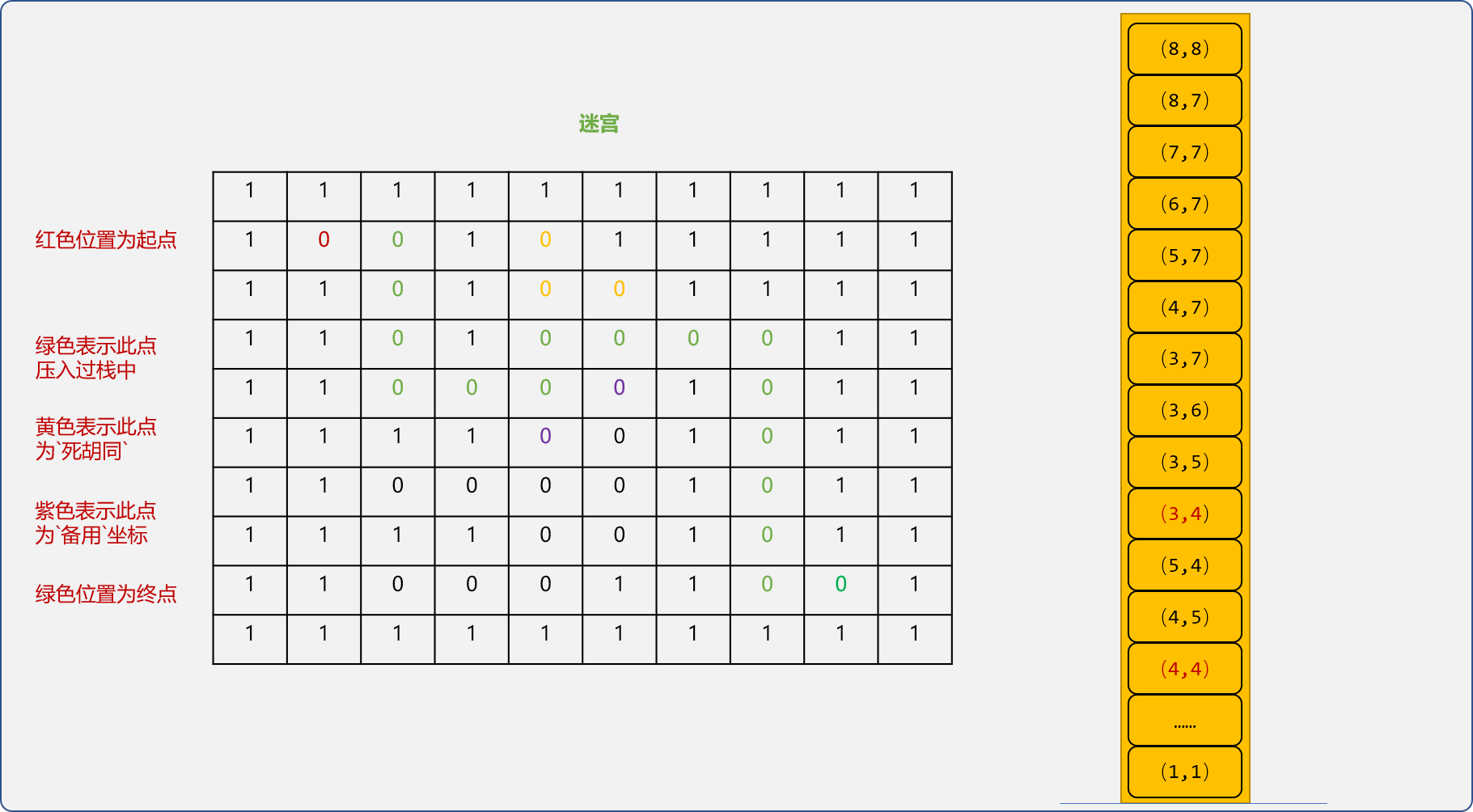
11.png

对坐标进行不同颜色标记后，上图中的绿色坐标为最终有效路径。

2.3.2 编码实现

/*
* 非递归实现路径的查找
* 只保证查找到路径
* 需要借助栈
*/
void Maze::searchPathByStack(Position start,Position end) {
	//把起始点压入栈
	Maze::mazeStack.push(start);
	//置 0,表示已经访问过
	Maze::maze[start.x][start.y]=0;
	Position top;
	Position tmpPos;
	while(1) {
		//得到栈顶的元素
		top=Maze::mazeStack.top();
		// -2 表示此坐标是路径中的一部分
		Maze::maze[top.x ][top.y ]=-2;
		if(top==end) {
			return;
		}
		bool isConnection=false;
		//检查栈顶元素的周边点
		for(int i=0; i<4; i++) {
			tmpPos= { top.x+dirs[i].xOffset,top.y+dirs[i].yOffset  };
			//检查是否可通，-1 表示可通
			if( Maze::maze[tmpPos.x ][tmpPos.y ]==-1 ) {
				isConnection=true;
				//压入栈
				Maze::mazeStack.push(tmpPos);
				//经访问过
				Maze::maze[tmpPos.x][tmpPos.y]=0;
			}
		}
		if(!isConnection) {
			//此点周边不能通用，从栈顶删除
			Maze::mazeStack.pop();
			//-3 表示死胡同坐标
			this->maze[top.x ][top.y ]=-3;
		}
	}
}

/*
*输出路径中的坐标
*
*/
void Maze::showPath() {
	cout<<"非递归查找到的路径："<<endl;
	stack<Position> paths;
	Position pos;
	while(!Maze::mazeStack.empty()) {
		pos=Maze::mazeStack.top();
		Maze::mazeStack.pop();
		if( this->maze[pos.x][pos.y]==-2 )
			paths.push(pos);
	}
    //正序输出
	while(!paths.empty()) {
		pos=paths.top();
		paths.pop();
		pos.desc();
	}
	cout<<endl;
}

测试：

int main(int argc, char** argv) {
	Maze maze;
	//起点位置
	Position startPos(1,1);
	//终点位置
	Position  endPos(8,8);
    //省略…… 
	//非递归搜索路径
	maze.searchPathByStack(startPos,endPos) ;
	maze.showPath();
	maze.showMap();
	return 0;
}

输出结果： 下图中的-2所示的坐标为有效路径描述。-3曾经进入过栈，但是死胡同坐标。0 表示没有用上的备用坐标。

12.png

2.4 递归实现

可以使用递归回溯，找出所有的路径。

/*
*递归查找路径
*/
bool Maze::searchPathByRecursion(Position start,Position end,int deep) {
	Maze::maze[start.x][start.y]=deep;
	//是否是死胡同坐标
	bool isConnection=false;
	Position tmpPos;
	//查找相邻坐标
	for(int i=0; i<4; i++ ) {
		//相邻坐标
		tmpPos= { start.x+dirs[i].xOffset,start.y+dirs[i].yOffset };
		if( Maze::maze[tmpPos.x][tmpPos.y]==-1  ) {
			//可访问
			isConnection=true;
			Maze::maze[tmpPos.x][tmpPos.y]=deep;
			if(tmpPos==end ) {
				Maze::totalCount++;
				cout<<"第"<<Maze::totalCount<<"种"<<endl;
				//输出
				Maze::showMap();
			} else {
				//递归,如果相邻坐标是死胡同，则当前坐标也是
				isConnection=Maze::searchPathByRecursion(tmpPos,end,deep+1);
			}
			//回溯时恢复状态
			//Maze::maze[tmpPos.x][tmpPos.y]=-1;
		}
	}
	if(!isConnection)
		//死胡同坐标，回溯不用判断是否死胡同
		Maze::maze[start.x][start.y]=-3;
	return isConnection;
}

测试代码：

int main(int argc, char** argv) {
	//省略……
	//递归搜索路径
	maze.searchPathByRecursion(startPos,endPos,2) ;
	return 0;
}

注释如下代码：

//Maze::maze[tmpPos.x][tmpPos.y]=-1;

会显示一条路径。如下图所示，-3表示递归过，但是死胡同的坐标。标记为大于等于 2 的位置为可正常通行。

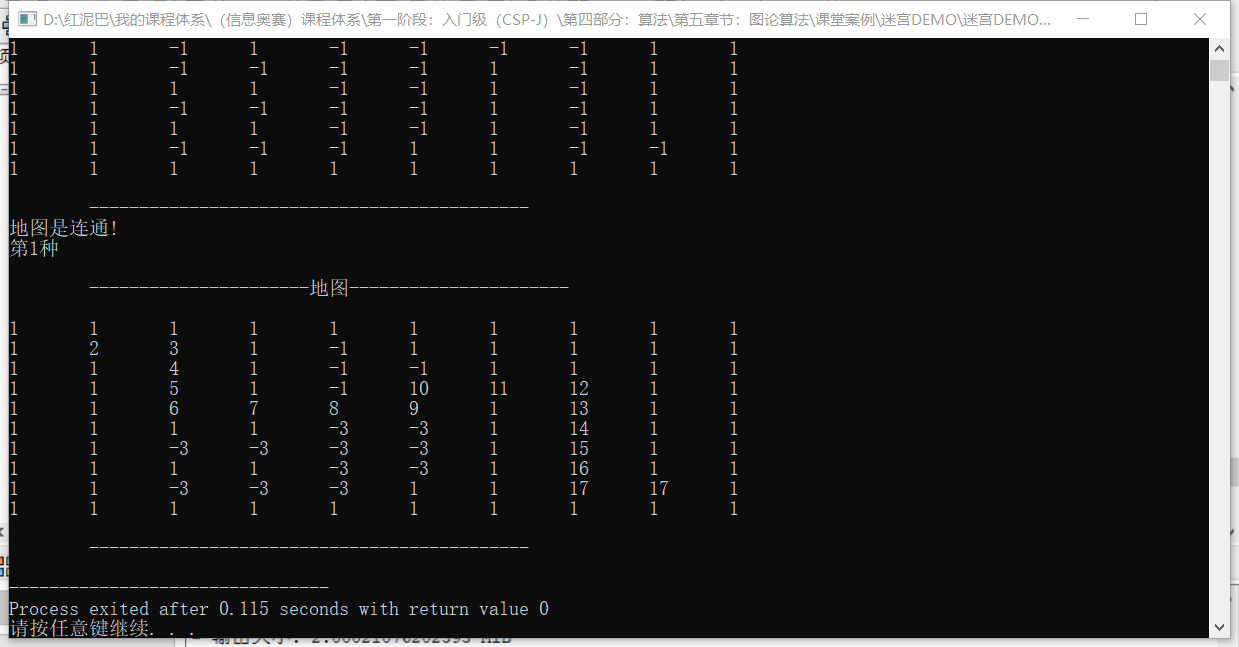
13.png

如果打开如下代码。

//回溯时恢复原来状态
Maze::maze[tmpPos.x][tmpPos.y]=-1;

显示所有路径，回溯不用判断死胡同坐标，回溯时会自动恢复原来的状态。

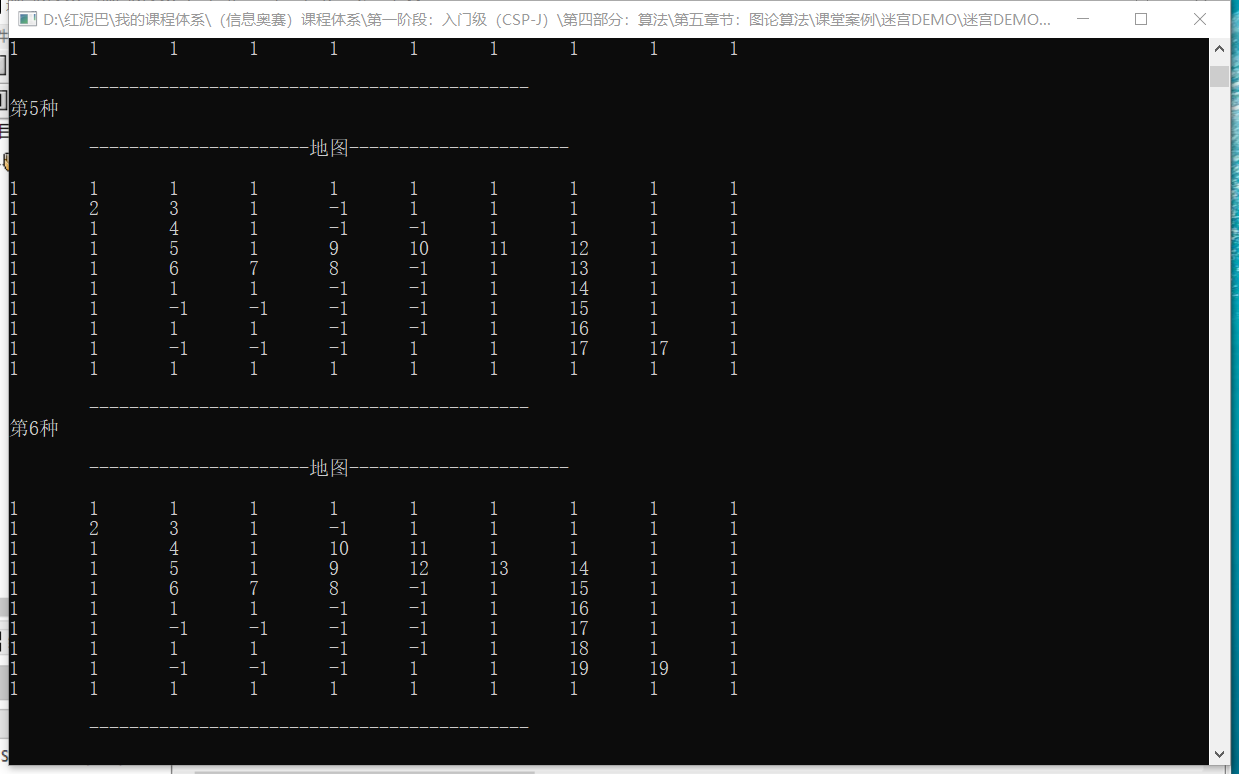
14.png

2.4 广度搜索

在家拖地时，如果从当前位置向前拖，然后再折回，这和深度优先搜索方式一样。另一种是从左向右方式，逐渐向远处外延，这和广度搜索一样。

15.png

广度优先类似于一石激起千层浪，一层层向外推动。

/*
*广度搜索
*/
void Maze::searchPathByQueue(Position start,Position end) {
    //所有路径
	vector<vector<Position>>  paths;
	//把起始点放入队列
	Maze::mazeQueue.push(start);
	vector<Position> path;
	path.push_back(start);
	paths.push_back(path);
	Position pos;
	bool isConnection;
	Position tmpPos;
	while(true ) {
		//从队列中得到队头数据
		pos=Maze::mazeQueue.front();
		Maze::mazeQueue.pop();
		for(int i=0; i<paths.size(); i++) {
			//得到所有路径
			path=paths[i];
			Position lastPos=path.back();
			for(int j=0; j<4; j++) {
				Position tmp= {lastPos.x+dirs[j].xOffset,lastPos.y+dirs[j].yOffset };
				if(tmp==pos) {
					path.push_back(pos);
					paths.push_back(path);
					break;
				}
			}
		}
		//到达终点
		if(pos==end) {
			for(int i=0; i<paths.size(); i++) {
				if( paths[i].back()==end ) {
					for(int j=0; j<paths[i].size(); j++) {
						Maze::maze[ paths[i][j].x ][paths[i][j].y]=-2;
						paths[i][j].desc();
					}
					break;
				}
			}
			return;
		}
		//查找相邻的坐标
		for(int i=0; i<4; i++) {
			tmpPos= { pos.x+dirs[i].xOffset,pos.y+dirs[i].yOffset };
			if( Maze::maze[tmpPos.x][tmpPos.y]==-1 ) {
				//可通加入队列
				Maze::mazeQueue.push(tmpPos);
				Maze::maze[tmpPos.x][tmpPos.y]=0;
			}
		}

	}
}

输出结果： 迷宫中的广度优先搜索相当于在无向图中查找路径，可以找到任何 2 个可通行位置的最短路径。这里只显示起点到终点的最短路径，如下-2所标记的位置连接起来的路径。

16.png

3. 总结

迷宫本质是矩阵，在解决迷宫问题时，可以考虑运用矩阵相关的操作理论。另，树、图的关系也常用矩阵描述，迷宫问题也可以当成树、图论算法中的子问题。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/142500.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CDH6.3.2整合DolphinScheduler3.0.0

CDH6.3.2整合DolphinScheduler3.0.0

注意事项zookeeper版本兼容要查看dolphinscheduler的libs目录下zookeeper的jar包CDH6.3.2DolphinScheduler3.0.0前置条件默认CDH以正确安装并启动至少官方要求的基础环境以正确安装并配置,点击跳转使用mysql需要驱动包 mysql-connector-java-8.0.16.jar,同时所有服务的libs里面…
阅读更多...
电力系统电价与温度模型（Matlab代码实现）

电力系统电价与温度模型（Matlab代码实现）

目录 1 数学模型 2 运行结果 3 Matlab代码实现 1 数学模型 用于模拟电价的模型是一个简化形式的混合模型&#xff0c;如下图1所示。其根本驱动因素是天然气价格和气温。该模型在内部捕获了驱动因素与电价的关系之间的关系&#xff0c;以及与一天中的时间、一周中的哪一天和…
阅读更多...
日常生产用项目一整套DevOps流水线搭建-笔记一(镜像仓库的设置)

日常生产用项目一整套DevOps流水线搭建-笔记一(镜像仓库的设置)

写在前边 很多项目新手在接手开发项目的时候,由于缺乏经验,只能通过比较笨的方法去进行项目的部署和开发.这样就会非常非常的麻烦,重复的工作很多很多.我借着一个项目开发的时机,第一次实现了我原先只在想象中的流水线部署.但是由于跟正规公司的项目规模还有差距,我们的流水线…
阅读更多...
十六、状态管理——Vuex（3）

十六、状态管理——Vuex（3）

本章概要 action 分发 action在组件中分发 action组合 action 16.7 action 在定义mutation 时&#xff0c;一条重要的原则就是 mutation 必须是同步函数。换句话说&#xff0c;在 mutation() 处理器函数中&#xff0c;不能存在异步调用。例如&#xff1a; mutations:{some…
阅读更多...
关于前端的学习

关于前端的学习

最近在网上想模拟一个ai的围棋&#xff0c;然后在gitee上找了一个算法&#xff0c;想要启动一下。https://gitee.com/changjiuxiong/myGoChess?_fromgitee_search使用说明是这样的&#xff1a;使用说明npm installnpm run dev打开index.html可自定义棋盘大小: new Game(19), n…
阅读更多...
Polynomial Round 2022 (Div. 1 + Div. 2, Rated, Prizes!)（A~E）

Polynomial Round 2022 (Div. 1 + Div. 2, Rated, Prizes!)（A~E）

A. Add Plus Minus Sign给出01字符串&#xff0c;在两两之间加入或者-&#xff0c;使得最后得到的结果绝对值最小。思路&#xff1a;统计1的个数&#xff0c;若是奇数个&#xff0c;那最后绝对值一定是1&#xff0c;否则为0&#xff0c;按照最后结果添加或1即可。AC Code&#…
阅读更多...
GD32F103-初次接触

GD32F103-初次接触

前期资料 外形 原理图 参考手册 1.芯片数据手册 2.用户手册 3.固件库使用指南 固件库解析 外设缩写 一些不常见的外设缩写。 BKP 备份寄存器 DBG 调式模块 ENET 以太网控制模块Ethernet EXMC 外部存储器控制 EXTI 外部中断事件控制器 FMC 闪存控制器 GPIO/AFIO 通用…
阅读更多...
量化股票池数据怎么分析出来的？

量化股票池数据怎么分析出来的？

量化股票池数据是怎么分析出来的呢&#xff1f;说到这个需要先来了解股票量化的基本原理&#xff0c;在正常的基础上&#xff0c;不是所有的股票数据都经过一一筛选&#xff0c;而是使用一些分析工具来执行&#xff0c;就像a股自动交易接口系统需要编写相符合条件的策略来执行&…
阅读更多...
【MySQL】MySQL存储引擎，索引，锁以及调优

【MySQL】MySQL存储引擎，索引，锁以及调优

文章目录存储引擎MySQL中的索引MySQL 索引优缺点MySQL 索引类型MySQL索引的实现MySQL中的锁MySQL8.0 新特性MySQL中调优存储引擎 MySQL 5.7 支持的存储引擎有 InnoDB、MyISAM、Memory、Merge、Archive、CSV等等存储引擎。 通过show engines; 命令查看&#xff0c;如下图 图中…
阅读更多...
【目标检测】Mask R-CNN论文解读

【目标检测】Mask R-CNN论文解读

目录&#xff1a;Mask R-CNN论文解读一、Mask-RCNN流程二、Mask-RCNN结构2.1 ROI Pooling的问题2.2 ROI Align三、ROI处理架构四、损失函数一、Mask-RCNN流程 Mask R-CNN是一个实例分割&#xff08;Instance segmentation&#xff09;算法&#xff0c;通过增加不同的分支&…
阅读更多...
PTA_1_基础编程题目集

PTA_1_基础编程题目集

文章目录PTA--基础编程题目集1、简单输出整数函数接口定义&#xff1a;裁判测试程序样例&#xff1a;输入样例&#xff1a;输出样例&#xff1a;题解&#xff1a;2、多项式求和函数接口定义&#xff1a;裁判测试程序样例&#xff1a;输入样例&#xff1a;输出样例&#xff1a;题…
阅读更多...
车载以太网 - 路由激活处理机制 - 04

车载以太网 - 路由激活处理机制 - 04

在前面我们已经介绍过DoIP的路由激活，不过主要是介绍路由激活的相关的概念；今天我们主要来介绍下路由激活的处理逻辑，进一步的了解软件对路由激活的处理机制，让我们更深入的了解DoIP这块的处理逻辑，更加有助于我们的工作中开发和测试工作的进行。 首先我们简单看下…
阅读更多...
Python中的三目(元)运算符

Python中的三目(元)运算符

Python中的三目(元)运算符 官方说明 https://docs.python.org/zh-cn/3/faq/programming.html#is-there-an-equivalent-of-c-s-ternary-operator 是否提供等价于 C 语言 "?:" 三目运算符的东西&#xff1f;有的。 语法形式如下&#xff1a; [on_true] if [expre…
阅读更多...
细说——JWT攻击

细说——JWT攻击

目录介绍什么是JWTJWT有什么用为什么引入JWTJWT的组成JWT 特征识别JWT、JWS与JWE生成JWT视频介绍JWT攻击一些靶场JWT 攻击的影响是什么&#xff1f;JWT 攻击的漏洞是如何产生的&#xff1f;如何在 Burp Suite 中使用 JWT防御JWT攻击攻击工具爆破密钥工具&#xff1a;jwtcrack爆…
阅读更多...
一个普通程序员，记录自己沪漂的2022年，2023年1月5日

一个普通程序员，记录自己沪漂的2022年，2023年1月5日

或许对于每个人而言&#xff0c;2022年都是很艰难的&#xff0c;都是充满曲折的&#xff0c;仅仅以文字记录下我的2022年&#xff0c;我的沪漂生活。 今天是2023年1月5日&#xff0c;昨天的我做了一个梦&#xff0c;梦到自己捡到很多手机&#xff0c;于是做到工位的第一件事就…
阅读更多...
（5）Qt中的日期和时间

（5）Qt中的日期和时间

QDate 日期对象格式化 d - 没有前导零的日子 (1 to 31) dd - 前导为0的日子 (01 to 31) ddd - 显示(缩写) 周一、周二、周三、周四、周五、周六、周日 dddd - 显示(完整) 星期一、星期二、…
阅读更多...
微服务三个阶段

微服务三个阶段

微服务三个阶段微服务三个阶段&#xff1a;微服务1.0&#xff1a;仅使用注册发现&#xff0c;基于Spring Cloud 或 Dubbo开发。微服务2.0&#xff1a;使用熔断、限流、降级等服务治理策略&#xff0c;并配备完整微服务工具和平台。微服务3.0&#xff1a;Service Mesh将服务治理…
阅读更多...
https安全传输揭秘

https安全传输揭秘

HTTPS是什么 我们知道HTTP是明文传输的&#xff0c;恶意的中间人和窃听者通过截取用户发送的网络数据包可以拿到用户的敏感信息。尤其是涉及网上交易&#xff0c;银行转账等操作更是危害极大。 HTTPS的核心是SSL/TLS安全协议层&#xff0c;该层位于应用层和传输层之间&#x…
阅读更多...
初识异常（Java系列10）

初识异常（Java系列10）

目录 前言&#xff1a; 1.异常的概念 2.异常的分类 2.1编译时异常 2.2运行时异常 3.异常的处理 3.1如何抛出异常 3.2异常的捕获 3.2.1异常的声明 3.2.2try-catch捕获并处理 3.3异常的处理流程 4.自定义异常类 结束语&#xff1a; 前言&#xff1a; 相信在大家学…
阅读更多...
Windows常用命令整理

Windows常用命令整理

之前写了一篇关于Windows快速打开服务_陌客依天涯的博客-CSDN博客_服务快捷键 的文章&#xff0c;有表示windows还有很多常用的&#xff0c;那就整理一下&#xff0c;分享跟多点&#xff0c;希望对大家有用。 1、mstsc /*快速开启远程连接客户端*/ 2、regedit /*快速打开注册…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023