A. Add Plus Minus Sign

给出01字符串,在两两之间加入+或者-,使得最后得到的结果绝对值最小。
思路:统计1的个数,若是奇数个,那最后绝对值一定是1,否则为0,按照最后结果添加+或1即可。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int t, n;
std::string s;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n >> s;
int cnt = 0;
std::vector<char> vec;
for(int i = 0; i < n; i ++) {
if(s[i] == '1') cnt ++;
}
if(cnt & 1) cnt = 1;
else cnt = 0;
int ans = s[0] - '0';
for(int i = 1; i < n; i ++) {
if(ans < cnt) {
ans += (s[i] - '0');
vec.push_back('+');
}
else {
ans -= (s[i] - '0');
vec.push_back('-');
}
}
for(auto u : vec) {
std::cout << u;
}
std::cout << '\n';
}
return 0;
}B. Coloring

一共有n个格子,m种颜色,每种颜色需要涂满a[i]个格子,连续k个格子中每种颜色不能出现两次及以上,问是否存在满足条件上色的方案。
思路:我们可以将n个格子分成n/k段,显然,需要最多的颜色小于等于n/k显然是可以的;若是存在需要颜色是n/k+1的情况也是可以的,但是最后零出来的一段中,满足该情况的颜色不能多余n%k个,否则定然不满足情况;显然,若存在某种颜色是大于n/k+1的,那一定不可以。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
#define int long long
const int N = 1e5 + 5;
int t, n, m, k;
int a[N];
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n >> m >> k;
std::map<int, int> mp;
int max = 0;
for(int i = 1; i <= m; i ++) {
std::cin >> a[i];
max = std::max(max, a[i]);
mp[a[i]] ++;
}
if(max <= n / k)
std::cout << "YES" << '\n';
else if(max == n / k + 1 && mp[max] <= n % k)
std::cout << "YES" << '\n';
else
std::cout << "NO" << '\n';
}
return 0;
}os:一开始忘记了满足个数为n/k+1的颜色种类完全可以不是一种,结果WA10了
C. Ice and Fire

给出一行n-1个字符,0代表数字小者胜,1代表数字大者胜,有1~n个数,对于每一局,有2~n个人,求每次有多少人可以胜出。
思路:从字符串入手,我们可以分析连续每局胜负之间的关系:
(1)11型,即相连两局为11,这样后一局加入的人可以将前面胜出的一人取代,所以胜者数量不变;
(2)00型,即相连两局为00,这样后一局加入的人会被前一局胜出的一人打败,所以胜者数量不变;
(3)01型,即相连两局为01,这样后一局加入的人会淘汰掉上一局的胜者,但是他也可以在前面连续的0中被前面的数字淘汰,这样后一局的胜者完全可以是前面连续0的个数;
(4)10型,即相连两局为10,这样后一局加入的人会被前一局胜出的一人打败,但是他可以在前面淘汰掉前面的人,使得放到该局与他对战的人胜出,与01型相同,则后一局的胜者可以是前面相连1的个数。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 2e5 + 5;
int t, n;
std::string s;
int f[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n >> s;
f[0] = 1;
for(int i = 0; i < n - 1;) {
int j = i + 1;
int idx = 1;
while(j < n - 1 && s[j] == s[i]) {
idx ++;
f[j] = f[j - 1];
j ++;
}
if(j >= n - 1) break;
f[j] = f[j - 1] + idx;
i = j;
}
for(int i = 0; i < n - 1; i ++) {
std::cout << f[i] << " \n"[i == n - 2];
}
}
return 0;
}D. Same Count One

有n个m大小的数组,每个数组由01组成,问是否通过两行相同位置的数字交换,使得每个数组中1的数量相等,输出最少操作次数和操作方法,否则输出-1。
思路:很显然,不能满足条件的情况是1的个数不能整除n。其他的情况,直接模拟即可。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 2e5 + 5;
int t, n, m;
std::string s;
struct node {
int x, y, z;
};
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n >> m;
int a[n + 1][m + 1];
memset(a, 0, sizeof(a));
int cnt = 0;
for(int i = 1; i <= n; i ++) {
for(int j = 1; j <= m; j ++) {
std::cin >> a[i][j];
a[i][0] += a[i][j];
if(a[i][j])
cnt ++;
}
}
if(cnt % n) {
std::cout << -1 << '\n';
continue;
}
std::vector<int> b, c;
std::vector<node> ans;
cnt = cnt / n;
for(int j = 1; j <= m; j ++) {
b.clear(), c.clear();
for(int i = 1; i <= n; i ++) {
if(a[i][0] < cnt && !a[i][j])
b.push_back(i);
if(a[i][0] > cnt && a[i][j])
c.push_back(i);
}
for(int i = 0; i < std::min(b.size(), c.size()); i ++) {
a[b[i]][0] ++, a[c[i]][0] --;
ans.push_back({b[i], c[i], j});
}
}
std::cout << ans.size() << '\n';
for(auto u : ans) {
std::cout << u.x << ' ' << u.y << ' ' << u.z << '\n';
}
}
return 0;
}E. Two Chess Pieces

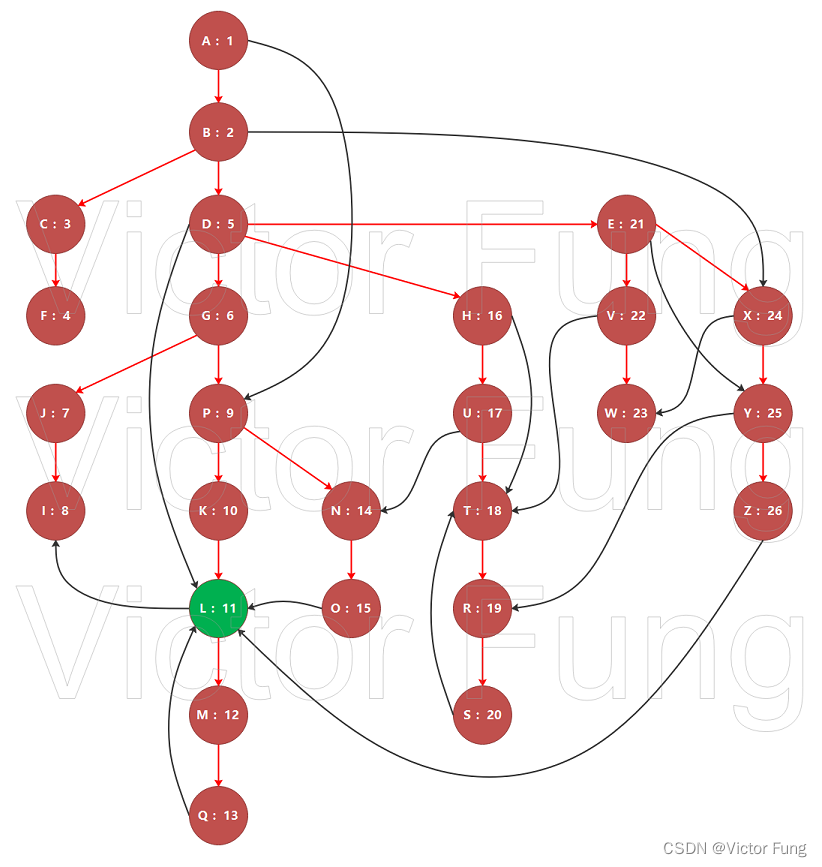
给出一棵树,在1节点处有两个棋子,两个棋子每次移动可以移动到相邻的节点上,两个棋子之间的距离不能大于d,给出两个棋子需要移动至的位置,问若两棋子分别到达各自需要移动到的位置,并返回1节点,最少需要移动多少次。
思路:因为要从1处移动并最后回到1处,所以可知最短路径是路径*2。对于棋子的必经节点有两种情况,一种是要访问节点的祖先。另一种是被另外一个棋子限制所必须访问的节点。一个节点是必经的节点,当且仅当节点子树中有要访问的节点或者子树中有另一个棋子要访问的节点距离这个节点的距离大于等于d。所以可以先DFS求出每个节点距离d的祖先,存于a数组中。接着,再用两次DFS就能分别求出两个棋子必经节点了,即两遍DFS处理f数组,即每个节点是否为必经节点。
除了必经节点,最优情况,我们不必再访问其他节点了。我们可以让其中棋子一个按最优的顺序遍历必经点,而另一个棋子就可以在当第一个棋子访问u的时候,顺便访问u子树中被限制的节点。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 2e5 + 5;
int n, d;
std::vector<int> vec[N], path;
int a[N], f[2][N];
void DFS(int u, int fa, const int d) {
path.push_back(u);
a[u] = 1;
if(path.size() > d)
a[u] = path[path.size() - 1 - d];
for(auto v : vec[u]) {
if(v == fa)
continue;
DFS(v, u, d);
}
path.pop_back();
}
void DFS1(int u, int fa, int chess) {
bool flag = false;
for(auto v : vec[u]) {
if(v == fa)
continue;
DFS1(v, u, chess);
flag |= f[chess][v];
}
f[chess][u] |= flag;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n >> d;
for(int i = 1; i < n; i ++) {
int u, v;
std::cin >> u >> v;
vec[u].push_back(v);
vec[v].push_back(u);
}
DFS(1, 0, d);
for(int i = 0; i <= 1; i ++) {
int m;
std::cin >> m;
for(int j = 1; j <= m; j ++) {
int x;
std::cin >> x;
f[i][x] = f[i ^ 1][a[x]] = 1;
}
}
DFS1(1, 0, 0);
DFS1(1, 0, 1);
int res = 0;
for(int i = 0; i <= 1; i ++) {
res += std::accumulate(&f[i][2], &f[i][n + 1], 0);
}
std::cout << res * 2 << '\n';
return 0;
}