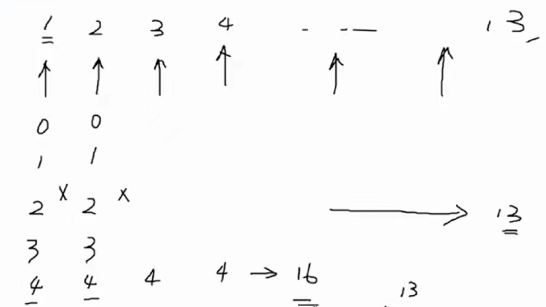给定一个整数 n
和 m
个不同的质数 p1,p2,…,pm
。

请你求出 1∼n
中能被 p1,p2,…,pm
中的至少一个数整除的整数有多少个。

输入格式
第一行包含整数 n
和 m
。

第二行包含 m
个质数。

输出格式
输出一个整数，表示满足条件的整数的个数。

数据范围
1≤m≤16
,
1≤n,pi≤109
输入样例：
10 2
2 3
输出样例：
7
题目最好使用容斥原理。

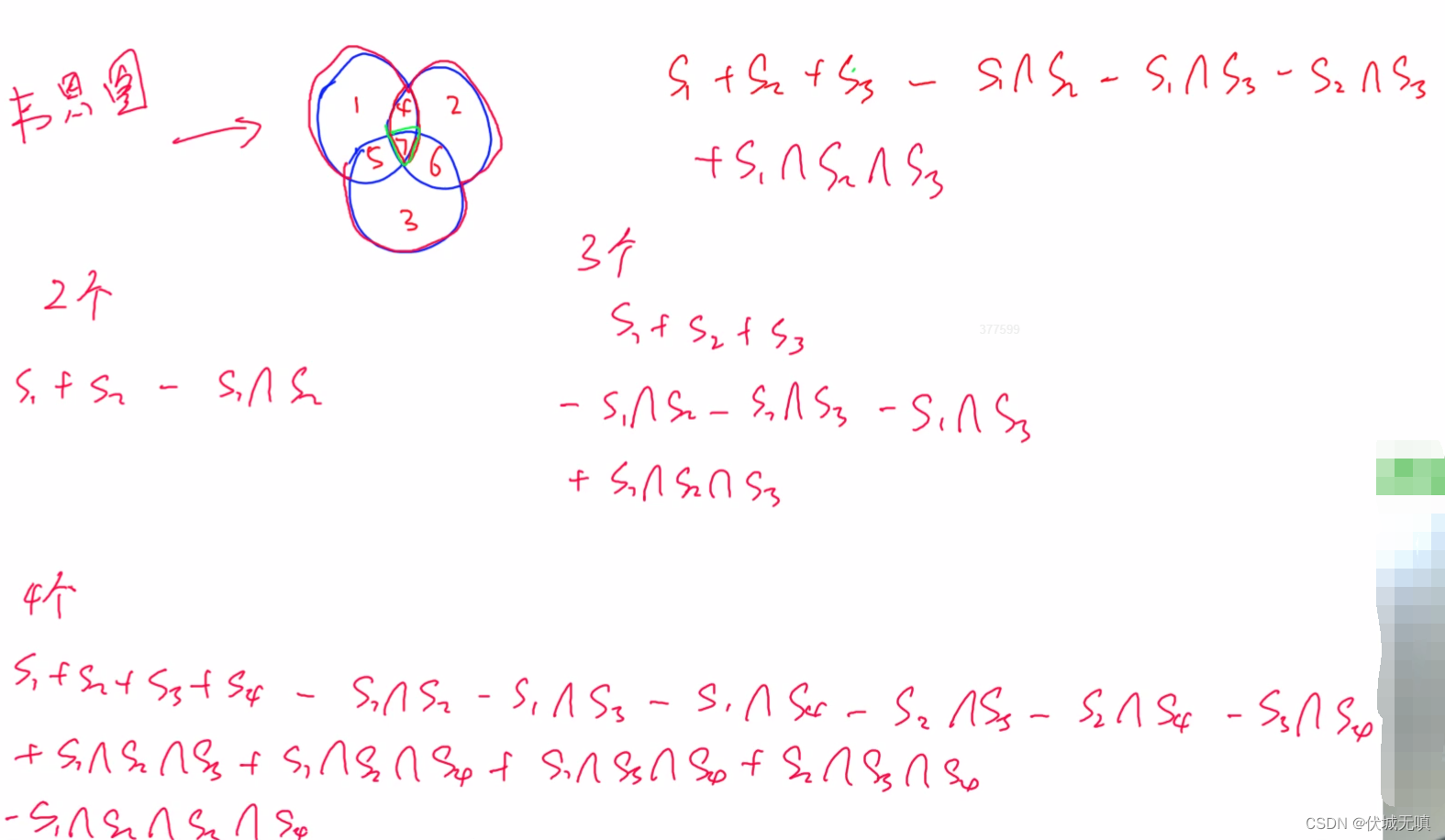
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;
const int N = 20;

int n, m;
int p[N];

int main ()
{
    cin>>n>>m;
    for(int i = 0; i < m; i ++ ) cin>>p[i];
    
    int res = 0;
    for(int i = 1; i < 1 << m; i ++ )
    {
        int t = 1, cnt = 0;
        for(int j = 0; j < m; j ++ )
        {
            if(i >> j & 1)
            {
                cnt ++;
                if((LL)t * p[j] > n)
                {
                    t = -1;
                    break;
                }
                t *= p[j];
            }
        }
        if(t != -1)
        {
            if(cnt % 2) res += n / t;
            else res -= n / t;
        }
    }
    cout<<res<<endl;
    
    return 0;
}