题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
输入格式
第一行包含两个整数 N,M,表示该图共有 N 个结点和 M 条无向边。
接下来 M 行每行包含三个整数Xi,Yi,Zi,表示有一条长度为 Zi 的无向边连接结点 Xi,Yi。
输出格式
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。
输入输出样例
输入 #1
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
输出 #1
7
说明/提示
数据规模:
对于 20% 的数据,N≤5,M≤20。
对于 40% 的数据,N≤50,M≤2500。
对于 70% 的数据,N≤500,M≤104。
对于 100% 的数据:1≤N≤5000,1≤M≤2×10^5,1≤Zi≤10^4。
样例解释:
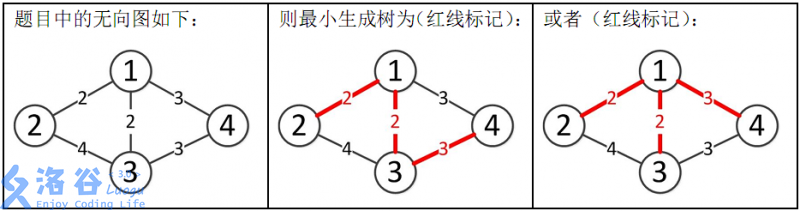
所以最小生成树的总边权为 2+2+3=7。
本题考察最小身成树的构造,两种解法,普里姆(prim)算法和克鲁斯卡尔(kruskal)算法
两种算法的时间复杂度分别为O(n^2)和O(e*loge),n为顶点数,e为边数,本题两种解法,题目范围可知消耗时间差不多
普里姆(prim)算法
普里姆(prim)算法的思想是任取一顶点为其起始点,选择与起始点相连的边中权值最小的一个作为生成树的边,然后在从这条边的另一个点和起始点的所有边选一条权值最小的边,重复如此,选择的边的另一个点必须是没有在树中。
思路如上,普里姆一般用邻接矩阵,判断是否为连通图只需要dfs遍历一次,若是连通图,dfs遍历一次就能将所有点标记
#include<stdio.h>
int a[5001][5001];
void vie(int x)//无向图初始化
{
for (int i = 1; i <= x; i++)
for (int j = i; j <= x; j++)
{
if (i == j)
a[i][j] = 0;
else
{
a[j][i] = 1e9;
a[i][j] = 1e9;
}
}
}
int book[5001], n;
void dfs(int x)//dfs遍历图
{
book[x] = 1;
for (int i = 1; i <= n; i++)
if (a[x][i] < 1e9 && book[i] == 0)
dfs(i);
}
int main()
{
int m, i, j, x, y, z;
scanf("%d %d", &n, &m);
vie(n);//初始化邻接矩阵
for (i = 1; i <= m; i++)//输入边
{
scanf("%d %d %d", &x, &y, &z);
if(a[x][y]>z)
{
a[x][y] = z;
a[y][x] = z;
}
}
dfs(1);//判断是否为连通图
for (i = 1; i <= n; i++)
{
if (book[i] == 0)//存在没有遍历到的点,不是连通图
{
printf("orz");
return 0;
}
}
int dis[5001];//松弛数组
for (i = 1; i <= n; i++)//初始化以1作为起始点
dis[i] = a[1][i];
int sum = 0;//统计最小各个长度和
for (i = 2; i <= n; i++)//n个结点,需要构造n-1条边
{
int min = 1e9, k = 0;
for (j = 2; j <= n; j++)//寻找最小权值的边,第1个点已经确定不用判断
{
if (dis[j] != 0 && min > dis[j])
{
min = dis[j]; k = j;
}
}
sum += min;//加上该边的权值
dis[k] = 0;
for (j = 1; j <= n; j++)
if (dis[j] > a[k][j])
dis[j] = a[k][j];
}
printf("%d", sum);
return 0;
}克鲁斯卡尔(kruskal)算法
克鲁斯卡尔(kruskal)算法的思想是每次选择权值最小的边,前提是这条边的两个顶点之间没有 联系,每次选权值最小的边好办,对边进行排序,判断两个点是否有联系,可以用并查集,对于边提前用边集数组储存,根据权值进行排序,选n-1条边结束
这题用 克鲁斯卡尔(kruskal)算法解决对于这题判断图是否是连通图只需要判断并查集数组里面有几个老大,若是超过1则不是连通图。
#include<stdio.h>
struct nb {
int l, r, data;
}a[200001];//结构体数组储存每条边的信息
int n, m, ss[5001];//ss为并查集数组
void kp(int x, int y)//快速排序
{
if (x >= y)return;
int left = x, right = y;
struct nb temp = a[x], t;
while (left < right)
{
while (a[right].data >= temp.data && left < right)
right--;
while (a[left].data <= temp.data && left < right)
left++;
if (left < right)
{
t = a[left]; a[left] = a[right]; a[right] = t;
}
}
a[x] = a[left]; a[left] = temp;
kp(x, left - 1);
kp(left + 1, y);
}
int find(int x)//寻找x点的老大
{
if (ss[x] == 0)
return x;
else
{
ss[x] = find(ss[x]);//路径压缩
return ss[x];
}
}
int bing(int x, int y)//判断x,y的老大是否为同一个,是的话返回0
{
int t1 = find(x);//x的老大
int t2 = find(y);//y的老大
if (t1 != t2)
{
ss[t1] = t2;
return 1;
}
return 0;
}
int main()
{
int i, j;
scanf("%d %d", &n, &m);
for (i = 1; i <= m; i++)
scanf("%d %d %d", &a[i].l, &a[i].r, &a[i].data);//输入边
kp(1, m);//升序排序
int sum = 0, count = 0;
for (i = 1; i <= m; i++)
{
if (bing(a[i].l, a[i].r))//如果边的两点没有联系
{
sum += a[i].data;//统计边权值的和
count++;//最小生成树边的数量加1
}
if (count == n - 1)//选到n-1条边后直接结束
break;
}
int kk = 0;
for (i = 1; i <= n; i++)//寻找老大数量
if (ss[i] == 0)
kk++;
if (kk > 1)//超过1不是连通图,不能生成树
printf("orz");
else
printf("%d", sum);
return 0;
}