Problem: 295. 数据流的中位数

思路

👨‍🏫 参考

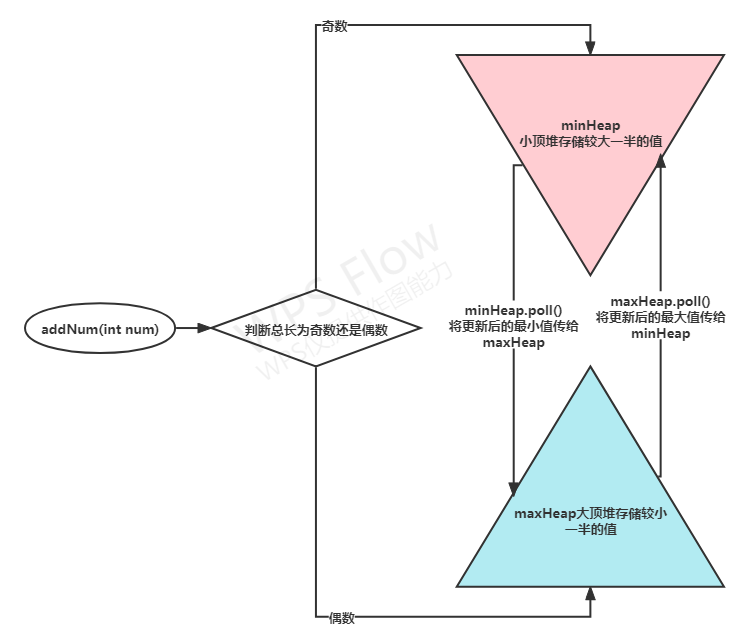
• 大根堆维护较小值（堆顶即中位数），小根堆维护较大值（堆顶可能是中位数之一）
• 维护小堆长度较长，大堆较短；
• 添加元素时需保证大的加到值大的一半，小的加到值小的一半；所以需要先排序后仔加入。
  

复杂度

时间复杂度:

💖 Code

class MedianFinder {

	PriorityQueue<Integer> maxHeap;
	PriorityQueue<Integer> minHeap;

	public MedianFinder()
	{
		maxHeap = new PriorityQueue<>((x, y) -> (y - x));
		minHeap = new PriorityQueue<>();
	}

	public void addNum(int num)
	{
		if (maxHeap.size() != minHeap.size())
		{
//			 长度为奇数时先放入小顶堆,重新排序后在插入到大顶堆
			minHeap.add(num);
			maxHeap.add(minHeap.poll());
		} else
		{
//			  长度为偶数时先放入大顶堆,重新排序后在插入到小顶堆
			maxHeap.add(num);
			minHeap.add(maxHeap.poll());
		}
	}

	public double findMedian()
	{
		if (minHeap.size() != maxHeap.size())
			return minHeap.peek();
		else
			return (minHeap.peek() + maxHeap.peek()) / 2.0;
	}
}