深度学习与神经网络pytorch版 2.3 线性代数

目录

深度学习与神经网络pytorch版 2.3 线性代数

1. 简介

2. 线性代数

2.3.1 标量

​编辑2.3.2 向量

2.3.3 矩阵

2.3.4 张量及其性质

2.3.5 降维

2.3.6 非降维求和

2.3.7 点积

2.3.8 矩阵-向量积

2.3.9 矩阵-矩阵乘法

2.3.10 范数

3. 小结

1. 简介

  深度学习与线性代数之间有着密切的联系。线性代数是深度学习算法中用于表达和处理数据的数学工具之一，尤其是在构建神经网络和处理多维数据时。

线性代数中的基本概念包括向量、矩阵和线性变换等，这些概念在深度学习中有着广泛的应用。例如，在神经网络的训练过程中，权重和偏差可以看作是矩阵和向量，它们通过线性变换来改变输入数据的特征，从而实现分类或回归等任务。

此外，线性代数中的范数也是深度学习中常用的概念。范数可以用来衡量向量的大小，对于限制模型复杂度和提升模型的泛化能力具有重要作用。在深度学习中，范数通常用于正则化、优化算法等。

最后，特征值分解是线性代数中的另一个重要概念，它在深度学习中用于将矩阵分解成一组特征向量和特征值。特征值分解可以帮助我们了解数据的内在结构和关系，例如在降维、数据可视化等方面有着广泛的应用。

综上所述，线性代数在深度学习中扮演着重要的角色，它为深度学习提供了数学基础和工具，使得我们能够更好地理解和处理复杂的数据结构和模式。

2. 线性代数

2.3.1 标量

# 2.3.1 标量
# 导入PyTorch库。PyTorch是一个开源的深度学习库，提供了张量计算等功能。  
import torch
# 打印字符串'2.3.1 标量'到控制台。  
print('2.3.1 标量')
# 使用torch.tensor()函数创建一个标量张量x1，其值为4.0。  
x1 = torch.tensor(4.0)
# 使用torch.tensor()函数创建另一个标量张量y1，其值为3.0。  
y1 = torch.tensor(3.0)
# 打印x1和y1的和。由于x1和y1都是标量，所以直接相加即可。  
print(x1 + y1)
# 打印x1和y1的乘积。  
print(x1 * y1)
# 打印x1除以y1的结果。 
print(x1 / y1)
# 打印x1的y1次幂。 
print(x1 ** y1)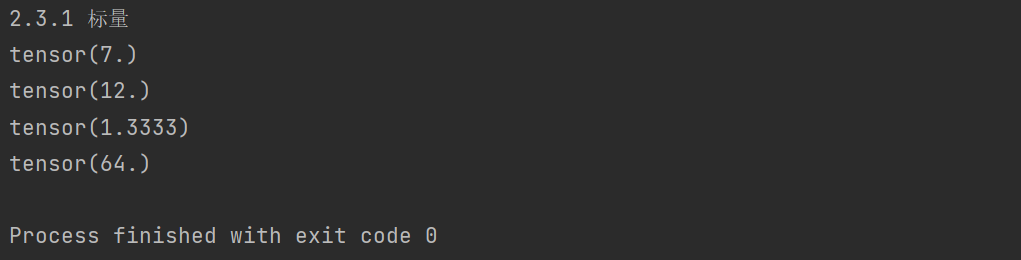

2.3.2 向量

# 2.3.2 向量
import torch
print('2.3.2 向量')
x2 = torch.arange(6)
print(x2)
print(x2[4]) # 可以通过x[i]来引用第个i个元素(从0开始)
print(len(x2)) # 通过len()函数来访问长度
print(x2.shape) # 通过.shape属性访问向量的长度

2.3.3 矩阵

# 2.3.3 矩阵
import torch
print('2.3.3 矩阵')
A = torch.arange(20).reshape(5,4)
print(A)
W = A.T # 交换矩阵的行和列时，结果称为矩阵的转置（transpose）
print(W)
B = torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
print(B)
E = B == B.T # 对称矩阵（symmetric matrix）
print(E)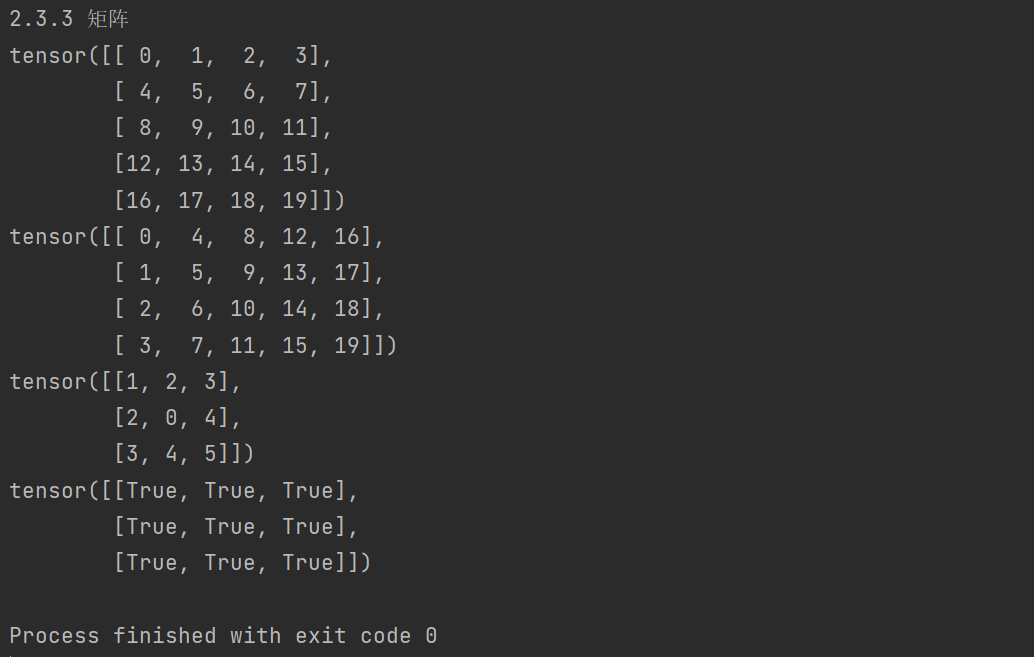

2.3.4 张量及其性质

# 2.3.4 张量及其性质
import torch
print('2.3.4 张量')
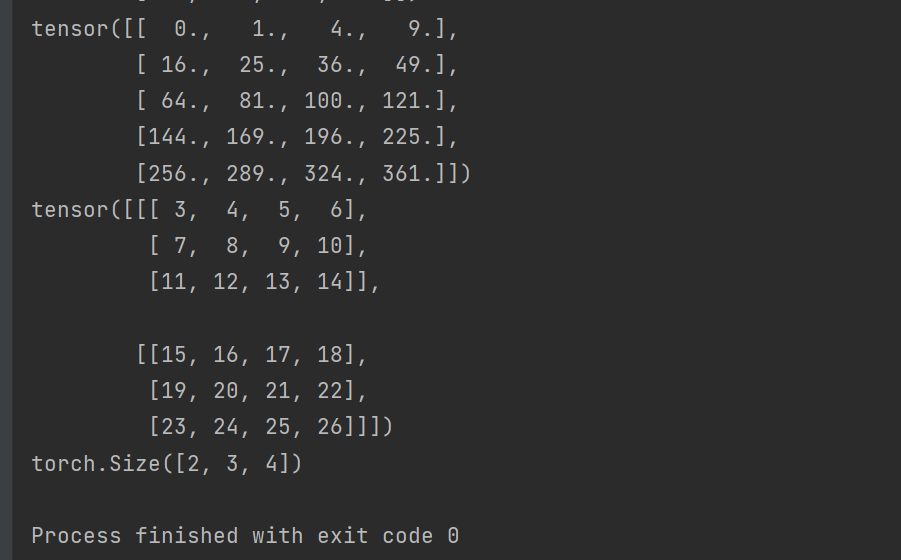
X3 = torch.arange(24).reshape(2,3,4)
print(X3)
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
B = A.clone() # 重新分配内存，将A复制给B
print(A)
print(A + B)
print(A * B)
# 将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘
a = 3
X4 = torch.arange(24).reshape(2,3,4)
print(a + X4)
print((a * X4).shape)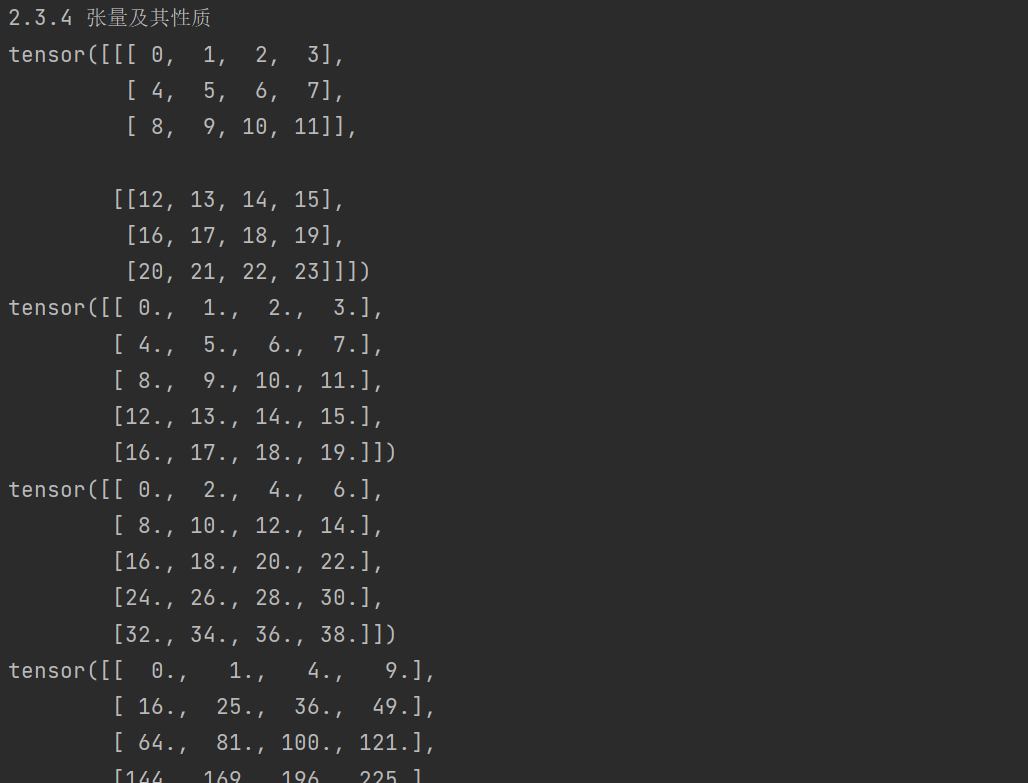

2.3.5 降维

# 2.3.5 降维

import torch 
print('2.3.5 降维')
# 创建一个从0到3的浮点数张量，总共有4个元素。  
x = torch.arange(4, dtype=torch.float32)
print(x)  # 输出: tensor([0., 1., 2., 3.])  
print(x.sum())  # 输出: 6.0，求和结果为1+2+3=6  

# 创建一个20元素的浮点数张量，并将其重新塑形为一个5x4的二维张量。  
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
  

print(A.shape)  # 输出: tensor([5, 4])，表示张量A有5行和4列。  
print(A.sum())  # 输出: 120.0，求和结果为0+1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19=120  
# 对A的每一列求和，结果为一个包含5个元素的张量。  
A_sum_axis0 = A.sum(axis=0)
print(A_sum_axis0)  # 输出: tensor([30., 35., 40., 45., 50.])  
print(A_sum_axis0.shape)  # 输出: tensor([5])，表示每个元素都是一个独立的张量。  

# 对A的每一行求和，结果为一个包含4个元素的张量。  
A_sum_axis1 = A.sum(axis=1)
print(A_sum_axis1)  # 输出: tensor([ 6.,  6.,  6.,  6.,  6.])  
print(A_sum_axis1.shape)  # 输出: tensor([5])，表示每个元素都是一个独立的张量。  

# 同时对A的行和列求和。结果为一个单一的数值。  
print(A.sum(axis=[0, 1]))  # 输出: 600.0，求和结果为(0+4+8+12+16)+(1+5+9+13+17)+(2+6+10+14+18)+(3+7+11+15+19)=600  
print(A.mean())  # 输出: tensor(6.)，计算所有元素的平均值。  
print(A.sum() / A.numel())  # 输出: tensor(6.)，计算所有元素的平均值。通过总和除以元素总数得到。  
print(A.mean(axis=0),
      A.sum(axis=0) / A.shape[0])  # 输出: tensor([6., 7., 8., 9.]) 和 tensor([7., 7., 7., 7.])。分别计算每列和每行的平均值。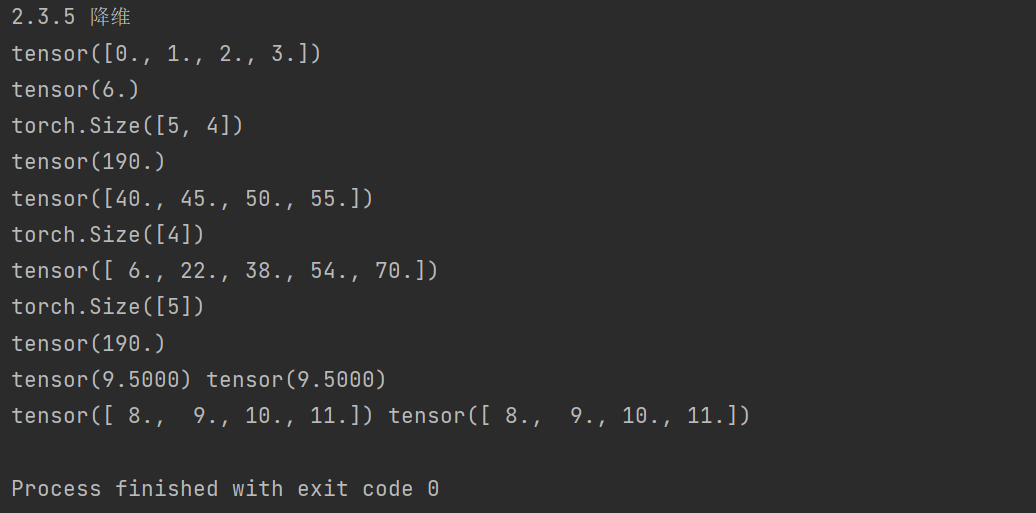

2.3.6 非降维求和

# 2.3.6 非降维求和
print('2.3.6 非降维求和')
import torch
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
sum_A = A.sum(axis=1, keepdims=True)
print(sum_A)
print(A / sum_A) #由于sum_A在对每行进行求和后仍保持两个轴，我们可以通过广播将A除以sum_A。
print(A.cumsum(axis=0))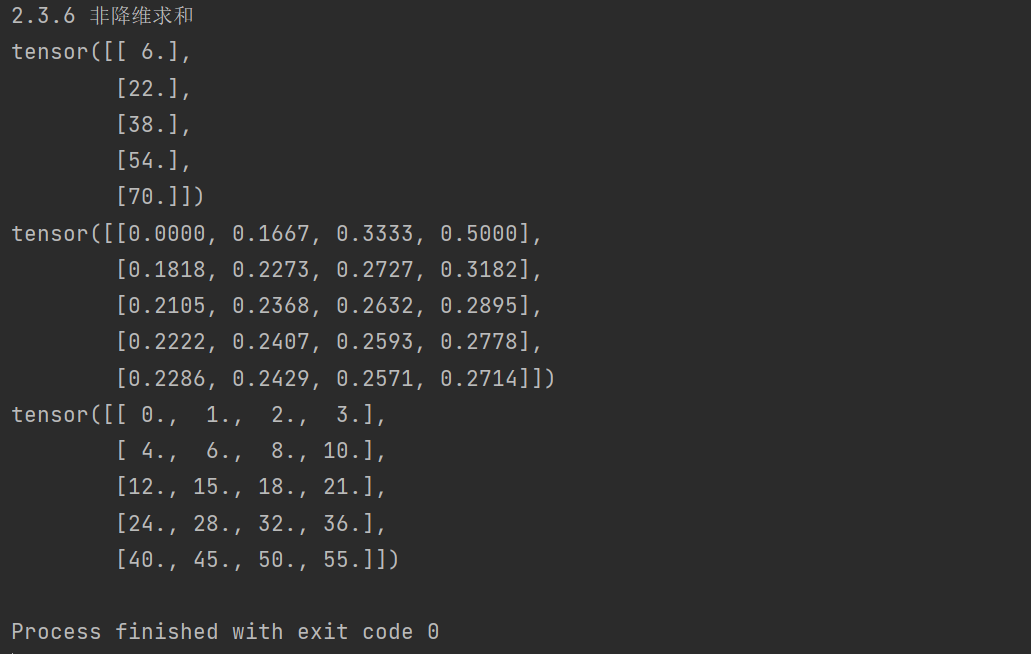

2.3.7 点积

# 2.3.7 点积
import torch
print('2.3.7 点积')
x = torch.arange(4, dtype=torch.float32)

y = torch.ones(4, dtype = torch.float32)
print(x)
print(y)
print(torch.dot(x, y))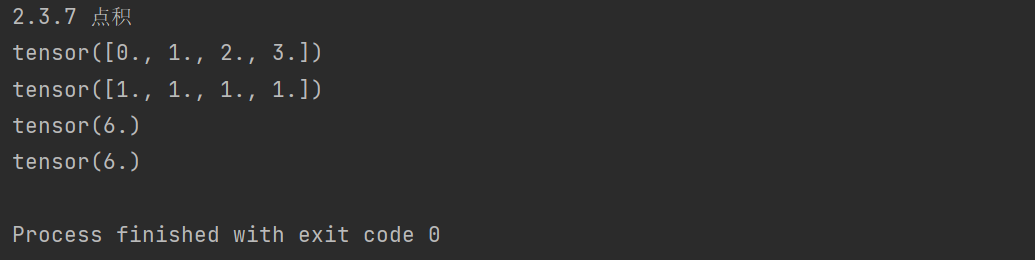

2.3.8 矩阵-向量积

# 2.3.8. 矩阵-向量积

import torch
print('2.3.8. 矩阵-向量积')
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
x = torch.arange(4, dtype=torch.float32)

print(A.shape)
print(x.shape)
print(torch.mv(A, x))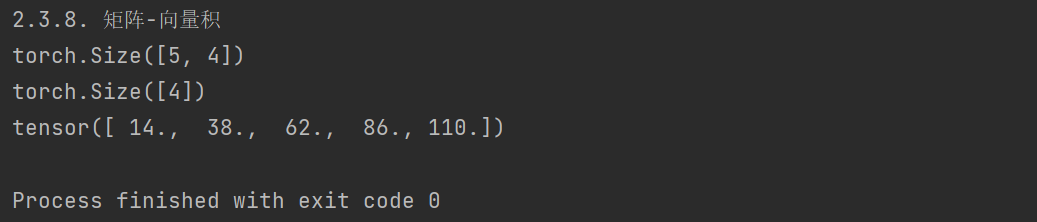

2.3.9 矩阵-矩阵乘法

# 2.3.9. 矩阵-矩阵乘法
import torch
print('2.3.9. 矩阵-矩阵乘法')
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
B = torch.ones(4, 3)
print(torch.mm(A, B))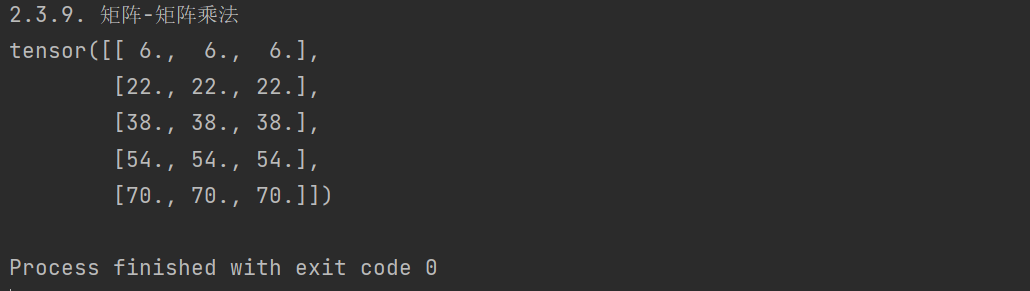

2.3.10 范数

# 2.3.10. 范数
import torch
print('2.3.10. 范数')
# 创建一个包含两个浮点数的张量u。  
u = torch.tensor([3.0, -4.0])
print(torch.norm(u))  # 输出: 5.0，计算u的范数（默认使用欧几里得范数）。  

# 计算张量u中每个元素的绝对值之和。  
print(torch.abs(u).sum())  # 输出: 7.0，绝对值之和为3+4=7。  

# 创建一个形状为(4,9)的全1张量，并计算其范数。  
print(torch.norm(torch.ones((4, 9))))  # 输出: 9.0，计算全1张量的范数（默认使用欧几里得范数）。

3. 小结

1. 标量、向量、矩阵和张量是线性代数中的基本数学对象。

2. 向量泛化自标量，矩阵泛化自向量。

3. 标量、向量、矩阵和张量分别具有零、一、二和任意数量的轴。

4. 一个张量可以通过sum和mean沿指定的轴降低维度。

5. 两个矩阵的按元素乘法被称为他们的Hadamard积。它与矩阵乘法不同。

6. 在深度学习中，我们经常使用范数，如\(L_1\)范数、\(L_2\)范数和Frobenius范数。

7. 我们可以对标量、向量、矩阵和张量执行各种操作。