【代码随想录】刷题笔记Day56

news2024/9/22 15:25:56

前言

26回了老家参加二姨的婚礼，还逛了几圈亲戚，回来就接家教的活，想到还要刷题开组会，回家注定是没法怎么休息啦，可恶

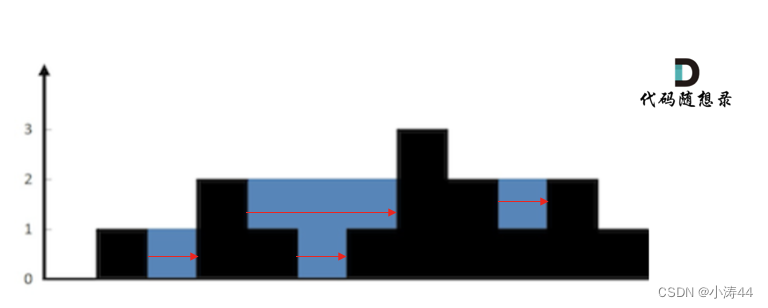
42. 接雨水 - 力扣（LeetCode）

暴力解法（双指针优化）

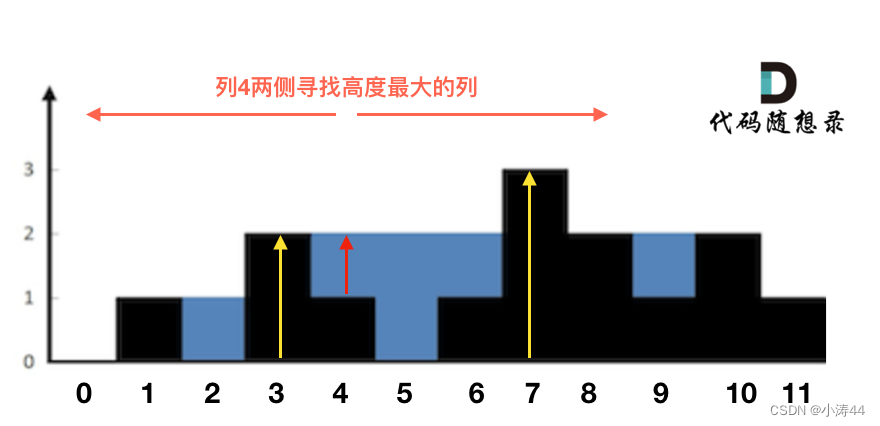
寻找每一处两侧最高的列，按列计算雨水高度并相加，每次都向两边遍历有太多重复计算，优化方法是直接用数组存好左最高和右最高列的值

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() <= 2) return 0;
        vector<int> maxLeft(height.size(), 0);
        vector<int> maxRight(height.size(), 0);
        int size = maxRight.size();

        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i < size; i++) {
            maxLeft[i] = max(height[i], maxLeft[i - 1]);
        }
        // 记录每个柱子右边柱子最大高度
        maxRight[size - 1] = height[size - 1];
        for (int i = size - 2; i >= 0; i--) {
            maxRight[i] = max(height[i], maxRight[i + 1]);
        }
        // 求和
        int sum = 0;
        for (int i = 0; i < size; i++) {
            int count = min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) sum += count;
        }
        return sum;
    }
};

单调栈

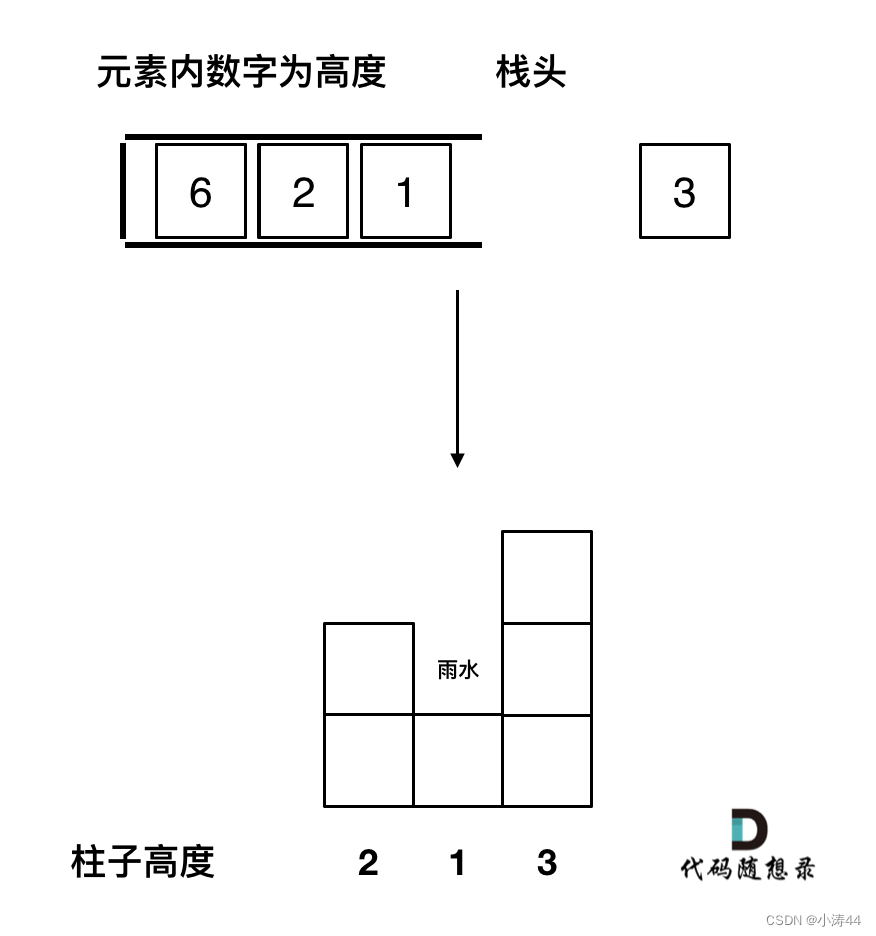
依然是单调递增栈，当大于栈顶的时候，当前高度是右边第一个高，栈顶是mid，第二栈顶正好是左边第一高，根据h*w就可以算出总雨水高度（按行计算），需要注意的是，相同的元素也压入栈对于雨水计算无影响

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> st;
        st.push(0);
        int sum = 0;
        for(int i = 1; i < height.size(); i++){
            if(height[i] <= height[st.top()]){
                st.push(i);
            }else{
                while(!st.empty() && height[i] > height[st.top()]){
                    int mid = st.top();  // 记录当前元素
                    st.pop();            // 弹出方便取第二
                    if(!st.empty()){     // 只要取top就要判空
                        int h = min(height[i], height[st.top()]) - height[mid];
                        int w = i - st.top() - 1;
                        sum += h * w;
                    }
                }
                st.push(i);
            }
        }
        return sum;
    }
};

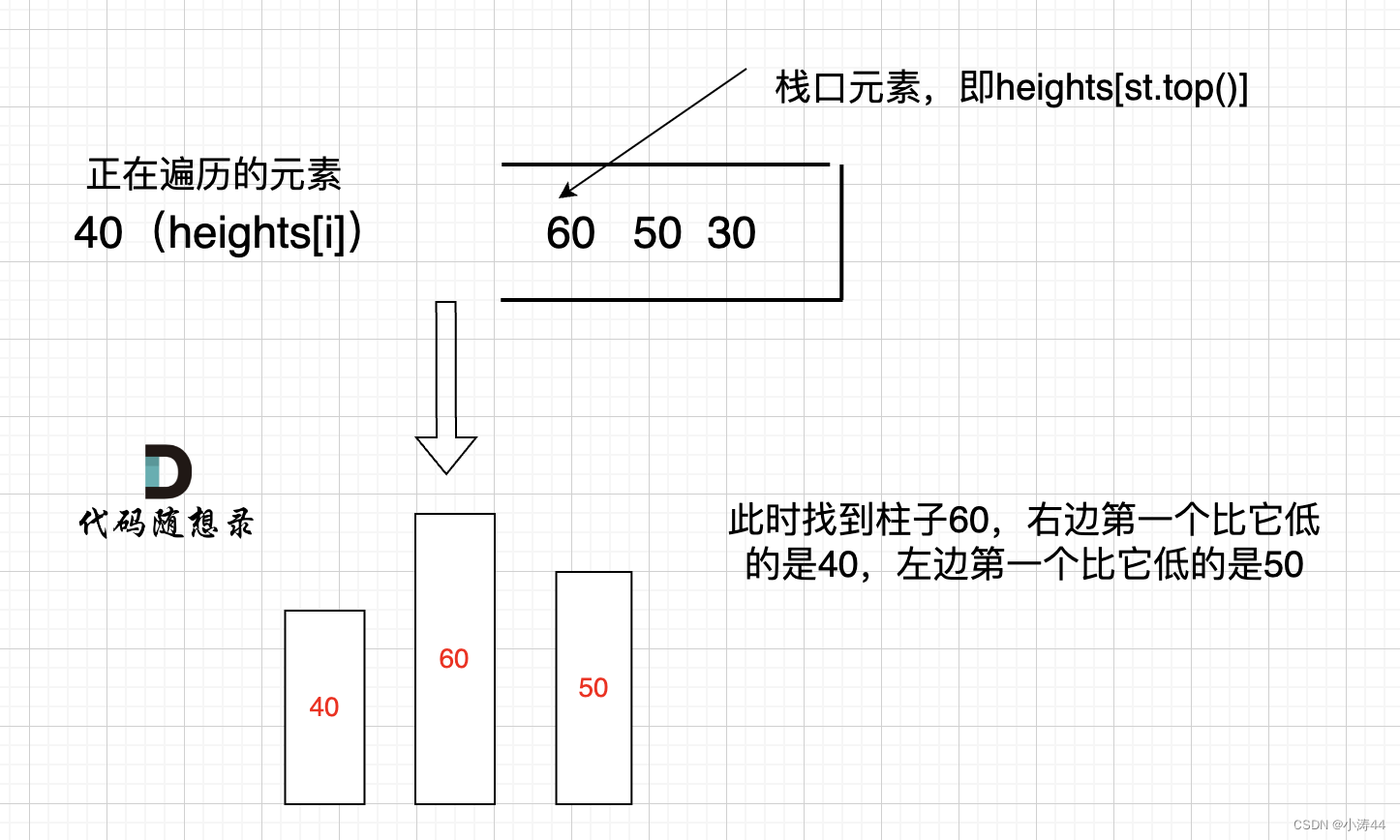
84. 柱状图中最大的矩形 - 力扣（LeetCode）

整体思路和接雨水类似，区别：前后补0、单调递减栈、计算矩形面积方式

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int sum = 0;
        heights.insert(heights.begin(), 0);  // 前加0
        heights.push_back(0);                // 后加0
        stack<int> st;                       // 递减栈
        st.push(0);
        for(int i = 1; i < heights.size(); i++){
            if(heights[i] >= heights[st.top()]){
                st.push(i);
            }else{
                while(!st.empty() && heights[i] < heights[st.top()]){
                    int mid = st.top();
                    int right = i;
                    st.pop();
                    if(!st.empty()){
                        int left = st.top();
                        int w = right - left - 1;
                        int h = heights[mid];
                        sum = max(sum, w * h);
                    }
                }
                st.push(i);
            }
        }
        return sum;
    }
};