---

---

什么是区间Dp

区间Dp指的是某些问题可以用区间来划分解决。

---

AcWing 282. 石子合并

题目链接：穿梭时间的画面的钟

---

题意分析

从一排石子中选择相邻的两堆进行合并，要求两堆之和最小。

---

思路解析

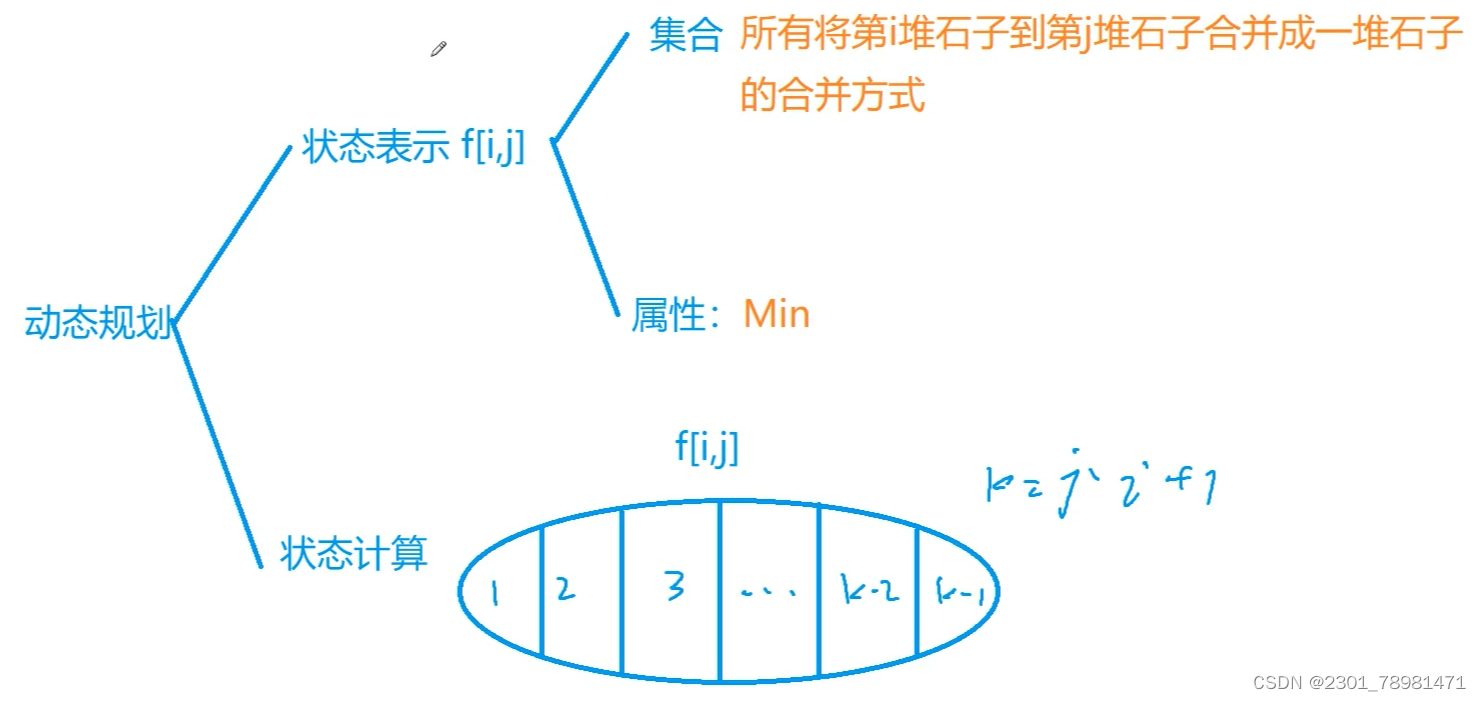
状态表示

二维状态表示，分别表示左右端点，也就是划分出了一个区间 $[i,j]$，代表的集合就是在这个区间里合并石子的代价，属性则是取最小值。

状态计算

最重要的是状态计算：如何对区间的最小代价进行计算呢？

我们将问题往回退一步：我们最终是对两堆石子进行合并，这个代价是死的，就是区间内所有石子的重量和。我们设两堆石子的分解点是 $k$，那么问题又来了，怎么确定 $k$ 在哪？我们从头往后遍历，找 $[l,k]$ 和 $[k+1,r]$的最小代价，怎么找？再往后退一步：……
最后我们可以发现，我们只需要拆解第一步，Dp就会自动往后递归，帮我们找到想要的结果。

---

CODE

#include <iostream>  
#include <cstring>  
#include <algorithm>  
  
using namespace std;  
  
const int N = 3e5 + 10; // 定义常量N，表示数组的最大长度  
int a[N], s[N]; // 定义整数数组a和前缀和数组s  
int f[N][N]; // 定义二维数组f，用于动态规划计算最大和  
  
int main() // 主函数开始  
{  
    int n; // 定义整数n，表示接下来要输入的整数的数量  
    scanf("%d", &n); // 读取整数n  
  
    for(int i = 1; i <= n; ++i) // 循环读取n个整数并存储在数组a中  
    {  
        scanf("%d", &a[i]);  
        s[i] = s[i - 1] + a[i]; // 计算前缀和数组s  
    }  
  
    for(int len = 1; len <= n; ++len) // 循环计算不同长度的子数组的最大和  
    {  
        for(int i = 1; i + len - 1 <= n; ++i) // 内层循环遍历所有可能的起始位置i  
        {  
            int l = i, r = l + len - 1; // 定义左边界l和右边界r  
            for(int k = l; k <= r; ++k) // 对于每个k，计算f[l][r]的值  
            {  
            	// 更新f[l][r]的值
                f[l][r] = min(f[l][r], f[l][k] + f[k][r] + s[r] - s[l]);   
            }  
        }  
    }  
  
    cout << f[1][n] << endl; // 输出整个数组中的最大和  
  
    return 0; // 主函数结束，返回0表示程序正常结束  
}



枚举左右端点，但是左端点要从最后一个开始枚举
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 330, INF = 0x3f3f3f3f;

int a[N], s[N];
int f[N][N];

int main(){
    int n;
    scanf("%d", &n);

    for (int i = 1; i <= n; i ++ ){
        scanf("%d", &a[i]);
        s[i] = s[i - 1] + a[i];
    }

    for(int i = n; i >= 1; --i)
        for(int j = i + 1; j <= n; ++j){
            if(i == j){
                f[i][j] = 0;
                continue;
            }

            f[i][j] = INF;
            for(int k = i; k <= j; ++k){
                f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
            }
        }

    cout << f[1][n] << endl;
}

---

需要注意的问题

• 枚举区间长度时，从 $2$ 开始枚举，因为后面有一句f[i][j] = INF，如果从 $1$ 开始的话就会将f[i][i]这个区间设为INF了，这个区间意味着自己到自己需要合并的最小代价，但是只有一堆，所以是不需要合并的，也就是 $0$，那么这么做就错了。
• 枚举左右端点时要从后往前枚举，因为答案是f[1][n]，而我们从第一堆开始枚举的时候会导致后面的最小代价全都是 $0$，在过了f[1]时才会从默认的 $0$ 更新。