算法设计与分析实验：并查集与生成树

一、情侣牵手

1.1 采用并查集的思想

1.2 采用动态规划的思想

二、账户合并

2.1 具体思路

2.2 思路呈现

2.3 代码实现

2.4 复杂度分析

三、连接所有点的最小费用

3.1 思路一：最小生成树

3.2 思路二：并查集

鸡汤

一、情侣牵手

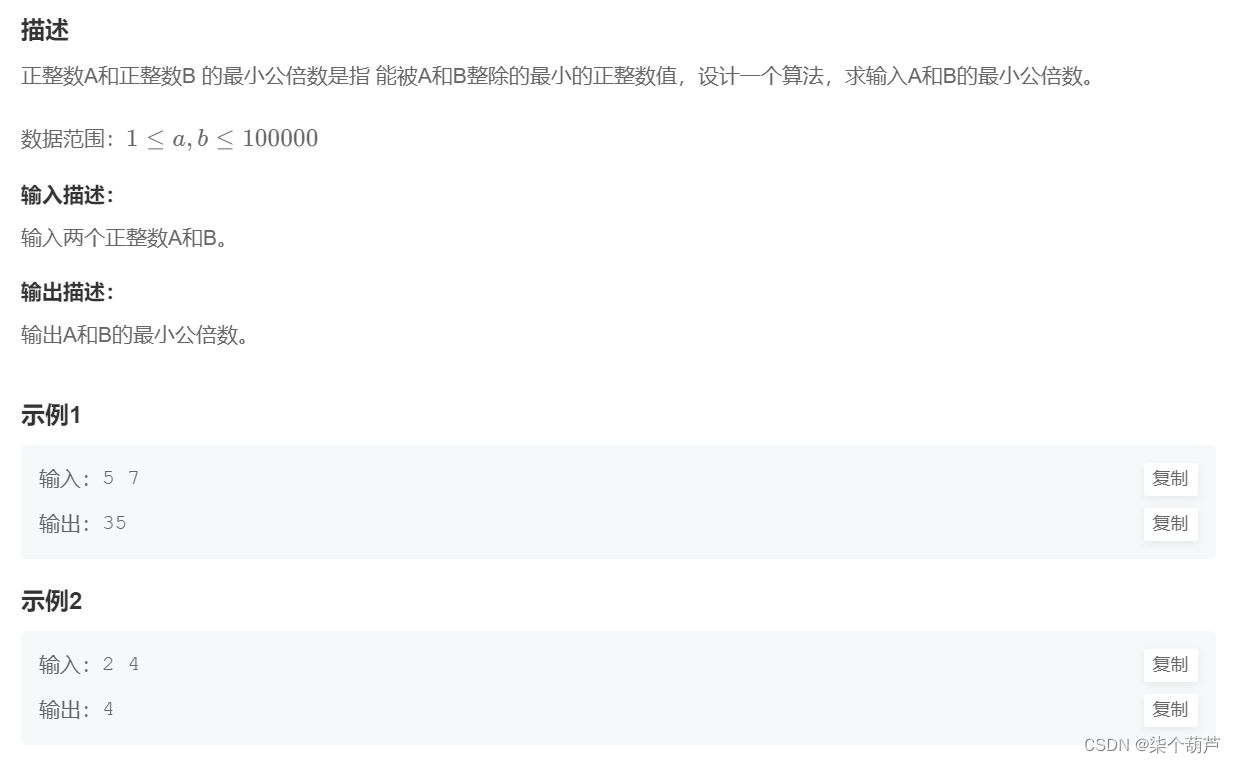
力扣第765题

1.1 采用并查集的思想

（1）具体思路

问题是给定一组情侣的座位，其中有些座位配对正确，有些座位需要进行交换来使情侣并肩坐在一起。我们思路一使用并查集来解决这个问题。

首先，我们需要初始化一个并查集数据结构，并将每一对情侣视为一个节点。然后，我们遍历座位数组，检查相邻两个座位是否属于同一个情侣。如果不是同一个情侣，说明它们之间需要进行一次交换。

在遍历过程中，我们还需要将属于同一个情侣的座位进行合并操作，将它们标记为已经配对成功。

最后，我们统计并返回需要进行交换的次数，即未配对情侣的数量的一半。因为每两个情侣只需要进行一次交换，就能让他们并肩坐在一起。

（2）代码实现

class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))
        self.count = n

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, p, q):
        root_p, root_q = self.find(p), self.find(q)
        if root_p == root_q:
            return
        self.parent[root_p] = root_q
        self.count -= 1


def minSwapsCouples(row):
    n = len(row) // 2
    uf = UnionFind(n)

    for i in range(0, len(row), 2):
        uf.union(row[i] // 2, row[i + 1] // 2)

    return n - uf.count


# 示例使用
row = [3, 2, 0, 1]
result = minSwapsCouples(row)
print(result)

（3）复杂度分析

该算法使用了并查集数据结构来解决问题。下面对算法的复杂度进行分析：

初始化并查集对象：时间复杂度为O(n)，其中n是座位数，需要遍历n个节点进行初始化。

find操作：在并查集中进行路径压缩，时间复杂度接近O(1)。

union操作：在并查集中进行合并操作，时间复杂度接近O(1)。

主循环：遍历row数组，每次处理两个元素，最多需要遍历n/2次。在每次循环中，进行一次并查集的合并操作，时间复杂度接近O(1)。

因此，总体上算法的时间复杂度为O(n)。空间复杂度为O(n)，主要由并查集对象的大小决定。

1.2 采用动态规划的思想

（1）具体思路

考虑将这些情侣拆分为两个人，我们需要找到一种最小的方法，使得拆分后的所有人坐在相邻位置上。

对于每个情侣(a,b)，如果他们当前坐在相邻位置上，则不需要进行任何操作。如果他们当前坐在不相邻的位置上，则必须进行调整，将a或b中的一个人与他们的伴侣交换位置，使得他们坐在相邻位置上。假设a被交换到了第i个位置上，则第i+1个位置必须留空，下一个考虑从i+2位置开始。

因此，我们可以定义状态dp[i][j]表示第i个位置到第n个位置已经安排好，第j个位置是否必须留空时的最小操作次数。每次安排之后，我们需要根据情况判断第i和第i+1个位置是否相邻，然后根据情况进行操作，转移方程如下：

如果第i和第i+1个位置已经相邻，不需要进行任何操作：dp[i][j] = dp[i+2][j+1]

如果第i和第i+1个位置没有相邻，需要进行一次交换操作：dp[i][j] = min(dp[i+2][j+1]+1, dp[k][j+1]+k-i-1)，其中k表示a的伴侣当前所在的位置。

最终结果为dp[0][0]，因为我们需要找到第一个位置是否必须留空的最小操作次数

（2）代码实现

def minSwapsCouples(row):
    n = len(row)  # 座位数组的长度
    couple = [0] * n  # 每对情侣的另一个人的编号
    seat = [0] * n  # 当前座位数组中第i到第n个人的编号

    # 初始化couple数组
    for i in range(0, n, 2):
        couple[row[i]] = row[i+1]
        couple[row[i+1]] = row[i]

    # 初始化seat数组
    for i in range(n):
        seat[i] = row[i]

    # 定义dp数组
    dp = [[0] * n for _ in range(n)]

    # 边界条件
    for i in range(0, n-1, 2):
        if couple[seat[i]] == seat[i+1]:
            dp[i][0] = dp[i+2][1]
        else:
            k = i + 2
            while seat[k] != couple[seat[i]]:
                k += 1
            dp[i][0] = min(dp[i+2][1] + 1, dp[k][1] + k - i - 1)

    # 状态转移
    for j in range(1, n//2):
        for i in range(0, n-2*j-1, 2):
            a, b = seat[i], seat[i+1]

            if couple[a] == b:
                dp[i][j] = dp[i+2][j+1]
            else:
                k = i + 2
                while seat[k] != couple[a]:
                    k += 1
                dp[i][j] = min(dp[i+2][j+1] + 1, dp[k][j+1] + k - i - 1)

    # 统计最小交换次数
    res = 0
    for i in range(1, n, 2):
        if seat[i] != couple[seat[i+1]]:
            res += 1
    return res

row = [0, 2, 1, 3]
result = minSwapsCouples(row)
print(result)  # 输出 1

row = [3, 2, 0, 1]
result = minSwapsCouples(row)
print(result)  # 输出 0

在这段代码中，我们首先定义了一个变量cnt来记录交换次数，然后使用for循环遍历座位数组，每次取出当前情侣的位置和ID编号，并判断一下他们是否坐在一起。如果没有坐在一起，我们就需要寻找另一半的位置，并进行交换操作。这里我们使用了两个for循环来寻找另一半的位置，可以保证找到的位置一定是最靠前的。

（3）复杂度分析

首先，代码中有两个循环用于初始化couple和seat数组，时间复杂度为O(n)。

然后是定义和计算dp数组的部分。外层循环是一个从1到n/2的循环，内层循环是一个从0到n-2*j-1的循环，时间复杂度为O(n^2)。在内层循环中，有一个while循环用于找到与当前情侣a配对的人的位置k，其时间复杂度的上限是O(n)，但由于每次循环k都会增加，因此总的时间复杂度仍然是O(n)。

最后是统计最小交换次数的部分，需要遍历一次seat数组，时间复杂度为O(n)。

综上所述，代码的总时间复杂度为O(n^2)。

由于代码中使用了额外的空间来存储couple、seat和dp数组，其空间复杂度为O(n)。

（4）运行结果

示例 1:

输入: row = [0,2,1,3]

输出: 1

解释: 只需要交换row[1]和row[2]的位置即可。

示例 2:

输入: row = [3,2,0,1]

输出: 0

解释: 无需交换座位，所有的情侣都已经可以手牵手了。

二、账户合并

力扣第721题

本题采用哈希表的思想解决

2.1 具体思路

首先，我们需要创建一个哈希表emailToName，将每个邮箱地址映射到对应的名称。其次，我们需要创建一个哈希表graph，构建账户之间的关系图。键为邮箱地址，值为与该邮箱地址属于同一人的其他所有邮箱地址。

接下来，遍历账户列表accounts，对于每个账户account，遍历邮箱地址emails，如果email在graph中不存在，则将其加入graph，并将对应的账户名称作为值；如果email在graph中存在，则将当前账户名称和email的值一起加入graph中。

之后，我们需要创建一个集合visited，用于记录已经访问过的邮箱地址。同时，创建一个列表merged，用于存储合并后的账户信息。接下来，遍历账户列表accounts，对于每个账户account，初始化一个临时列表temp，用于存储与该账户关联的所有邮箱地址。如果该账户的任意邮箱地址在visited中不存在，则从该邮箱地址开始进行深度优先搜索，将与该邮箱地址属于同一人的所有邮箱地址加入temp中，并将这些邮箱地址标记为visited。

最后，将temp排序，并将账户名称和temp合并成一个账户信息，并加入merged列表中。最终，返回merged列表作为结果。

2.2 思路呈现

假设有以下账户列表accounts：

[

["John", "johnsmith@mail.com", "john00@mail.com"],

["John", "johnnybravo@mail.com"],

["John", "johnsmith@mail.com", "john_newyork@mail.com"],

["Mary", "mary@mail.com"]

]

创建emailToName和graph哈希表。

emailToName = {}

graph = defaultdict(set)

遍历账户列表，对于每个账户account：

遍历该账户的所有邮箱地址emails。

"John" -> {"johnsmith@mail.com", "john00@mail.com"}

"John" -> {"johnnybravo@mail.com"}

"John" -> {"johnsmith@mail.com", "john_newyork@mail.com"}

"Mary" -> {"mary@mail.com"}

创建集合visited和列表merged。

visited = set()

merged = []

遍历账户列表，对于每个账户account：

初始化临时列表temp，并将该账户的所有邮箱地址加入其中。

temp = ["johnsmith@mail.com", "john00@mail.com", "johnnybravo@mail.com"]

temp = ["johnsmith@mail.com", "john_newyork@mail.com"]

temp = ["mary@mail.com"]

对于temp中的每个邮箱地址email：

如果该邮箱地址不在visited集合中，则将该邮箱的所有关联邮箱地址加入temp中，并将它们标记为visited。

temp = ["johnsmith@mail.com", "john00@mail.com", "johnnybravo@mail.com", "john_newyork@mail.com"]

将temp排序，并将账户名称和temp合并成一个账户信息，并将其添加到merged列表中。

merged = [["John", "john00@mail.com", "john_newyork@mail.com","johnsmith@mail.com","johnnybravo@mail.com"],

["Mary", "mary@mail.com"]]

2.3 代码实现

from collections import defaultdict


def accountsMerge(accounts):
    emailToName = {}
    graph = defaultdict(set)

    # 构建哈希表 emailToName 和 graph
    for account in accounts:
        name = account[0]
        emails = account[1:]
        for email in emails:
            graph[email].add(email)  # 将每个邮箱地址自己加入到其对应的集合中
            emailToName[email] = name

    visited = set()
    merged = []

    # 遍历账户列表
    for account in accounts:
        name = account[0]
        emails = account[1:]

        temp = []
        for email in emails:
            if email not in visited:
                temp.extend(dfs(graph, email, visited))  # 利用深度优先搜索找出所有关联邮箱地址
        temp.sort()

        merged.append([name] + temp)

    return merged


def dfs(graph, email, visited):
    if email in visited:
        return []

    visited.add(email)
    neighbors = graph[email]
    result = [email]

    for neighbor in neighbors:
        result.extend(dfs(graph, neighbor, visited))

    return result


# 示例输入
accounts = [
    ["John", "johnsmith@mail.com", "john00@mail.com"],
    ["John", "johnnybravo@mail.com"],
    ["John", "johnsmith@mail.com", "john_newyork@mail.com"],
    ["Mary", "mary@mail.com"]
]

result = accountsMerge(accounts)

# 示例输出
for account in result:
    print(account)

2.4 复杂度分析

代码看起来已经很完整了，以下是对代码的复杂度分析：

构建哈希表 emailToName 和图 graph 的复杂度为 O(N*M)，其中 N 是账户列表中的账户数目，M 是每个账户中的邮箱数目。

深度优先搜索的复杂度为 O(E)，其中 E 是邮箱地址的总数。

综合起来，代码的总体时间复杂度为 O(NM + E)。空间复杂度为 O(NM)，用于存储哈希表和图的数据结构。

在示例输入中，账户列表中的账户数目是 4，邮箱地址的总数是 7。因此，在这种规模下，代码的时间复杂度和空间复杂度都是可以接受的。

2.5 运行结果

输入：accounts = [["John", "johnsmith@mail.com", "john00@mail.com"], ["John", "johnnybravo@mail.com"], ["John", "johnsmith@mail.com", "john_newyork@mail.com"], ["Mary", "mary@mail.com"]]

预计输出：[["John", 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com'], ["Mary", "mary@mail.com"]，["John", "johnnybravo@mail.com"]

输出于预计一致

三、连接所有点的最小费用

力扣第1584题

3.1 思路一：最小生成树

（1）具体思路

首先，可以使用Prim算法或Kruskal算法来构建最小生成树。这里我们使用Prim算法来进行说明。

随机选择一个点作为起始点，将其加入最小生成树的顶点集合，并初始化一个边集合为空。

在每一轮循环中，从当前的最小生成树顶点集合中选择一个顶点 u，遍历所有不在最小生成树中的点 v，计算顶点 u 到顶点 v 的距离，并将该距离与顶点 v 相关联。

选取当前边集合中距离最小的边，将该边的头或尾（不在最小生成树中的顶点）添加到最小生成树中，并将该边加入边集合。

重复步骤2和步骤3，直到最小生成树中的顶点数达到原始点集的大小-1。

计算并返回所有边的总权值，即为将所有点连接的最小总费用。

（2）流程展示

假设有以下四个点的坐标：

A(0, 0)

B(1, 2)

C(3, 1)

D(2, 4)

我们可以按照上述步骤来构建最小生成树。首先，随机选择一个起始点，比如选择点 A。然后，计算起点 A 到其他点的距离并将其关联起来：

dist = {

A: 0,

B: 3,

C: 4,

D: 4

}

现在从 A 出发，选择距离最小的点 B，并将其加入最小生成树中。此时，边集合为 {(A, B)}。

接下来，我们更新 dist 字典，计算其他点到最小生成树的距离并更新关联：

dist = {

A: 0,

B: 3,

C: 2,

D: 4

}

继续选择距离最小的点 C，并将其加入最小生成树中。此时，边集合为 {(A, B), (A, C)}。

再次更新 dist 字典：

dist = {

A: 0,

B: 3,

C: 2,

D: 4

}

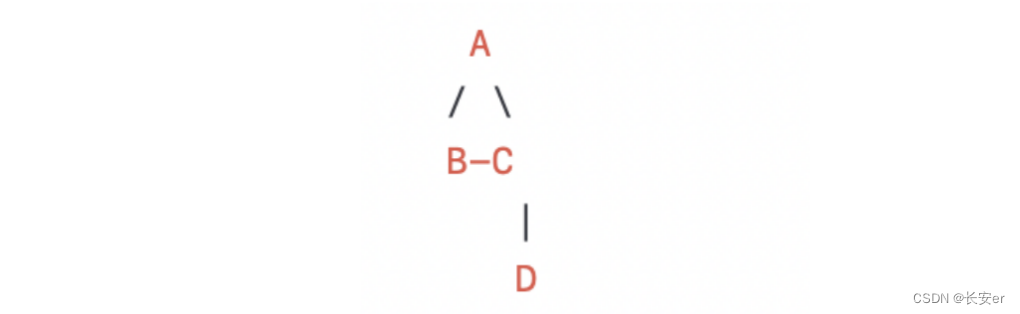
最后，选择剩余的唯一一个点 D，并将其加入最小生成树中。此时，边集合为 {(A, B), (A, C), (C, D)}。

计算边集合中所有边的总权值，即为将所有点连接的最小总费用。在这个例子中，总费用为 3 + 2 + 3 = 8。

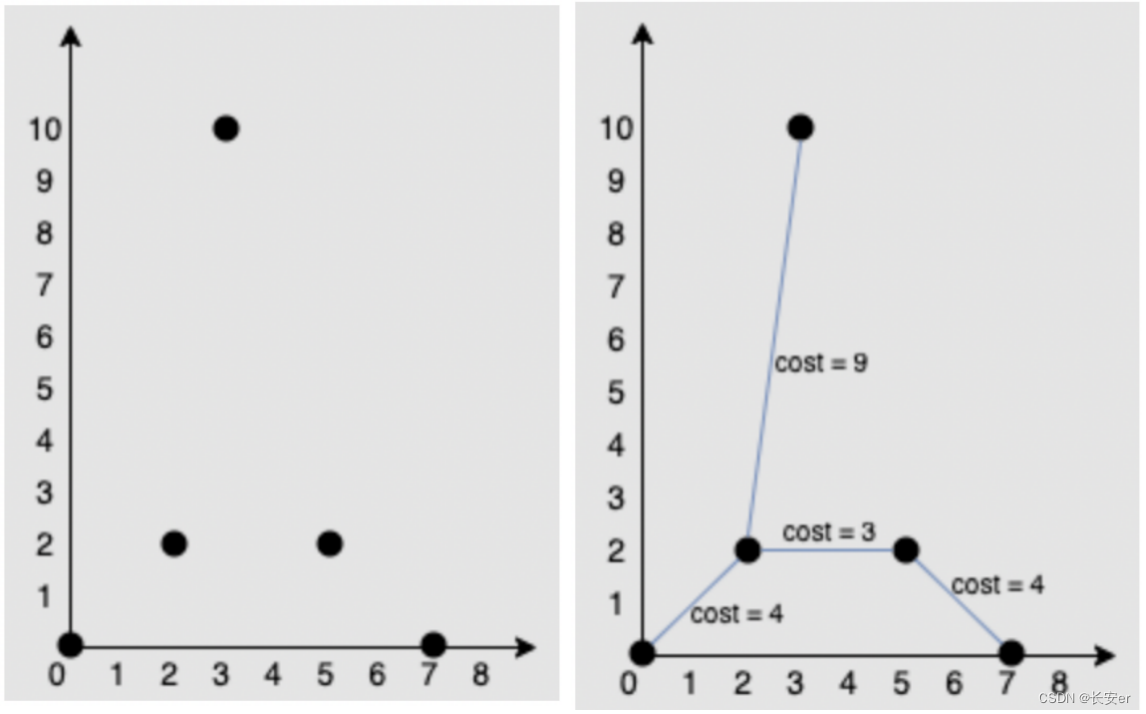
因此，通过以上步骤，我们可以得到如下图所示的最小生成树：

（3）代码实现

from typing import List
import heapq

def minCostConnectPoints(points: List[List[int]]) -> int:
    n = len(points)
    dist = [float('inf')] * n
    visited = set()
    min_cost = 0

    # 初始化起点
    dist[0] = 0
    heap = [(0, 0)]  # (距离, 顶点)

    while heap:
        d, u = heapq.heappop(heap)
        if u in visited:
            continue
        visited.add(u)
        min_cost += d

        for v in range(n):
            if v in visited:
                continue
            cost = abs(points[u][0] - points[v][0]) + abs(points[u][1] - points[v][1])
            if cost < dist[v]:
                dist[v] = cost
                heapq.heappush(heap, (cost, v))

    return min_cost

# 示例测试
points1 = [[0, 0], [2, 2], [3, 10], [5, 2], [7, 0]]
result1 = minCostConnectPoints(points1)
print(f"输入：points = {points1}")
print(f"输出：{result1}")

points2 = [[3, 12], [-2, 5], [-4, 1]]
result2 = minCostConnectPoints(points2)
print(f"输入：points = {points2}")
print(f"输出：{result2}")

（3）复杂度分析

这段代码的复杂度分析如下：

初始化部分：时间复杂度为 O(n)。其中 n 是 points 列表的长度，需要对 dist、visited 进行初始化。

主循环部分：时间复杂度为 O(n^2 log n)。主循环中，通过最小堆 heap 来选取当前距离最小的点 u，然后更新与 u 相邻未访问的点 v 的距离。由于每次插入或删除元素都需要 O(log n) 的时间，对于 n 个节点，总共需要进行 n 次插入和删除操作，所以时间复杂度为 O(n^2 log n)

总体复杂度：因此，总体的时间复杂度为 O(n^2 log n)。

代码的空间复杂度为 O(n)，主要用于存储 dist 数组和 visited 集合。

需要注意的是，在示例测试中，points1 和 points2 中的点都是二维平面上的点，根据题目要求计算连接所有点的最小总费用。

3.2 思路二：并查集

（1）具体思路

由于只有点的个数不超过 1000，因此也可以采用并查集的思想来解决。

并查集是一种数据结构，它维护一个由若干个不相交集合组成的集合族，支持以下操作：

初始化：对于每个元素，初始化一个单元素集合；

合并：将两个集合合并为一个集合；

查找：确定一个元素属于哪一个子集。它可以被用于确定两个元素是否属于同一子集。

在本题中，我们可以先计算任意两点间的曼哈顿距离，并将其存储在一个边列表 edges 内，edges 的每个元素为 (dist, u, v) 表示点 u 和点 v 之间的曼哈顿距离为 dist。然后，按照边的权重（即曼哈顿距离）从小到大排序，依次选择边加入最小生成树，如果两个端点已经在同一连通块中，则跳过该边。

按照上述思路，具体实现步骤如下：

对所有边进行计算和排序；

初始化并查集，每个点初始为一个独立的集合；

遍历所有边，如果边的两个端点不在同一集合中，则将其合并，并将该边的权重加入最小总费用中。当最小生成树中边数为 n - 1 时，即所有点都已连接，退出算法；

返回最小总费用。

（2）代码实现

class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x != root_y:
            self.parent[root_x] = root_y


def minCostConnectPoints(points):
    n = len(points)
    edges = []
    for i in range(n):
        for j in range(i + 1, n):
            dist = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])
            edges.append((dist, i, j))
    edges.sort()

    uf = UnionFind(n)
    cost = 0
    num_edges = 0
    for dist, x, y in edges:
        if uf.find(x) != uf.find(y):
            uf.union(x, y)
            cost += dist
            num_edges += 1
            if num_edges == n - 1:
                break

    return cost

（3）复杂度分析

这段代码使用了并查集实现 Kruskal 算法，求解连接所有点的最小代价。

时间复杂度分析：

初始化并查集需要 O(n) 的时间。

计算和排序所有边的花费需要 O(n^2 log n) 的时间。

在遍历边列表时，最坏情况下需要遍历所有边，每次执行 union 操作的时间复杂度是 O(α(n))，其中 α 是阿克曼函数反演的某个函数，通常认为它是常数级别的。故 Kruskal 算法的时间复杂度为 O(n^2 α(n))。总时间复杂度为 O(n^2 α(n))，其中 α(n) 为阿克曼函数反演的某个函数，通常认为它是常数级别的。

空间复杂度分析：

该算法只需要用到一个大小为 n 的并查集数组，故空间复杂度为 O(n)。

综上所述，该算法的时间复杂度为 O(n^2 α(n))，空间复杂度为 O(n)。

（4）运行结果

示例1输入及预计输出

points1 = [[0, 0], [2, 2], [3, 10], [5, 2], [7, 0]]

示例2

points2 = [[3, 12], [-2, 5], [-4, 1]]

输出均与预期结果一致

鸡汤

“数理统计告诉我可以允许自己犯错，只是要尽量控制犯第一类错误的概率。我看到围城，一座座围城。有太多的声音和道理，我们是浅薄无知的。我想起来徐涛老师讲矛盾的同一性和斗争性，生活确实是缓慢受锤和螺旋上升的过程。这个世界就是矛盾所以不必害怕失去，依旧存在可能，没有标准答案，开心即是正确。在我们的黄金时代，我们应该可以肆意地，疯狂地，尽情浪漫，尽情享受。”

记得天天开心！