Cache Lab：Part B- 32 ×32【分块算法】

news2024/9/23 11:13:57

任务描述

在B部分中，您将在trans.c中编写一个转置函数，从而导致尽可能少的miss。缓存的参数位 (s = 5, E = 1, b = 5)。三种测试用例的矩阵大小分别为：
        • 32 × 32 (M = 32, N = 32)
        • 64 × 64 (M = 64, N = 64)
        • 61 × 67 (M = 61, N = 67)

规定：仅使用12个局部变量，不能使用递归，不能修改A数组（可任意修改B数组），不允许使用malloc

分析

write up (Page 6)提到

“你的代码只需要针对这三种情况是正确的，并且你可以针对这三种情况进行专门优化。特别是，你的函数完全可以显式检查输入大小并实现针对每种情况优化的单独代码。 ”

那就对三种测试用例分别进行分块上的设计。本篇先完成32×32。

下图是分块情况，每一个小格代表一个block（由前提条件b=5，得出一个块是32字节，由于是int数组，所以一个block能存8个元素）

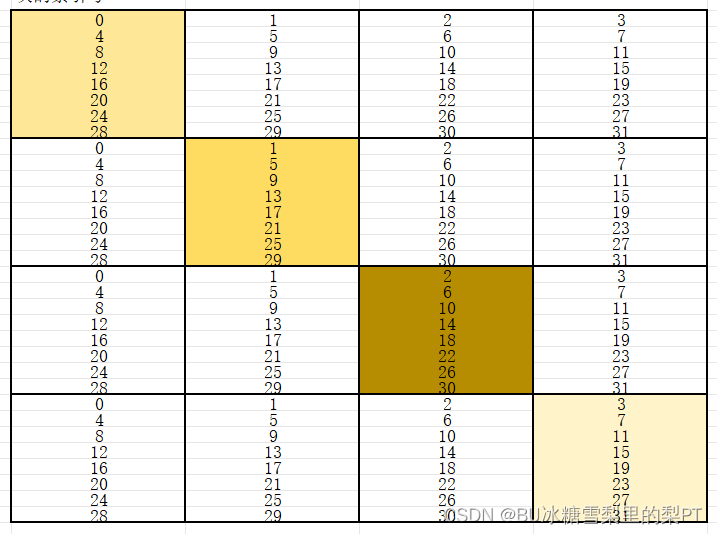
上面是16个大块。

转置时依次扫描大块1~16，将块内元素转置后放在数组B对应的位置。可以发现，除了对角块，其余都是没有冲突未命中的。

32 × 32 (M = 32, N = 32)

上述简单分块

现象：m=344，而满分是m<300

修改思路：对角线的优化

int i, j, k, q, tmp;
if (M == 32 && N == 32)
{
	for (k = 0; k < 4; k++)
	{
		for (q = 0; q < 4; q++)
		{
			for (i = 0; i < 8; i++)
			{
				for (j = 0; j < 8; j++)
				{
					tmp = A[k * 8 + i][q * 8 + j];
					B[q * 8 + j][k * 8 + i] = tmp;
				}
			}
		}
	}
}

尝试优化1：给对角线上的块再次细分块

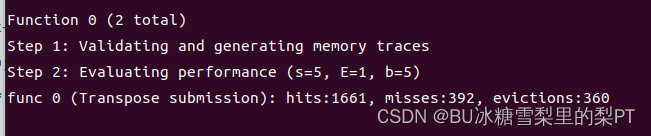
现象：更差（m=392）

int i, j, k, q, i2, j2, k2, q2, tmp;
if (M == 32 && N == 32)
{
	for (k = 0; k < 4; k++)
	{
		for (q = 0; q < 4; q++)
		{
			if (k == q)
			{
				for (k2 = 0; k2 < 2; k2++)
				{
					for (q2 = 0; q2 < 2; q2++)
					{
						for (i2 = 0; i2 < 4; i2++)
						{
							for (j2 = 0; j2 < 4; j2++)
							{
								tmp = A[k * 8 + k2 * 4 + i2][q * 8 + q2 * 4 + j2];
								B[q * 8 + q2 * 4 + j2][k * 8 + k2 * 4 + i2] = tmp;
							}
						}

					}
				}
			}
			else
			{
				for (i = 0; i < 8; i++)
				{
					for (j = 0; j < 8; j++)
					{
						tmp = A[k * 8 + i][q * 8 + j];
						B[q * 8 + j][k * 8 + i] = tmp;
					}
				}
			}

		}
	}
}

尝试优化2：对角块依次错位法

具体来说，转置完的1号大块存在6号大块，6号存在11号，11号存在16号。16号进行普通转置。

现象：变好，m=305（满分300，你在卡我：(

int i, j, k, q, tmp;
if (M == 32 && N == 32)
{
	for (k = 0; k < 4; k++)
	{
		for (q = 0; q < 4; q++)
		{
			if (k == q && k != 3)
			{
				for (i = 0; i < 8; i++)
				{
					for (j = 0; j < 8; j++)
					{
						tmp = A[k * 8 + i][q * 8 + j];
						B[q * 8 + 8 + j][k * 8 + 8 + i] = tmp;
					}
				}
				for (i = 0; i < 8; i++)
				{
					for (j = 0; j < 8; j++)
					{
						tmp = B[k * 8 + i + 8][q * 8 + j + 8];
						B[k * 8 + i][q * 8 + j] = tmp;
					}
				}
			}
			else
			{
				for (i = 0; i < 8; i++)
				{
					for (j = 0; j < 8; j++)
					{
						tmp = A[k * 8 + i][q * 8 + j];
						B[q * 8 + j][k * 8 + i] = tmp;
					}
				}
			}
		}
	}
}

尝试优化3：对角块两两交换

具体来说，A的1号转置完成后存到B的6号，A的6号转置完存到B的1号去。然后，B的1号和6号交换。11号和16号同理。

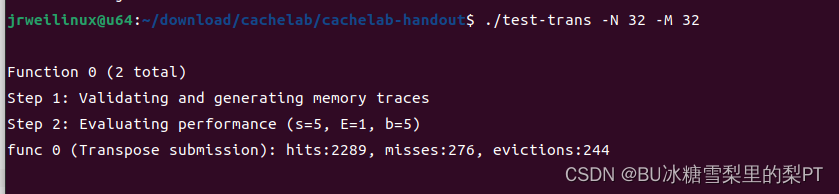
现象：m=276，成功。

int i, j, k, q, tmp;
if (M == 32 && N == 32)
{
	for (k = 0; k < 4; k++)
	{
		for (q = 0; q < 4; q++)
		{
			if (k == q && k % 2 == 0)
			{
				for (i = 0; i < 8; i++)
				{
					for (j = 0; j < 8; j++)
					{
						tmp = A[k * 8 + i][q * 8 + j];
						B[q * 8 + 8 + j][k * 8 + 8 + i] = tmp;
					}
				}
			}
			else if (k == q && k % 2 == 1)
			{
				for (i = 0; i < 8; i++)
				{
					for (j = 0; j < 8; j++)
					{
						tmp = A[k * 8 + i][q * 8 + j];
						B[q * 8 - 8 + j][k * 8 - 8 + i] = tmp;
					}
				}
				for (i = 0; i < 8; i++)
				{
					for (j = 0; j < 8; j++)
					{
						tmp = B[k * 8 + i][q * 8 + j];
						B[k * 8 + i][q * 8 + j] = B[k * 8 - 8 + i][q * 8 - 8 + j];
						B[k * 8 - 8 + i][q * 8 - 8 + j] = tmp;
					}
				}
			}
			else
			{
				for (i = 0; i < 8; i++)
				{
					for (j = 0; j < 8; j++)
					{
						tmp = A[k * 8 + i][q * 8 + j];
						B[q * 8 + j][k * 8 + i] = tmp;
					}
				}
			}
		}
	}
}