获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 基本概念
- 多项式时间
- 指数时间
- P问题(多项式问题)
- NP问题(非确定性多项式问题)
- 暴力穷举法
- 动态规划
- P与NP关系:
- 作业车间调度问题是典型的NP难问题
P和NP问题是计算机科学中的两个重要的问题,涉及到计算问题的复杂性和可解性。这两个问题都与算法的效率和时间复杂度有关。
基本概念
多项式时间
多项式时间指的是算法的运行时间与问题规模之间存在多项式关系。更具体地说,如果一个算法的运行时间可以表示为问题规模的某个多项式函数,那么这个算法在多项式时间内运行。通常用 O ( n k ) O(n^k) O(nk)来表示多项式时间,其中n是问题的输入规模(通常表示为输入的大小),k是一个常数。
例子:
- O ( n ) O(n) O(n)表示线性时间,算法的运行时间与输入规模成线性关系。
- O ( n 2 ) O(n^2) O(n2)表示平方时间,算法的运行时间与输入规模的平方成正比。
- O ( n 3 ) O(n^3) O(n3)表示立方时间,算法的运行时间与输入规模的立方成正比。
多项式时间算法通常被认为是高效的,因为它们在处理大规模问题时的运行时间增长相对较慢。
指数时间
指数时间指的是算法的运行时间与问题规模之间存在指数关系。如果一个算法的运行时间增长迅速,超过了问题规模的指数函数,那么这个算法就是指数时间的。通常用 O ( 2 n ) O(2^n) O(2n)表示指数时间,其中n是问题的输入规模。
例子:
- O ( 2 n ) O(2^n) O(2n)表示指数时间,算法的运行时间随着输入规模的增加呈指数级增长。
指数时间算法通常非常慢,特别是在处理大规模问题时,因为它们的运行时间增长非常迅猛。在实际应用中,指数时间算法通常只适用于小规模问题,因为对于大规模问题,它们的运行时间可能会变得不切实际。
P问题(多项式问题)
P问题(Polynomial Problem)是指那些可以在多项式时间内(即问题规模的多项式函数时间内)解决的问题。简单来说,如果一个问题是P问题,那么存在一个算法,其运行时间的上限是输入规模的多项式函数,也就是说,对于P问题,存在一个多项式函数 f ( n ) f(n) f(n),其中n是输入规模,算法的运行时间是 O ( f ( n ) ) O(f(n)) O(f(n))。大多数常见的计算问题,例如排序、搜索和数学运算,都属于P问题。这些问题可以有效地通过计算机算法来解决,而且在合理的时间内。
假设有一个排序问题,你需要对一个包含n个整数的数组进行排序。一个典型的排序算法是冒泡排序。在冒泡排序中,每次比较相邻的两个元素并交换它们,然后再次遍历数组,重复这个过程,直到整个数组排序完成。这个算法的时间复杂度是 O ( n 2 ) O(n^2) O(n2),其中n是数组的大小。这意味着算法的运行时间与数组大小的平方成正比。这个问题是一个P问题,因为存在一个多项式函数 n 2 n^2 n2来描述算法的运行时间。
冒泡排序的基本思想是从左到右不断比较相邻两个元素,如果它们的顺序不正确(即前面的元素大于后面的元素),则交换它们,将较大的元素“冒泡”到右侧。这个过程一直重复,直到没有需要交换的元素为止。下面为冒泡排序的Python代码。
def bubble_sort(arr):
n = len(arr)
# 遍历数组元素,执行n-1次
for i in range(n - 1):
# 每次遍历从头开始,将较大的元素逐个向后交换
for j in range(0, n - 1 - i):
if arr[j] > arr[j + 1]:
# 交换arr[j]和arr[j + 1]的值
arr[j], arr[j + 1] = arr[j + 1], arr[j]
可以看到,上述代码包含两层循环。
外层循环迭代n-1次,表示当剩余一个元素时就没有必要移动了。
内层循环迭代的次数是不同的。在第一次迭代中,它需要比较n-1次。在第二次迭代中,它需要比较n-2次,依此类推。
因此,总的比较次数可以表示为:
(n-1) + (n-2) + (n-3) + ... + 1= n(n-1)/2
对于每一次比较,如果需要交换,就会执行一次交换操作。最坏情况下,每次比较都需要交换,因此交换的次数与比较的次数相等,都是 O ( n 2 ) O(n^2) O(n2)。
所以冒泡排序的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
NP问题(非确定性多项式问题)
NP问题(Non-deterministic Polynomial Problem)是指那些可以在多项式时间内验证给定解的问题。也就是说,如果你有一个候选解,你可以在多项式时间内检查它是否是正确的解。然而,尚未找到一种有效的算法来在多项式时间内解决所有NP问题。如果某个问题是NP问题,那么如果你提供一个猜测的解,你可以在多项式时间内验证它是否正确。典型的NP问题包括旅行商问题和背包问题。
旅行商问题(Traveling Salesman Problem,TSP)是一个组合优化问题,它的时间复杂度在一般情况下是指数级别的。TSP的时间复杂度取决于问题的规模(城市数量)和求解方法。
暴力穷举法
如果使用暴力穷举法来解决TSP,需要尝试所有可能的城市排列,计算每个排列的路径长度,然后选择最短路径,其时间复杂度为 O ( n ! ) O(n!) O(n!),其中n是城市的数量。
这个很好理解,首次选择时有n个城市可选,第二次选择时从剩下的n-1个城市中选择,第三次选择时从剩下的n-2个城市中选择,以此类推,直到最后一次选择时就剩下1个城市。所以就是 n × ( n − 1 ) × ( n − 2 ) × . . . × 2 × 1 = n ! n\times(n-1)\times(n-2)\times...\times2\times1=n! n×(n−1)×(n−2)×...×2×1=n!。
动态规划
动态规划是一种用于解决TSP的有效方法,但它的时间复杂度也取决于问题的规模,其时间复杂度为 O ( n 2 ∗ 2 n ) O(n^2 * 2^n) O(n2∗2n),其中n是城市的数量,推导过程如下:
求解旅行商问题(Traveling Salesman Problem,TSP)的动态规划算法的时间复杂度取决于问题规模和算法的具体实现方式。TSP是一个NP-hard问题,因此不存在多项式时间复杂度的解决方案,但动态规划可以用来求解相对较小规模的TSP实例。下面是一个简单的TSP动态规划算法的时间复杂度分析:
假设有N个城市,我们要找到一条经过所有城市一次且回到起点的最短路径。
-
状态空间的大小:动态规划的核心是定义状态和状态转移方程。通常,我们可以使用一个二进制位向量来表示当前哪些城市已经访问过,例如,如果n=4,可以使用0001、0010、0100、1000来表示不同的状态,其中每个位代表一个城市是否被访问,所有这些状态构成了S。
-
状态转移方程:动态规划的关键在于状态之间的转移。对于TSP,状态转移方程通常是:
dp[S][i] = min(dp[S][i], dp[S-{i}][j] + dist[j][i])
d p [ S ] [ i ] dp[S][i] dp[S][i]表示从起始城市出发,经过集合S中的城市,最后到达城市i的最短路径长度。 d i s t [ j ] [ i ] dist[j][i] dist[j][i]表示城市j到城市i的距离。
- 时间复杂度分析:对于每个状态mask,需要遍历所有的城市i和找到一个城市j,因此状态转移的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。对于每个状态mask,都需要计算 d p [ m a s k ] [ i ] dp[mask][i] dp[mask][i],一共有 2 n 2^n 2n个状态(每个状态都对应一个mask),所以总的时间复杂度是 O ( n 2 ∗ 2 n ) O(n^2 * 2^n) O(n2∗2n)。
总之,TSP的动态规划算法的时间复杂度是指数级的,随着城市数量的增加,计算复杂度急剧增加,因此在实际应用中,通常需要考虑其他算法来处理大规模TSP实例。
P与NP关系:
P问题是NP问题的子集,也就是说,所有P问题都是NP问题。这是因为如果一个问题可以在多项式时间内解决,那么你也可以在多项式时间内验证解是否正确。但至今尚未知道P问题和NP问题是否相等,即P = NP或P ≠ NP。
如果P = NP,这意味着对于所有NP问题,都存在一个多项式时间的算法来解决它们,这将改变计算机科学和密码学的面貌,因为许多加密算法和安全协议都依赖于NP问题的难解性。但如果P ≠ NP,那么一些NP问题可能是非常难解的,这将保持当前的计算机科学理论和实际应用的基础。
总之,P和NP问题是计算机科学中复杂性理论的核心概念,它们关注了在多项式时间内解决问题的可行性和难度。这两个问题的解决与许多计算和优化问题的解决方式以及计算机科学的未来发展密切相关。
作业车间调度问题是典型的NP难问题
作业车间调度问题(Job Shop Scheduling Problem)被认为是一个NP难问题,这意味着它至少与NP问题一样难以求解。有几个原因解释了为什么作业车间调度问题被归类为NP难问题:
-
组合爆炸:在作业车间调度问题中,通常有多个作业(jobs)需要在一台或多台机器上执行,并且每个作业都有一系列的工序(operations)必须按照特定的顺序执行。这导致了组合爆炸,因为可能有许多不同的工序排列,每一种排列都需要评估其总执行时间。随着作业数量和机器数量的增加,问题的规模呈指数增长,这使得求解问题的所有可能解变得非常困难。
-
搜索空间巨大:对于作业车间调度问题,要找到最优解需要在所有可能的解中搜索,这个搜索空间通常非常大,因此暴力搜索所有可能的解是不现实的。这是NP难问题的一个典型特征,因为NP难问题的解决方案往往需要在庞大的搜索空间中进行搜索。
-
缺乏多项式时间算法:迄今为止,尚未发现一种能够在多项式时间内解决所有作业车间调度问题的算法。虽然有一些启发式方法和近似算法用于尝试找到接近最优解的解决方案,但对于大规模问题,这些算法也可能需要较长的计算时间。
咱们通过一个例子,直观地观察一下这种指数级的爆炸。
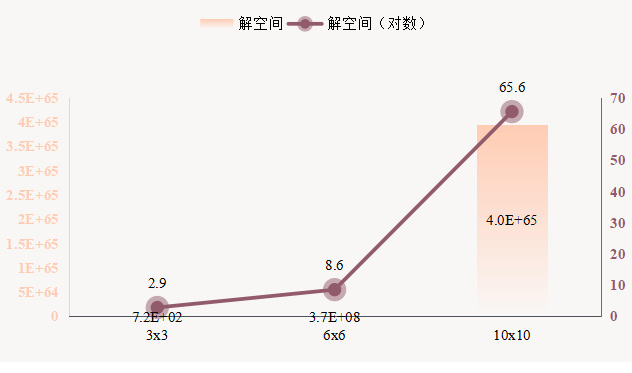
考虑一个3x3的JSP问题,即有3个工件和3台机器,每个工件各有3道工序恰好对应不同机器,那么每台机器均可加工3道工序,每台机器的不同工序排序数有3!=6种,那么3台机器就有3!x3!x3!=720种排序,看起来也不多。
接着考虑6x6的问题,排序数有 ( 6 ! ) 6 = 373248000 (6!)^6=373248000 (6!)6=373248000,一下子有点数不过来了,这也是我们为什么经常说6x6的问题人已经很难找到最优解了。
再看10x10的问题,排序数有 ( 10 ! ) 10 ≈ 4 × 1 0 65 (10!)^{10}≈4\times 10^{65} (10!)10≈4×1065,这会彻底蒙了!
如用完全枚举法,2022年排名世界第一的美国超级计算机Frontier运算速度达到每秒1.1百亿亿≈$1.1\times 10^{18} $次,那也需要 1.1 × 1 0 40 1.1\times 10^{40} 1.1×1040年,而地球年龄也仅为 45.5 亿年 ≈ 4.55 ∗ 1 0 9 45.5亿年≈4.55*10^9 45.5亿年≈4.55∗109年。
但是,如果仅仅是解空间大的问题,随着计算机速度的提升,终将也不是大问题。本质上在于,车间调度问题受制于很多要素的约束,比如日历、物料、夹具等,需要在众多解中寻找满足约束条件的解,而每个约束条件都会增加问题的复杂度,此时寻找一个可行解都比较困难。
综上所述,作业车间调度问题因其组合爆炸、庞大的搜索空间和缺乏多项式时间算法等特点,被认为是NP难问题。这意味着它属于那些尚未找到快速解决方法的复杂问题之一,通常需要使用近似算法来得到次优解,所以一种比较切合实际的方法就是,充分利用问题本身的特征,通过仿真的方式从大量数据中寻找次优解,建立特征与结果的映射关系,并固化为特定知识,从而在面对新问题时可快速匹配出合适策略。

![[GXYCTF2019]禁止套娃(特详解)](https://img-blog.csdnimg.cn/img_convert/421e0157dd09cbaf991338e1ea2cf210.png)