2024.1.29 GNSS 学习笔记

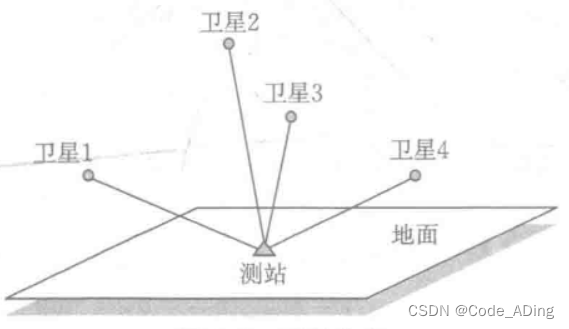
1.假设只对4颗卫星进行观测定位，卫星的截止高度角是15°，那么如何布设这四颗卫星的位置，使其围成的四面体的体积得到最大，以获得最好定位精度？

答：3颗卫星均匀分布在最低仰角面上，第4颗卫星在测站上空，此时4颗卫星所形成的体积最大，用户可以获得最好的定位精度。

2.为什么需要高精度时间？

授时的传统理解就是时间传递或者对时。比如以前手机没这么方便时，大家还都使用石英钟手表看时间时，大家都习惯晚上七点准时对着中央一套的报时，来校准你家的机械钟或者挂钟，这就是最简单的时间传递，这种时间传递的精度，秒的量级，对于日常生活已经足够。
但是全世界这么多表，如何将大家的时间都统一一起呢。以前的笨方法以及现在还在使用的方法就是，大家都把表放到一块，一块对比校准一下不就可以做到统一了嘛。但是全世界这么多设备，如何大家统一呢。像电视，就是时间传递的一种，其他的还有电话、电波授时等。

但是此类的授时，精度都相对较低，但有些场景我们又要比较高的时间精度。比如两个摄像头拍摄的画面，如果每个摄像头同1s内拍摄了10000张图片，如果我们要将两个设备拍摄的图像拼接起来，那么两个设备的时间相差要在1/10000秒以下，这样我们才能对⻬指定的画面。在我们传统的电力、移动通信等行业，有些时间的精度要在纳秒量级，也就是一亿分之一秒。

在分布式系统中，由于物理上的分散性，系统无法为彼此间相互独立的模块提供一个统一的全局时钟，而由各个进程或模块各自维护它们的本地时钟。由于这些本地时钟的计时速率、运行环境存在不一致性，因此即使所有本地时钟在某一时刻都被校准，一段时间后，这些本地时钟也会出现不一致。为了这些本地时钟再次达到相同的时间值，必须进行时间同步操作。授时技术又是实现时间同步的重要技术手段。

精密时间是科学研究、科学实验和工程技术诸方面的基本物理参量。它为一切动力学系统和时序过程的测量和定量研究提供了必不可少的时基坐标。精密授时在以通信、电力、控制等工业领域和国防领域有着广泛和重要的应用。现代武器实（试）验、战争需要它保障，智能化交通运输系统的建立和数字化地球的实现需要它支持。现代通信网和电力网建设也越来越增强了对精度时间和频率的依赖。从建立一个现代化国家的大系统工程总体考虑，导航定位和授时系统应该说是基础的基础。它对整体社会的支撑几乎是全方位的。

应用领域主要如下：

卫星发射
- 火箭发射升空后，不论是发射场、测控站以及测量船都会对火箭进行连续测控。而所有的测控都会根据火箭的⻜行轨迹和速度，推算出火箭将出现的方位和时间。这时候如果各个测控站的时间不同步，就有极大的可能追踪火箭失败。
航天活动
- 平常在电影中或者新闻里都会看到⻜船和目标⻜行器交会对接的画面。就像是我国“天舟一号”以及“天宫二号”的交会对接，都是需要精密的时间同步，对两个⻜行器进行姿态的同步观测，实时发出测控指令，才能保证对接成功，否则，“太空之吻”的美谈就很有可能变为“太空⻋祸”。
金融领域
- 现代金融行业，无论银行或证券交易所,都离不开计算机和计算机联网，单个计算机业务和计算机联网业务，如银行业务往来的发生时刻、金融交易的准确时刻、E-mail 信息和访问时间、数据库处理时间、银联卡/账戶的密码识别等等，都涉及银行联网计算机之间
  的时间同步和频率同步，都需要精准授时。
电力系统
- 对于电力系统而言，每一条由电厂汇入总干线的电流在同一时刻具有不同的相位。为让各电厂在每一时刻输送的电流按照预定的相位，而不至于发生在本该送入波峰而送入反向的波谷导致短路等情况，电网整体的工作协调需要一个全局统一的时钟完成。而电网的时钟同步正是由本文的标题，”GPS秒脉冲达成时间同步“来完成。

3.GNSS授时原理有哪些？

（1）卫星单向法

使用GNSS系统进行高精度授时的原理其实已经呼之欲出，我们前面提到的解算结果接收机钟差，其实就是本地时钟与GNSS时间框架的差异。
单向法的误差来源是卫星位置与星历的偏差、电离层层扰动以及接收设备误差等。能接收到多颗卫星信号，并进行⻓时间平均的十分理想的情况下，该方法可以达到接近1ns左右的时标同步精度。
一般来说，对已知精密坐标的固定用戶，观测1颗卫星，就可以实现精密的时间测量或者同步。若观测2颗卫星或者更多卫星，则提供了更多的观测量，提高了定时的稳健性。

（2）卫星共视法

两个地面站A和B同时观测一枚GNSS卫星，通过一定的同时观测时间安排，并通过网络传输进行对比，也可以实现授时。

（3）高精度时间传递 PPS

PPS：秒脉冲（Pulse Per Second）
形式化定义：GPS接收模块(GPS Receiver)可以产生秒脉冲信号，其作用是指示整秒的时间间隔，并通过PPS的上升沿标示GPS给出的UTC(Coordinated Universal Time)时间对应的具体时刻。其指示整秒时间精度可达数十纳秒级，无累积误差。每秒产生的该PPS与其给出的整秒时刻可以用于晶振精确调频⸺时钟同步。
GPS秒脉冲信号 pps 一秒钟一个，它的作用是用来指示整秒的时刻，而该时刻通常是用PPS秒脉冲的上升沿来标示。因为GPS可以给出UTC时间，但用戶收到时是会有延时的，那么为了精确授时，引入PPS信号上升沿来标示UTC的整秒时刻，精度可以到纳秒级，而且没有累积误差。

伪距差分定位原理站间单差

2.对同一个卫星同一频率的两个接收机观测值进行作差，即站间单差，可以完全消除卫星端的伪距硬件延迟误差以及卫星端钟差，如果两台接收机距离比较近(小于20km)，那么卫星信号的传播路径就十分相似，电离层和对流层延迟也会基本相等，所以可以适当减弱电离层和对流层的影响(可以减弱，但无法完全消除，有时可以看成0进行处理)：

3.单站几何距离公式是如何进行计算的？

4.两台接收机进行站间求差（对同一个卫星），求差后的几何距离是如何进行计算的？

通过站间单差后，轨道误差过小，可以忽略。

关于伪距差分定位原理方程构建

1.单个系统单个频率

2.单个系统多个频率

由于卫星端的码偏差已经通过站间单差消除掉，因此只需要再进行估计接收机端码偏差即可。

考虑接收机端码偏差并进行估计，扩展到单个系统多个频率，可以构建方程如下：

3.多个系统多个频率

上述是使用GPS单个系统的两种频率进行定位方程的构建，下面使用GPS+BDS两种不同的导航定位系统进行定位方程的构建：

当然，也可以选择BDS单独估计接收机钟误差，同时估计BDS第二频点相对于第一频点的码偏差。公式如下：

也可以选择每个频点估计一个接收机钟，公式如下：

4.为什么要使用码偏差作为参数进行估计呢？直接估计单个频点的接收机钟差不好吗？

只是码偏差随时间变化稳定，我们可以对其时间序列建立相关的随机模型，增加方程强度。简单来说就是上个历元的码偏差可以作为观测值给下个历元使用。

站星双差方程的构建

Kalman滤波

1.一个简单的小例子：

2.Kalman滤波算法公式：

利用kalman滤波公式，即可以计算当前历元的温度和精度信息。由此，就可以递推的计算后续的所有时刻的温度。（需要在每个历元有相应的观测值哟）

星间单差Kalman滤波伪距差分定位流程

使用星间单差的观测值形式，并使用kalman滤波的数据处理方法，实现伪距差分定位。

第一个是将kalman滤波应用到实际定位中，第二个是对接收机码偏差的随机过程进行建模，理解状态量的随机过程。

1.定位方程设置如下：

2.状态预测过程如下：

Q的意义：任何模型都有误差，为了防止预测的状态权重过大，增加过程噪声以降低后续加权平均中预测状态的影响，因此过程噪声的设置就构成了Q矩阵的构建。在程序中其实是找不到Q矩阵的具体设置的，通过对相关的参数在每一历元添加相应的过程噪声(随机游走)或者进行白噪声估计来处理协方差矩阵( Pk = P k-1 + （过程噪声)... )

动态模式下（速度、加速度）的状态转移矩阵。