349. 两个数组的交集

题目描述

给定两个数组 nums1 和 nums2 ，返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

示例 2：

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

提示：

• 1 <= nums1.length, nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 1000

数组解题

思路是使用两个辅助数组 a 和 b 来跟踪每个数组中哪些数字出现过。由于题目提示中给出的数字范围是 0 <= nums1[i], nums2[i] <= 1000，这两个数组的大小被设置为1000，对应可能存在的最大数字。

代码中的第一个for循环遍历数组 nums1，并在辅助数组 a 中对应的位置标记为1，表示这个数字出现过。同样的方法也应用于 nums2 和辅助数组 b。

之后，使用第三个for循环检查 a 和 b 中的每一个元素。如果两个数组在同一个索引位置上都标记了1，则意味着该数字在两个输入数组中都出现过，即它们的交集，因此将其添加到结果向量 nums3 中。

最终，nums3 包含了所有在两个输入数组中都出现过的唯一数字，即它们的交集，这个向量将被作为结果返回。

这段代码的理论执行时间复杂度为 O(n)，其中 n 是输入数组中元素个数的上限（这里是1000）。实际的时间复杂度取决于输入数组 nums1 和 nums2 的真实大小。空间复杂度是 O(m)，其中 m 是可能的数字范围的上限（在这个例子中是1000）。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        // 声明两个大小为1000的数组来记录两个输入数组中元素的存在情况
        // 初始化为0
        int a[1000] = {0}, b[1000] = {0};
        
        // 遍历第一个数组nums1
        for(int i = 0; i < nums1.size(); i++)
            // 将数组a对应位置标记为1，表示nums1中存在该元素
            a[nums1[i]] = 1;
        
        // 遍历第二个数组nums2
        for(int i = 0; i < nums2.size(); i++)
            // 将数组b对应位置标记为1，表示nums2中存在该元素
            b[nums2[i]] = 1;
        
        // 声明一个向量nums3，用于存储交集元素
        vector<int> nums3;
        
        // 遍历数组a和b
        for(int i = 0; i < 1000; i++) {
            // 如果某个元素在两个数组中都存在，则将其加入到nums3
            if(a[i] == 1 && b[i] == 1)
                nums3.push_back(i);
        }
        
        // 返回包含交集的向量
        return nums3;
    }
};

set容器解题

这道题目，主要要学会使用一种哈希数据结构：unordered_set，这个数据结构可以解决很多类似的问题。

注意题目特意说明：输出结果中的每个元素一定是唯一的，也就是说输出的结果的去重的， 同时可以不考虑输出结果的顺序

如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。
此时就要使用另一种结构体了，set ，关于set，C++ 给提供了如下三种可用的数据结构：

• std::set
• std::multiset
• std::unordered_set

std::set和std::multiset底层实现都是红黑树，std::unordered_set的底层实现是哈希表， 使用unordered_set 读写效率是最高的，并不需要对数据进行排序，而且还不要让数据重复，所以选择unordered_set。

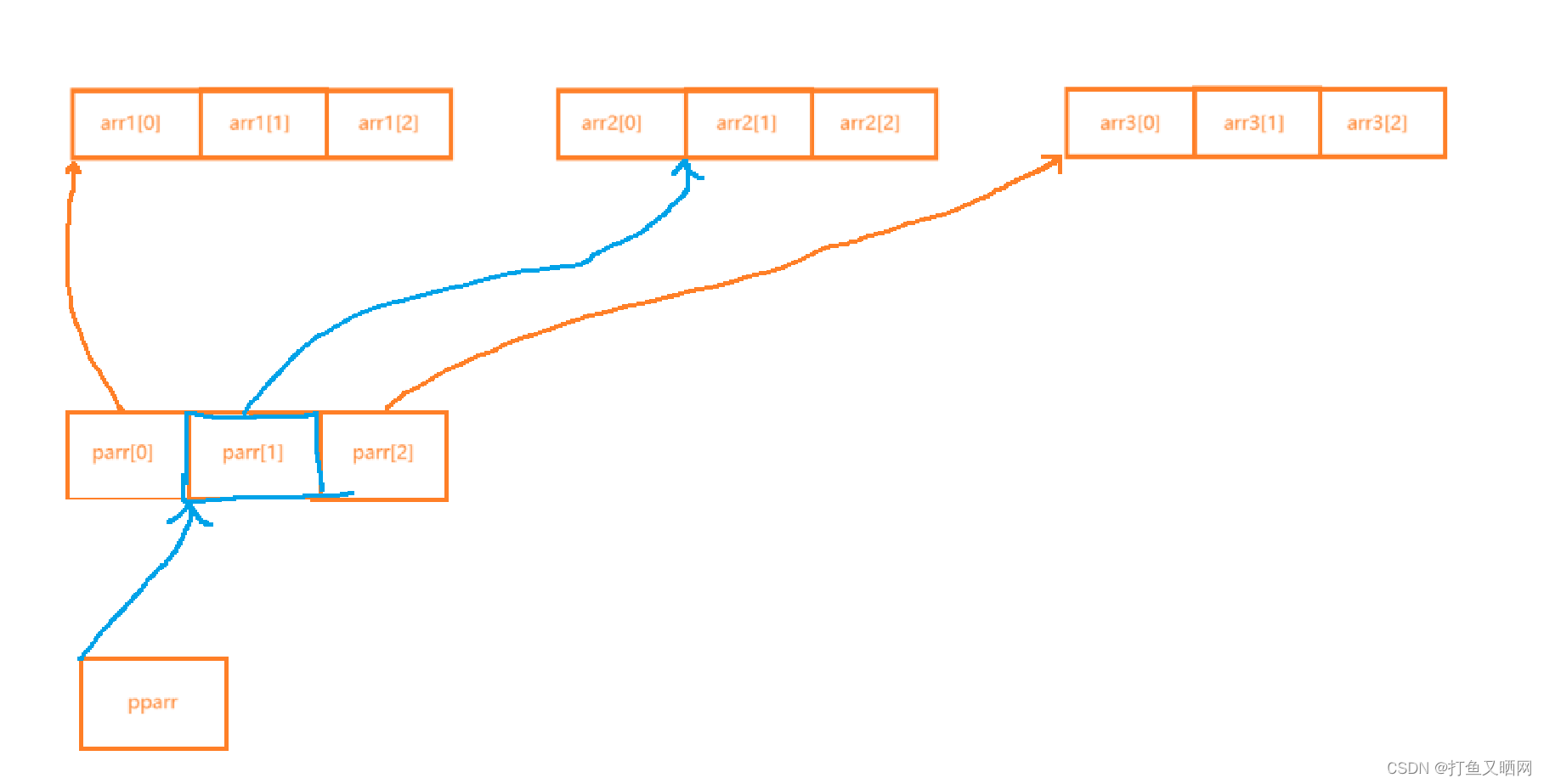
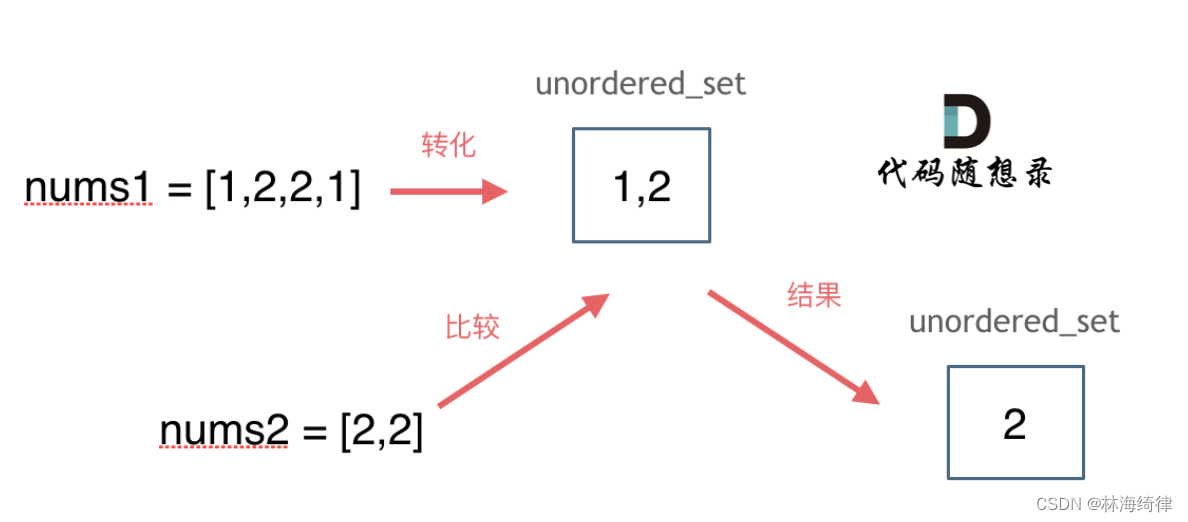
思路如图所示：

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        // 使用 unordered_set 来存储最终的交集结果，unordered_set 自动去重
        unordered_set<int> result;

        // 将 nums1 转换成 unordered_set，以便快速查找
        // 这里通过范围构造函数直接将 nums1 中的所有元素初始化到 set 中
        unordered_set<int> num(nums1.begin(), nums1.end());

        // 遍历 nums2
        for(int n : nums2) {
            // 使用 find 方法检查当前元素 n 是否存在于 nums1 的集合中
            // 如果存在，则说明 n 是 nums1 和 nums2 的交集中的一个
            if(num.find(n) != num.end())
                // 将 n 插入结果集合中，如果 n 已经存在，则不会重复插入
                result.insert(n);
        }

        // 将最终的交集结果转换成 vector 并返回
        // 这里也是通过范围构造函数，将 result 集合中的所有元素初始化到新的 vector 中
        return vector<int> (result.begin(), result.end());
    }
};

• set.find() ，返回给定值值得定位器，如果没找到则返回end()。

if(num.find(n) != num.end())//只要不等于end()就代表找到了

该思路数组版解题

代码的执行流程是这样的：

1. 声明一个 unordered_set result，用于存储交集，且自动去重。
2. 创建一个大小为 1000 的数组 a，用于标记 nums1 中出现的元素。这里假设元素值不会超过 1000，根据题目提示，这是一个安全的假设。
3. 遍历 nums1，对于 nums1 中的每个元素，将 a 数组对应索引处的值设置为 1。
4. 遍历 nums2，对于 nums2 中的每个元素，检查 a 数组中相同值的索引位置是否被标记为 1（也就是检查是否在 nums1 中出现过）。
5. 如果检查结果为 true（即 a[n] 等于 1），则将 n 添加到 result 集合中。
6. 最后，将 result 集合中的元素转换为 vector 并返回作为最终结果。
   由于 unordered_set 是基于哈希表的，因此插入和查找的平均时间复杂度是 O(1)。该算法的总体时间复杂度是 O(n + m)，其中 n 和 m 分别是 nums1 和 nums2 的长度。空间复杂度是 O(n)，其中 n 是两数组中不同元素的数量。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        // 创建一个 unordered_set 来存储交集的结果，自动去重保证元素唯一
        unordered_set<int> result;
        
        // 创建一个大小为1000的数组来记录元素是否存在于 nums1 中
        // 数组初始化为0，表示没有任何元素
        int a[1000] = {0};

        // 遍历 nums1，将存在的元素在数组 a 中对应位置标记为1
        for(int i = 0; i < nums1.size(); i++)
            a[nums1[i]] = 1;

        // 遍历 nums2
        for(int n : nums2) {
            // 如果当前元素在数组 a 中被标记为1（即出现在 nums1 中）
            // 则将其添加到结果集合中
            if(a[n] == 1)
                result.insert(n);
        }

        // 将 unordered_set 转换为 vector 并返回
        // 这里使用范围构造函数，将 result 中的所有元素初始化到新的 vector 中
        return vector<int>(result.begin(), result.end());
    }
};