它告诉我们什么？

直角三角形的三个边之间有什么关系。

为什么重要？

它提供了几何和代数之间的重要联系，使我们能够根据坐标计算距离。它也催生出了三角学。

它带来了什么？

测绘、导航，以及较近代出现的狭义和广义相对论——现有最好的关于空间、时间和重力的理论。

毕达哥拉斯定理的证明

古希腊人并没有将毕达哥拉斯定理表达为现代符号意义上的等式。那是随着代数的发展才出现的。在古代，该定理以口头和几何的方式表达。亚历山大里亚的欧几里得的著作记载了它最优雅的形式，这也是它的第一个文献证据。公元前250年左右，欧几里得写下了著名的《几何原本》——有史以来最具影响力的数学教科书，成为第一位现代数学家。欧几里得把几何学变成了逻辑：他明确地列出了自己的基本假设，并援引这些假设，为他的所有定理提供系统的证明。他建造了一座概念之塔，其基础是点、线和圆，而塔尖则恰好存在五种正多面体。

欧几里得几何“王冠上的明珠”就是我们现在所说的毕达哥拉斯定理：《几何原本》第一卷中的命题47。在托马斯·希思爵士(Sir Thomas Heath)的著名译本中，这个命题是这样写的：“在直角三角形中，直角所对的边上的正方形等于夹直角的边上的两个正方形。”(In right-angle triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.)

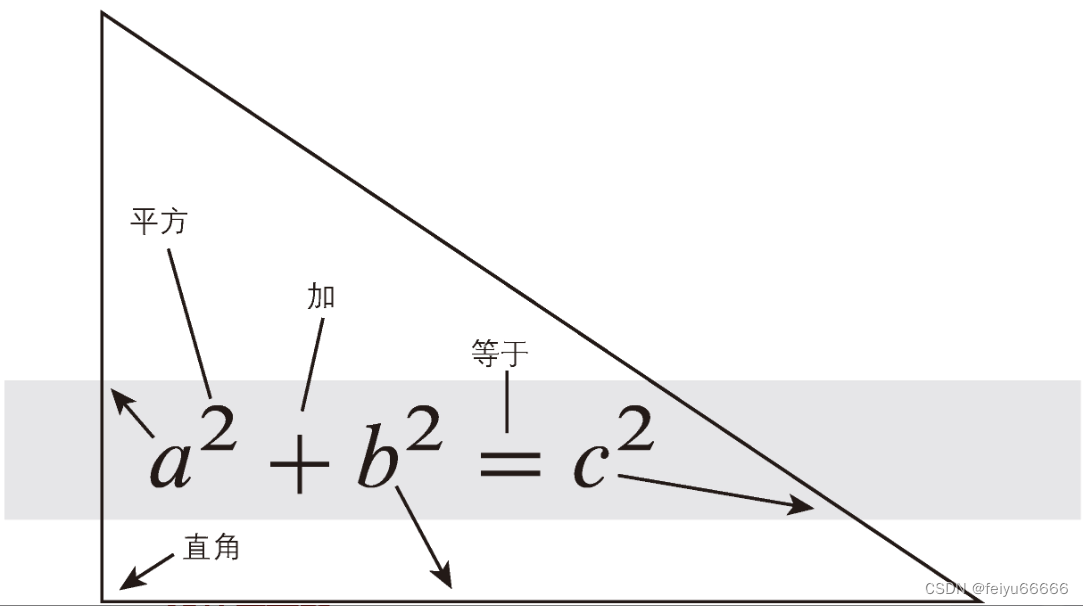
就高等数学而言，古希腊人使用的是直线和面积，而不是数字。所以毕达哥拉斯和他的古希腊后人将这个定理解释为面积相等：“用直角三角形中最长边构造的正方形面积，是由另外两边构造的正方形面积的和。”最长的一条边就是著名的“斜边”(hypotenuse)，意思是“在下面拉伸”。如果你以恰当的方向画图，确实如此，如图左所示。

欧几里得的证明相当复杂，它要在图上加上五条辅助线，如图左所示，还援引了几个先前证明的定理。维多利亚时代的男生（当时很少有女生学习几何学）不敬地称之为“毕达哥拉斯的裤子”。一个直接而直观的证明（虽然不是最优雅的）用了四个三角形来把同样一副数学拼图的两个解联系起来，如图1右所示。这张图确实很有说服力，但要把逻辑细节补充完整就得想一想了。比如：我们怎么知道图中的倾斜白色区域是正方形？

批注：书中并没有讲，我觉得中间那个其实是最好证明的，直角三角形的边长为a,b，中间的正方形边长为c，只要利用五个图形的面积和等于大正方形的面积就可以推导出勾股定理了。

毕达哥拉斯定理的应用

我们在现实生活中遇到的许多三角形都不是直角三角形，因此方程的直接应用似乎有限。但是，任何三角形都可以分割成两个直角三角形，而任何多边形都可以分割成若干三角形。因此，直角三角形是关键：它们证明了三角形的形状与其边的长度之间存在有用的关系。从这一见解中发展出来的学科是三角学——“三角形的测量”。

……

毕达哥拉斯定理本身很重要，但它的推广能发挥更大的影响力。这里我就只谈谈这些后期进展中的一项，来揭示与相对论之间的联系，我们将在第13章中进一步介绍。

黎曼几何

高斯的贡献

欧几里得从不多的几个基本假设中得出了他的所有定理，他将其归类为定义、公理和一般概念。他的体系优雅、直观、简洁，只有一个明显的例外，就是他的第五个公理：“若两条直线都与第三条直线相交，并且在同一边的内角之和小于两个直角，则这两条直线若无限延长，必定在这一边相交。”

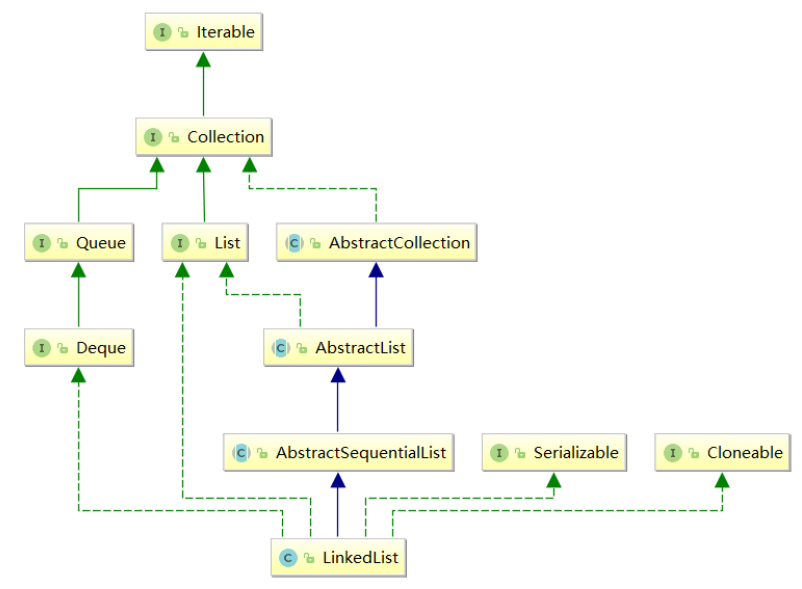
一千多年来，数学家们试图修复他们眼中的缺陷。他们不只是在寻找更简单、更直观的东西来达到同样的目的（虽然有几个人找到了这样的东西），他们想证明这条尴尬的公理来彻底摆脱它。经过了几个世纪，数学家终于意识到存在另一种“非欧氏”几何，这也就意味着证明根本不存在。这些新的几何与欧氏几何一样逻辑自洽，遵循了除了平行公理之外的所有公理。它们可以被解释为曲面上的测地线（最短路径）的形状，如下图所示。这引起了人们对曲率意义的关注。

欧氏平面是平的，曲率为零。球面在任何地方的曲率都相同，并且是正的：它在任何点附近都看起来像一个圆顶。（一些技术细节：大圆会在两点上相交，而不是像欧氏公理要求的一点，因此球面上的几何对此做了修正——找到对径点，并认为它们是同一点。这样一来球面就变成了所谓的射影平面，这种几何称为椭圆几何。）还存在恒定负曲率的表面：在任何点附近看起来都像马鞍。这种曲面称为双曲平面，它可以用几种很乏味的方式来表示。最简单的方法也许是将其视为圆盘的内部，并将“直线”定义为与圆盘的边缘垂直相交的圆弧

也许你会觉得，虽然平面几何可能是非欧的，但对于空间几何来说肯定行不通。你可以把平面弯折变成三维的，但是你没办法弯折空间，因为再没有额外的维度了。然而，这种想法相当幼稚。比如，我们可以使用球体的内部来模拟三维双曲空间。直线可以用与边界垂直相交的圆弧来表达，而平面就可以用与边界垂直相交的球面的一部分来表达。这种几何是三维的，满足欧氏几何除第五公理外的所有公理，并且从确定意义上定义了一个弯曲的三维空间。但它并不是围绕着任何东西弯曲的，也没有弯向任何新的方向。

它就是弯曲的。

有了这些新的几何，一种新观点开始占据舞台中心——然而它是物理的，不是数学的。既然空间不一定是欧氏的，那它到底是什么形状的呢？

我说三维双曲空间“就是弯曲的”，是基于一个关于曲率的新观点，它也可以追溯到高斯。球面有常数正曲率，双曲平面有常数负曲率。但是一个曲面的曲率不一定是恒定的。它可能在某些地方弯折得厉害，在其他地方则不那么厉害。实际上，它的曲率可能在一个地方是正的，在另一个地方是负的。曲率可以在不同地方之间连续变化。如果一个曲面看起来像是狗啃的骨头，那么两头凸起的地方是正曲率的，但是连接部分则是负曲率的。

高斯想要找到一个公式来表达任何点的曲面曲率。当他最终找到它，并于1828年将其发表在《关于曲面的一般研究》(Disquisitiones Generales Circa Superficies Curva)一书中时，他将其命名为“绝妙定理”。绝妙在哪里呢？高斯从朴素的曲率观点着手：将曲面嵌入三维空间并计算它的弯曲程度。但答案告诉他，周围的空间并不重要。它没有出现在公式中。他写道：“公式……引出了一个非凡的定理：如果在任何其他曲面上形成一个曲面，则每个点的曲率度量保持不变。”他所说的“形成”意思是“包裹”。

拿一张平整的纸，其曲率为零。现在将它包在一个瓶子上。如果瓶子是圆柱形的，则纸张完全贴合，不发生折叠、拉伸或撕裂。就外观而言，它是弯曲的，但这是一种微不足道的弯曲，因为它没有以任何方式改变纸张上的几何形状。它只是改变了纸张与周围空间的关系。在平面的纸上画一个直角三角形，测量它的边，用毕达哥拉斯定理检验。现在将这张图包裹在瓶子上。沿纸张测量的边长不会改变。毕达哥拉斯定理仍然成立。

然而，球体的表面具有非零曲率。因此，无法用一张纸包裹并紧贴球体，而不发生折叠、拉伸或撕裂。球面几何与平面几何有本质的区别。例如，地球的赤道，以及0°和90°的经线确定了一个三角形，它有三个直角和三条等长的边（假设地球是一个球体）。所以毕达哥拉斯方程就不成立了。

今天我们把本质意义上的曲率称为“高斯曲率”。高斯用了一个迄今仍不过时的生动类比来解释它为什么重要。想象一下，一只蚂蚁被限制在一个表面上。它如何知道表面是不是弯曲的呢？它无法走出表面来看看它看起来弯不弯。但它可以使用高斯公式，通过纯粹在表面内进行适当的测量来确定。当试图找出所在空间的真实几何时，我们也处在和蚂蚁相同的处境——无法走出空间。然而，在通过测量来模拟蚂蚁之前，我们需要一个三维空间的曲率公式。高斯并没有给出一个这样的公式，但他的一个学生，在鲁莽冲动的驱使下，声称自己做到了。

黎曼流形

1854年，黎曼发表了他的演讲，受到了热烈的欢迎。这也难怪。他定义了一个所谓的“流形”(manifold)，意思是“多重折叠”(many-foldedness)。从形式上看，“流形”由一套有许多坐标的坐标系，以及计算附近点之间距离的公式（现在称为黎曼度量）确定。不那么正式地说，流形就是一个非常壮观的多维空间。黎曼演讲的高潮是一个推广了高斯绝妙定理的公式：它仅根据度量来定义流形的曲率。正是在这里，这个故事就像衔尾蛇一样形成了完整的闭环，吞下自己的尾巴：因为在这个度量中可以看到毕达哥拉斯的痕迹。

比方说有一个流形是三维的。设一点的坐标为(x,y,z)，(x+dx,y+dy,z+dz)为附近一点,如果空间是欧氏空间，曲率为零，则这两个点之间的距离ds满足方程:，这就是毕达哥拉斯定理，仅限于附近的点。如果空间是弯曲的，点到点的曲率可变，则类似的公式（也就是度量）如下所示：

,这里的X、Y、Z、U、V、W可以取决于x、y、z。它可能看起来有点儿绕，但就像毕达哥拉斯方程一样，它讲的是平方和（以及密切相关的两个量的积，如dxdy）再加上几个点缀。出现2倍是因为这个公式可以表达为[插图]的表（矩阵）：

其中X、Y、Z各出现一次，但U、V、W出现了两次。这张表是沿对角线对称的；用微分几何的语言来说，它是一个对称张量。黎曼对高斯绝妙定理的推广就是用这个张量来表达的任何一点上的流形曲率公式。在适用毕达哥拉斯定理的特殊情况下，曲率变为零。所以通过检验毕达哥拉斯方程是否成立，就可以检验曲率是否存在。

与高斯公式一样，黎曼的曲率表达式仅取决于流形的度量。被限制在流形上的蚂蚁可以通过测量微小的三角形并计算曲率来观察度量。曲率是流形的固有性质，与周围空间无关。实际上，度量已经确定了几何，而不需要周围空间了。特别是我们这些人类“蚂蚁”可以问问庞大而神秘的宇宙是什么形状，并希望通过一些不需要走出宇宙就能进行的观察来回答这个问题——因为我们也走不出去。

黎曼利用力来定义几何，找到了他的公式。五十年后，爱因斯坦将黎曼的思想翻转过来，用几何来定义他的广义相对论中的引力，并启发了关于宇宙形状的新思想（见第13章）。这一连串发现过程堪称惊人。毕达哥拉斯方程首次出现在3500年前，用于测量农民的土地。它拓展到非直角三角形和球面三角，让我们能够绘制大陆的地图并测量我们的星球。接下来一个杰出的推广让我们得以测量宇宙的形状。重要的思想来自小小的发端。