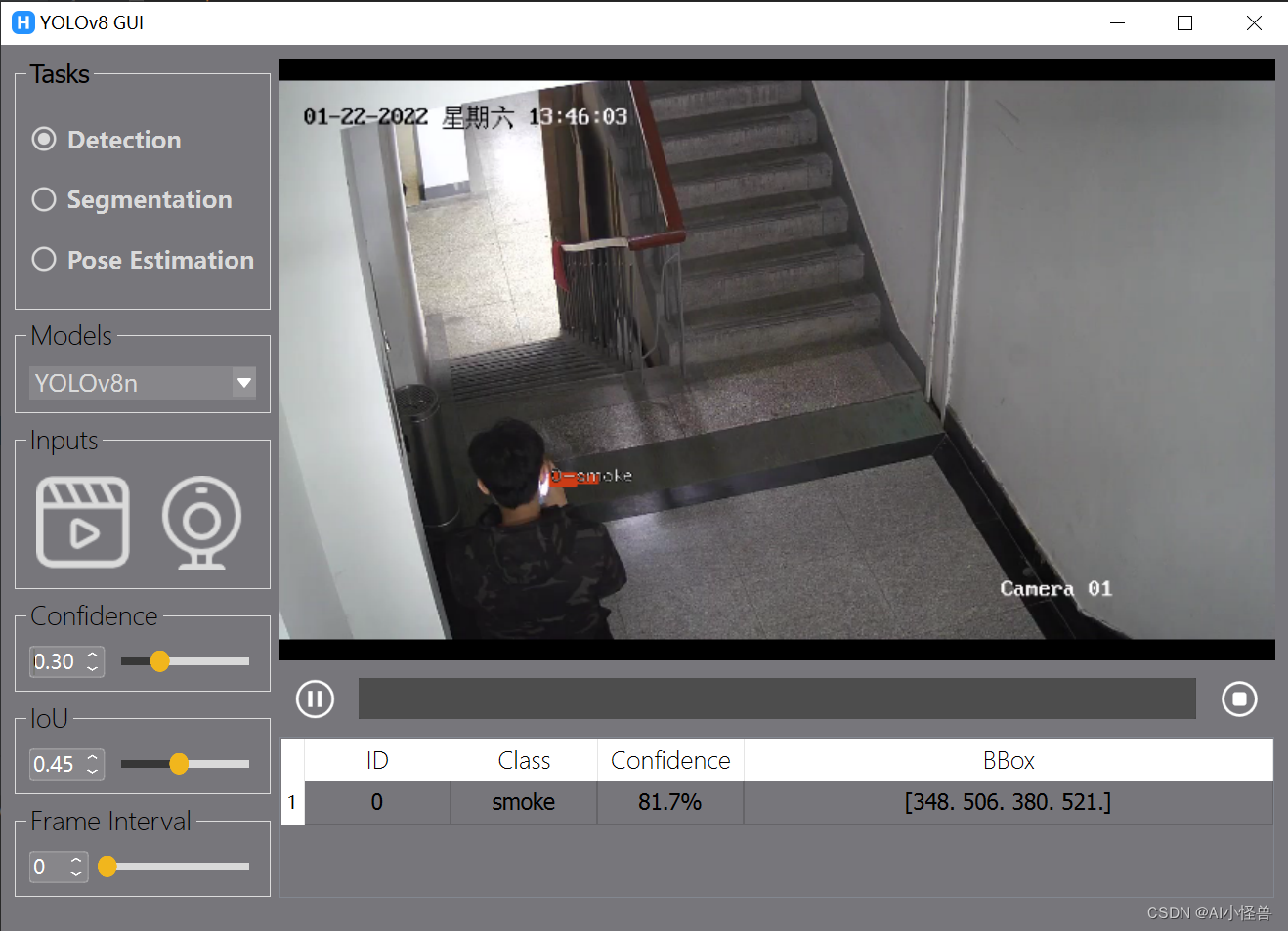
卷积神经网络简称为CNN
首先我们来回顾一下,我们之前学到的全连接的神经网络:
上面我们通过线性层串行连接起来的神经网络,我们叫做全链接的网络,在线性层里面,我们的输入值和任意的输出值之间都存在权重,也就是说我们的每一个输入节点都要参与到下一层的输出节点的计算上面,因此我们称这样的线性层叫做全连接层(任意两层之间所有的节点都进行连接)。
下面我们介绍二维卷积的神经网络:
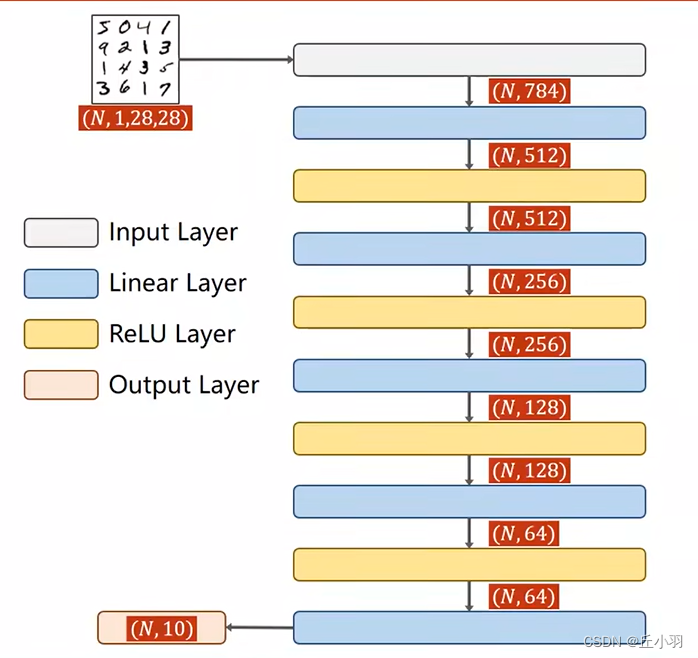
例如我们的手写图像识别,我们输入的是一个1*28*28的张量,这三个值分别是channel(通道数),width(宽度),height(高度)。然后我们这个图像要通过卷积层处理得到4*24*24。
为什么不直接使用全链接层呢?(全连接层需要将输入转化为一个向量,向量是一长段的数,不具有空间上的二维特征,不能很好的保留输入之间层与层之间的联系,但是我们图像层与层之间的信息我们还是要保留的,所以我们通过使用卷积,将其转化为具有空间结构的张量,明显全链接的运算只有矩阵运算,维度最高才是二维,包含层级之间的信息比较少)。
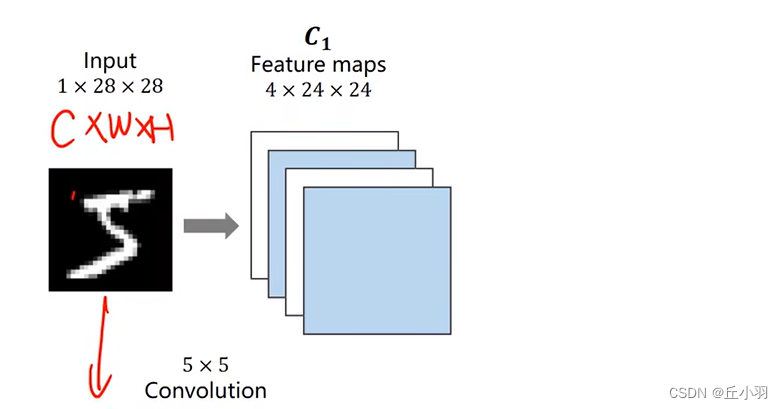
我们希望保留图像的空间信息,通过卷积,我们将其转化为四个通道,24*24的像素。(当然也是CWH,通道和长度高度都有可能改变)。显然,一个图像经过卷积层卷积出来的结果仍然是一个三维的张量,接下来我们做一个2*2的下采样。
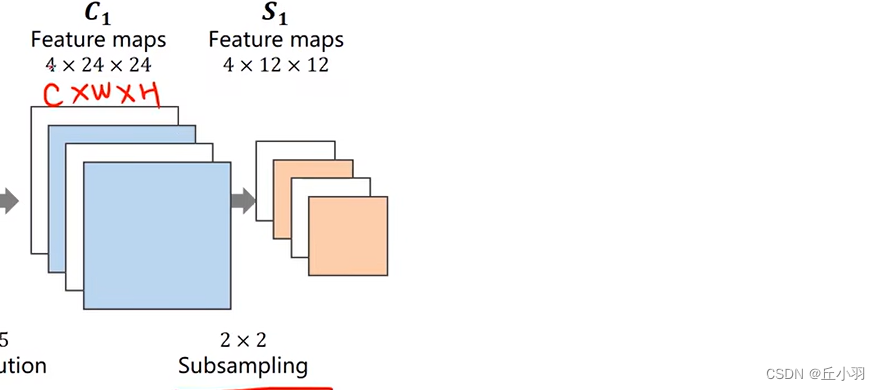
经过下采样处理之后,我们的输出就变成了4个通道,12*12的像素。在采用下采样的过程中,我们的通道数是不变的,但是图像的宽度和高度会发生改变,下采样的作用是减少我们数据的数据量,减少元素数量,降低计算需求。最终的目标是要做分类,所以不管我们中间层怎么处理,我们的输出都要是一个十维的向量,即10*1的矩阵。那我们就需要采用一些方法:比如先升高,再降低。不管我们使用什么方法,我们最终一定是将1*28*28的三维输入,转化为一个10*1的二维输出(也可以叫做是长度为10的向量)。
事实上我们将其转化的过程如下图:
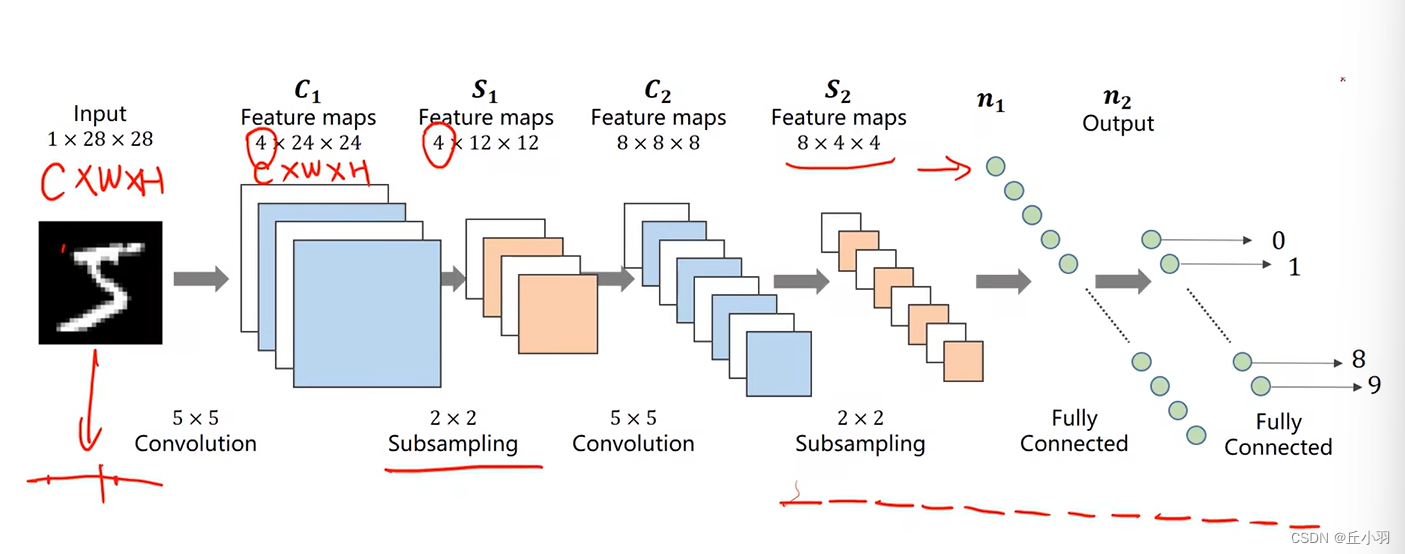
我们从三阶张量输出一个向量。怎么实现维度转化呢?我们以S2到n1为例,我们将平面沿着通道数展开,就将8*4*4转化为了32*4(即将每个通道里的张量放在同一纬度一次排开)。得到n1,我们再使用全连接层,将其映射到十维的输出。然后我们再接上交叉熵损失,用SoftMax去计算它的分布,最终呢,我们就可以去解决分类问题。那我们在构建神经网络的时候,首先要明确,我们的输入,它的张量的维度,输出的张量的维度,我们要想使我们的网络正常的工作,我们就需要利用我们网络的各种层,进行维度上或者每个维度上尺寸大小的变化,最终使其映射到我们想要的各种输出里面,所以不论是卷积也好,全链接也好,我们都是在做空间变换,所以我们在神经网络里面,前面的卷积也好,下采样也好,其实我们都可以称其为Feature Extraction(特征提取)。
我们能通过卷积运算,找到他们的某种特征,全链接的网络叫做分类器。
讨论卷积之前,我们首先来讨论图像:

明显,这个图像是一只猫,在计算机里面,我们会将图像分割成一个个格子,每个格子都有颜色值,我们将每个格子的颜色都填上去,就构成了图像,这样我们就构成了图像,这叫做栅格图像,从自然界获取图像的手段一般都是栅格图像,不管是用手机,用摄像机,我们获取的图像都是栅格图像。
除了栅格图像还有一种图像叫做矢量图像,矢量图像不是可以从自然界直接捕获的,而是需要人工生成,或者称之为程序生成的。我们描述矢量图像的时候,不是使用图像的方式,而是描述他的特征,例如用计算机做出一个圆,我们描述它的圆心在哪,直径是多少,边是什么颜色,填充什么颜色。简单的例子就是easyx。
我们拿到一个图像肯定是分成红绿蓝三个通道,也就是我们常说的channel,这个在深度学习里面,我们将默认输入图像的RGB,我们称之为Input Channel。
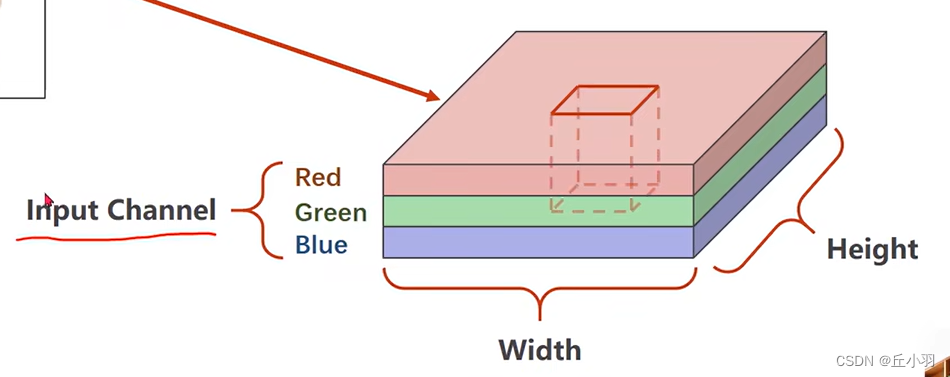
如果我们在这个图像中取一个小块。

我们使我们的块在图像上依次开始滑动,用块儿的大小,将图像遍历一遍,然后对每一个块儿都进行卷积运算,最后得到输出卷积结果,将输出卷积结果放到一起。
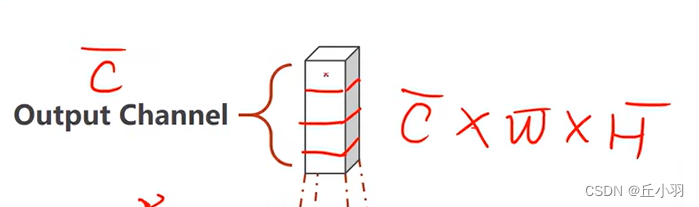
我们得到的块儿的通道数,宽度和高度都有可能改变,例如图中通道数从3变成4,可能是由下面三层进行相加得到的结果作为第四层。当然包含了原有信息,而且又能增加一个新的信息。新的信息获得新的特征。
下面我们来看卷积的运算过程:
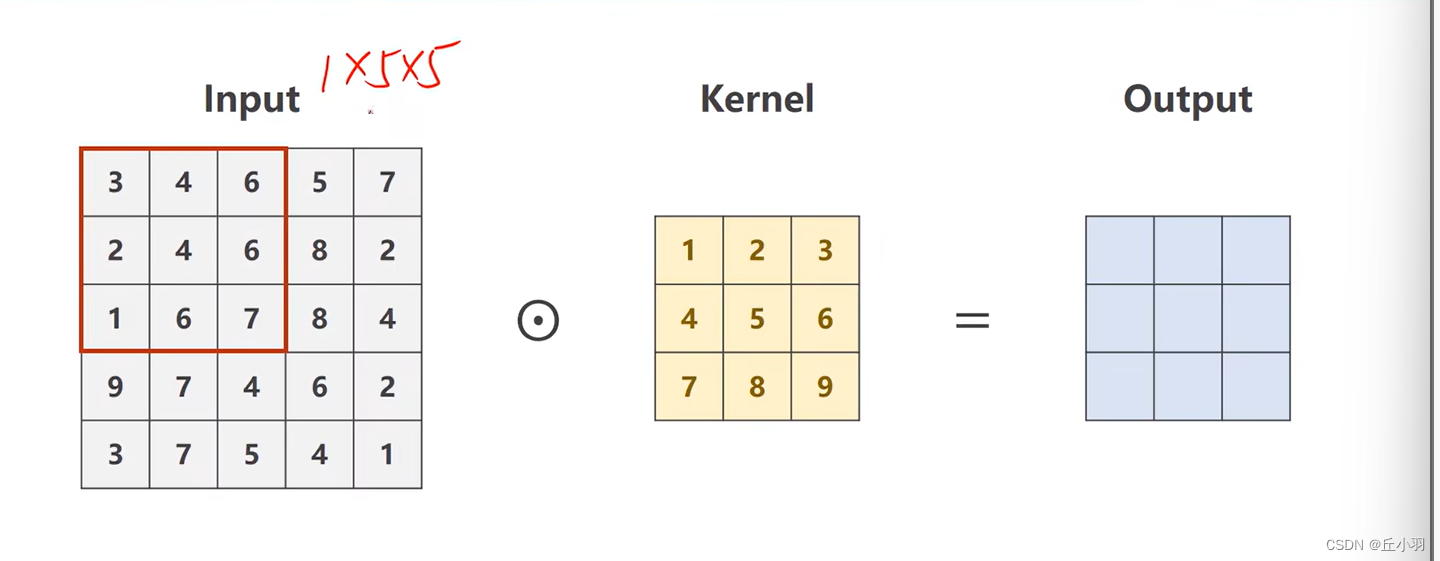
假设我们刚开始的输入是一个1*5*5的张量,卷积核是1*3*3的张量。我们要先用3*3的核在输入里面画出一个3*3的窗口,就是输入里面的红圈部分,然后使红圈里面的数据和我们卷积核里面的数据做数乘。
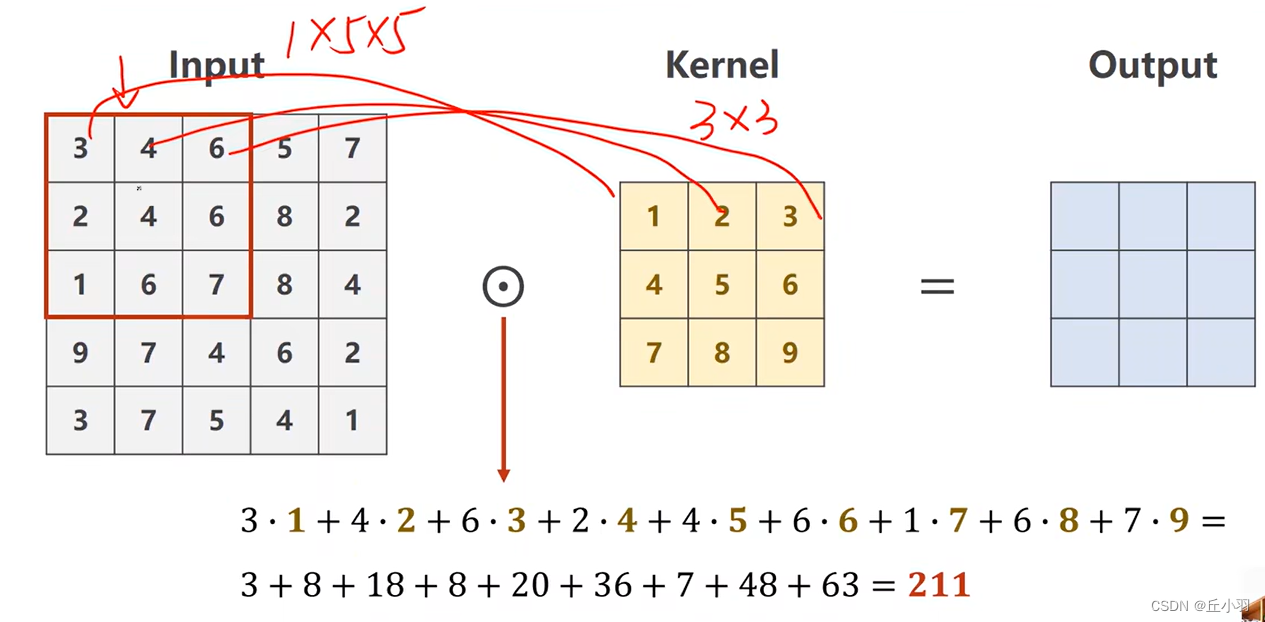
得到的结果作为我们输出的元素,同理,我们将块儿往右边移动(也就是逐渐进行遍历)。做同样的运算,得到的结果作为输出的元素。写入output。
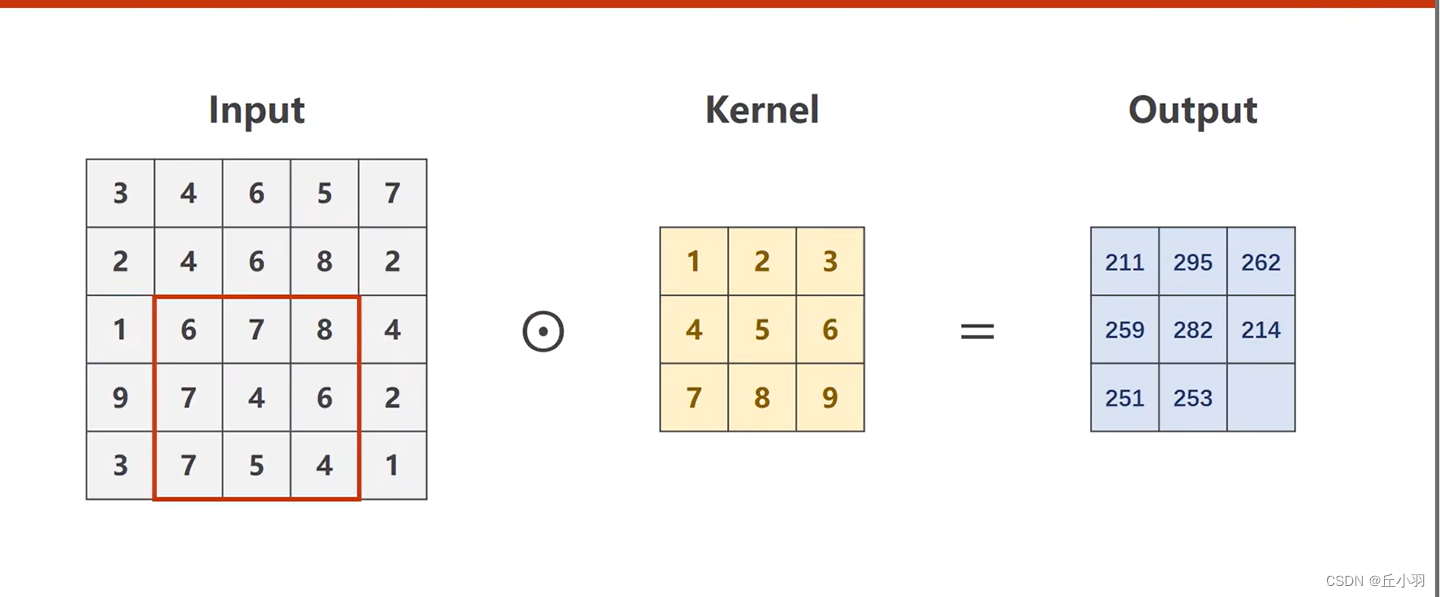
直到全部遍历完成得到输出,注意:这是单通道,也可以说成是矩阵的卷积,但是我们经常做卷积的输入是多通道。三通道用的比较多,但是有时候也会有上百个或者更多的通道。
我们以三个通道为例:
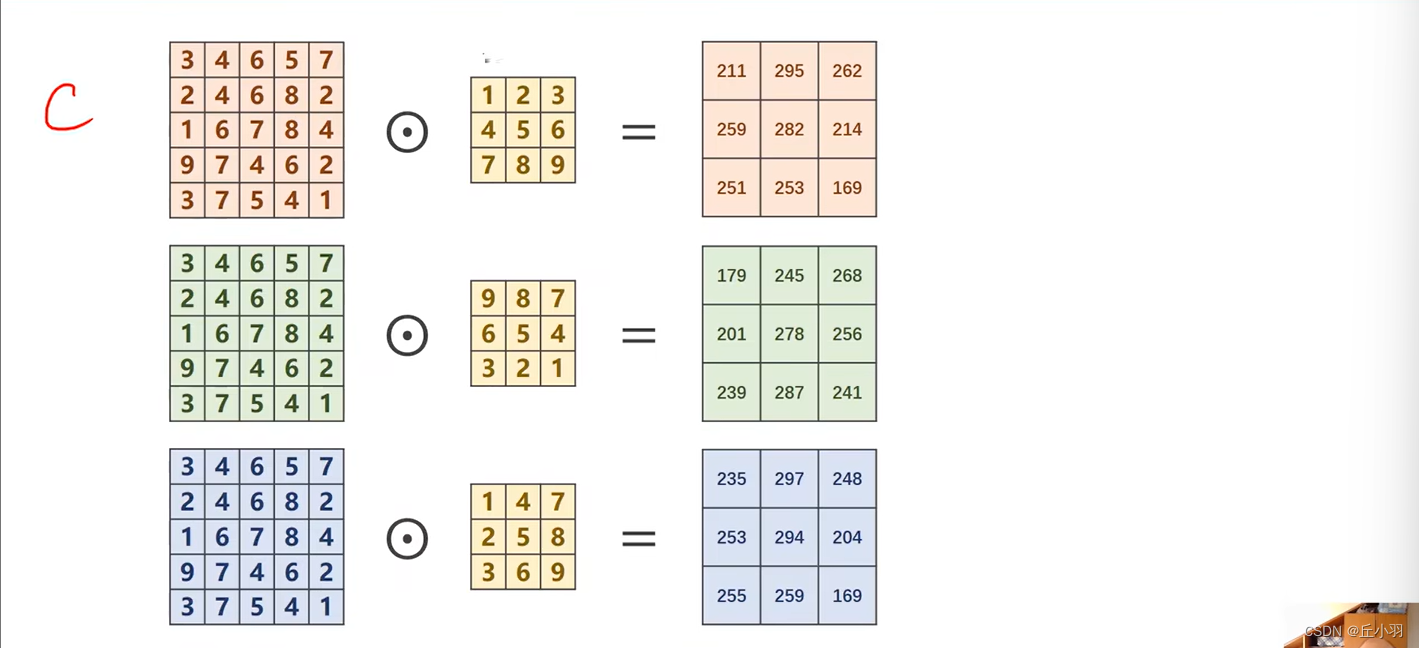
我们对于每个通道都要进行卷积,每个通道对应一个卷积核,那么有多少个通道,我们就需要有多少个卷积核。如果我们输入的通道有五个,那么我们需要五个卷积核。
接下来我们需要对三个矩阵做加法,得到一个通道:
那我们就是3*5*5的输入和3*3*3的卷积核进行相乘(这就叫做卷积运算)。得到一个1*3*3的通道。
那么显然,在这种情况下,我们的输入的通道有三个,但是输出的通道数只有1个。
显然,我们对于3*3的卷积核,我们的输出结果的长和宽对应输入是要分别减去2的。
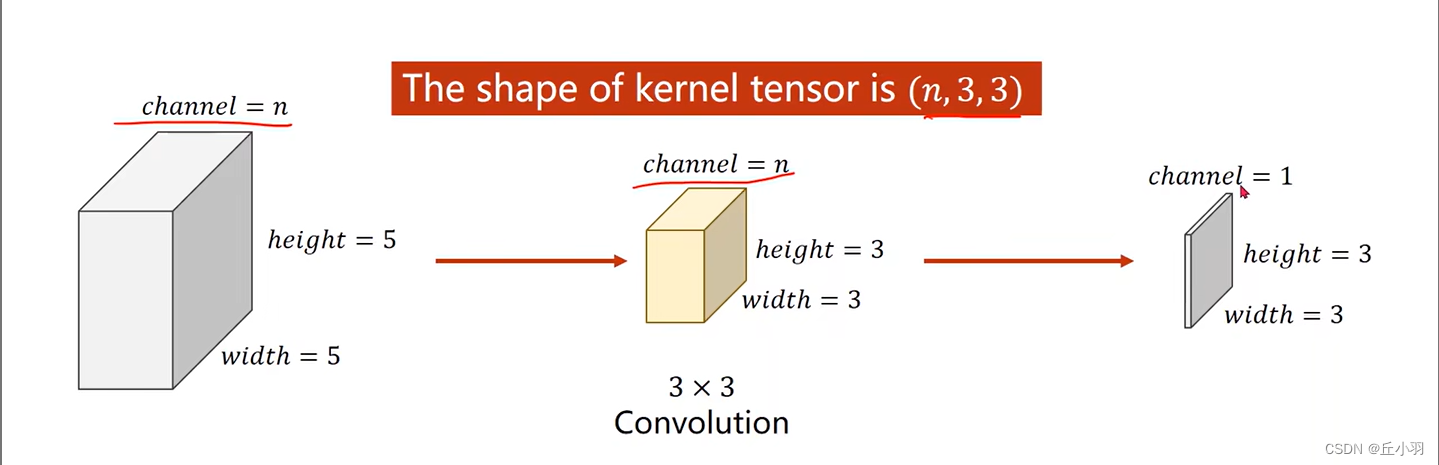
显然,我们经过n*3*3的卷积核,我们的输出是一个通道,但是,如果我们能使用多个卷积核,我们就能得到多个通道,这些通道按层次叠起,就得到一个多通道的输出。
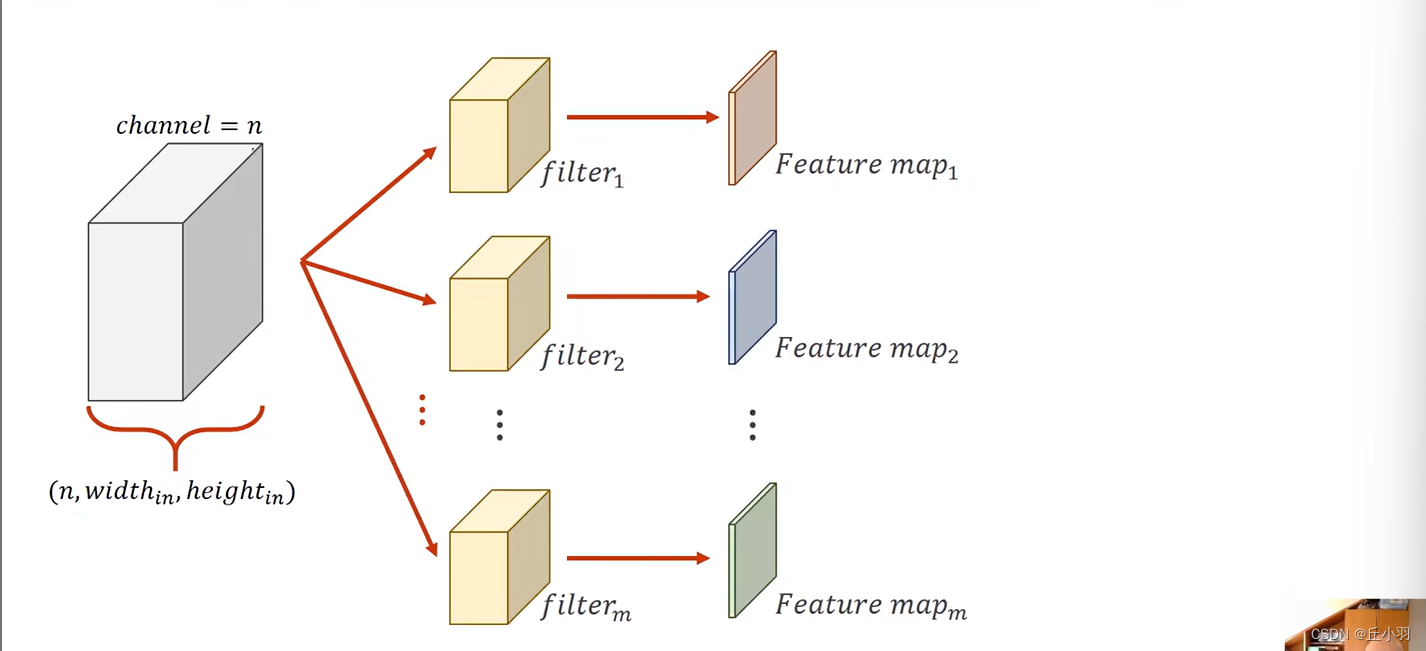
然后我们将通道按顺序叠起:
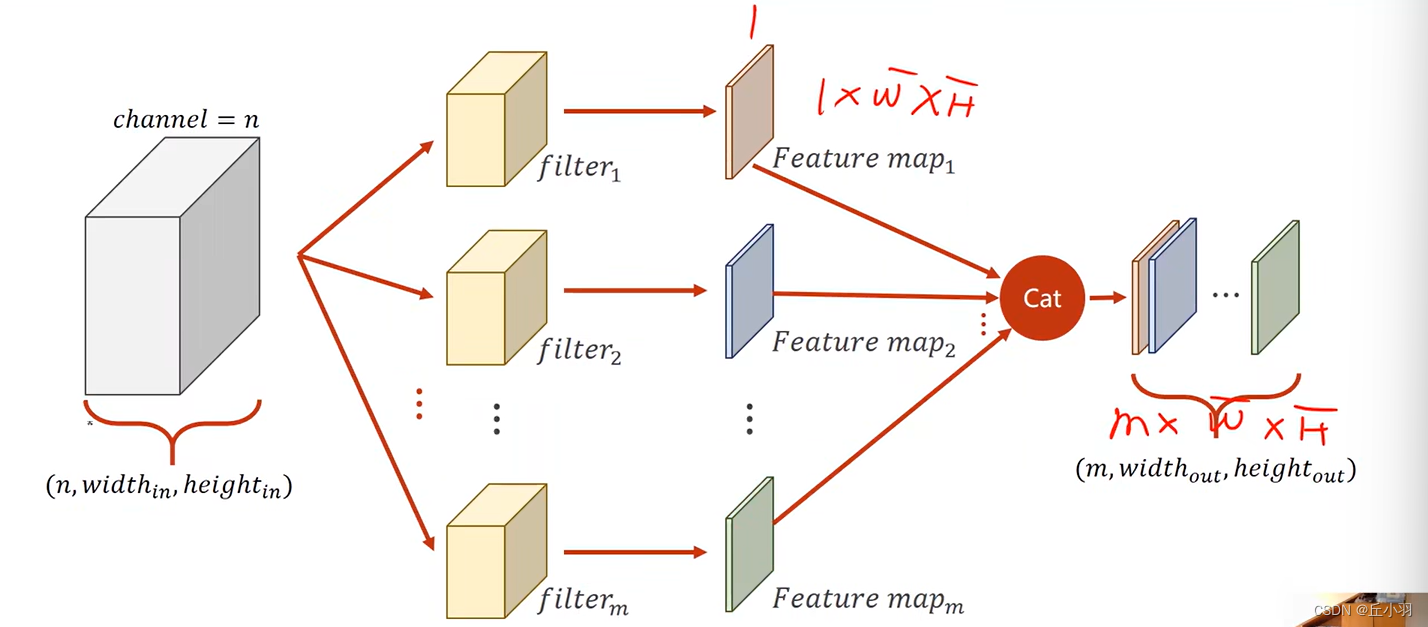
由上面的图,我们有以下几个发现:
1,每个卷积核的通道数量要求和输入的通道数量是一样的。
2,这种卷积核的总数要求和输出的通道数量是一样的。
3,卷积核的长和宽是自定义的。
所以我们就可以由输入层和输出层来判断卷积核的维度:

卷积层中卷积核的个数由输出维度决定,每个卷积核中有多少层由输入维度决定。
下面是我们在pytorch中实现的代码分析:

这里的batch_size表示的是输入的个数,卷积核的参数:输入维度,输出维度,卷积核的形状,形状一般表示是正方形,当然,我们也可以表示为长方形。
接下来,我们把我们的输入传给卷积层进行处理得到output输出。

接下来我们来看上面张量形状的输出:符合我们的预期。
当然,我们对于卷积层的形状来说,后面两个参数,宽度和高度是可以我们自己定义的,前面两个参数是要根据输入的形状和输出的形状来决定。

有时候我们希望输入的维度是5,输出的维度也是4,在不改变卷积层的形状的同时,我们需要对输入进行处理,将其扩大一圈(或者多圈),扩大的部分的元素全部填为0,然后再经过卷积层处理,得到我们的结果。 当然,默认是填充0,但是还有很多种选择:

下采样:
我们用到的比较多的下采样方法是最大池化层(MaxPolling),我们要怎么做呢?
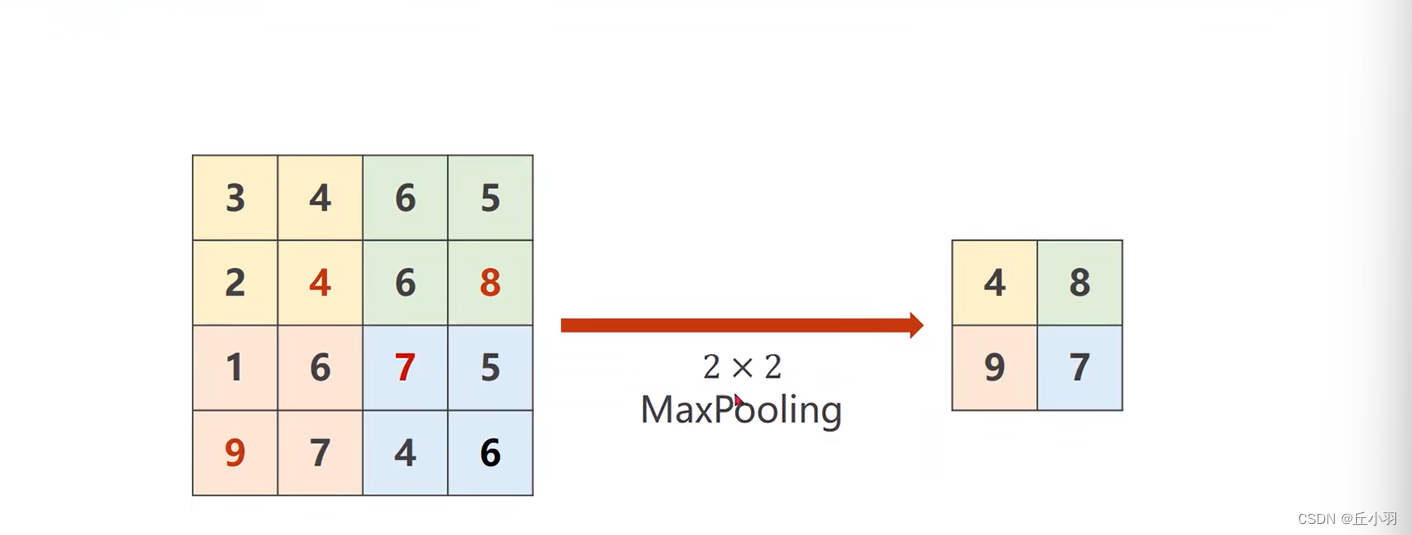
以上图为例,最大池化层是没有权重的(前面我们学的那些层,卷积层,全连接层都是带有权重的),2*2的最大池化层它的工作原理是什么样的呢?我们可以把4*4的图像分成2*2一组,然后在每一组中找最大值,然后将最大值拼成2*2的矩阵,作为新的一组输出。
很明显,我们在做最大池化的过程中,我们只是对每个通道进行最大池化,通道之间不能进行最大池化操作的,显然,上图中输入的是一个通道的数据。所以做池化,或者说下采样,通道数量是不改变的,但是形状(指的是宽和高是会改变的)。例如我们使用2*2的池化层,我们的图像大小会缩小到原来的一半,同理,3*3会缩小1/3。
下面我们来具体实现:

首先我们进行卷积处理,我们的卷积层:面积(指的是长*宽)5*5,输入通道是1,输出通道是10。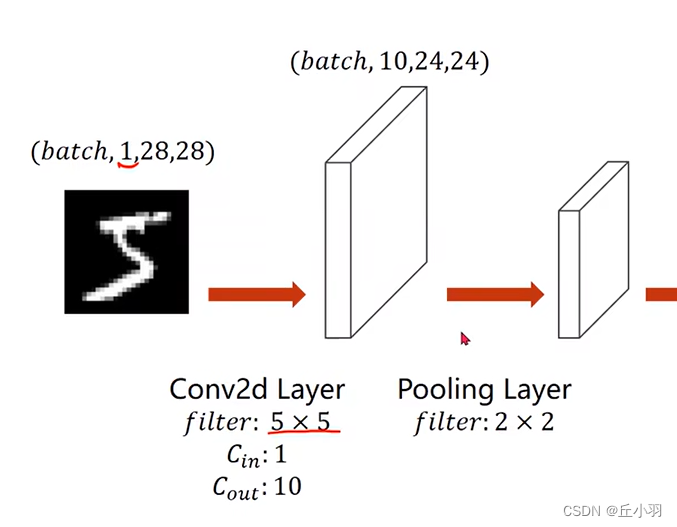
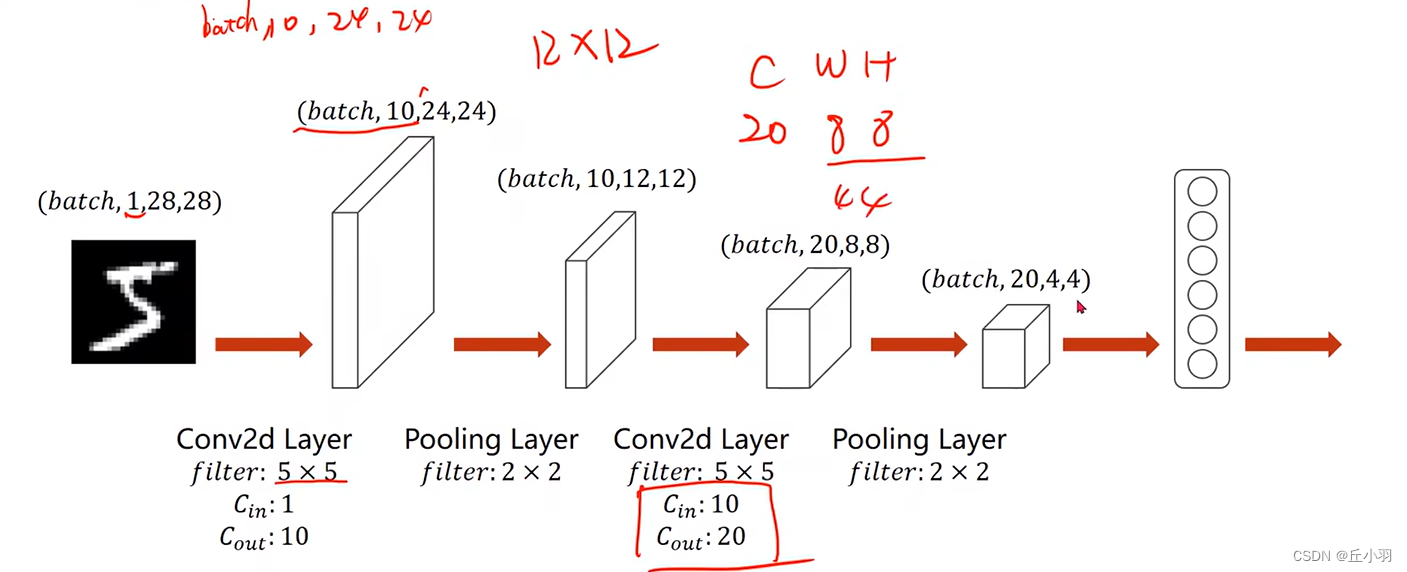
经过卷积之后,我们还要做一个最大池化,得到一个10*12*12的张量,然后我们再使用一个5*5的卷积核,输入通道和输出通道分别是10和20,得到的输出是20*8*8,最后再做一个池化层,得到20*4*4的张量。
那么现在,我们得到320个元素,然后这320个元素,我们将其转化为一个向量,然后经过全链接层,输出的向量元素个数是10。
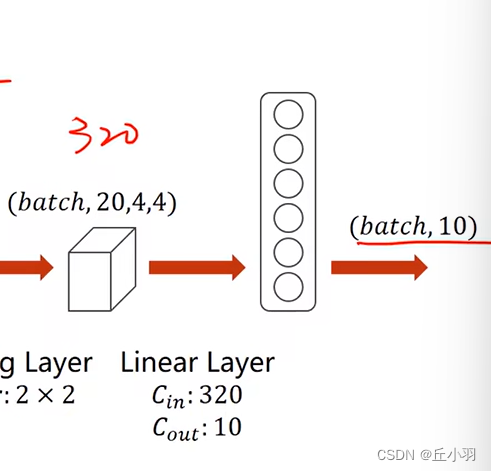
卷积层和池化层并不在乎我们输出通道的大小,因为无论输入多少通道,它都能处理,分类器是最在乎。他需要知道元素个数是多少。在图中是320。其实我们可以在分类器处理之前,先将得到的张量的形状输出,得到元素个数,便于设置分类器的参数。
具体的代码实现:

我们在得到20*4*4的张量的时候要进行一次reshape,或者是view。将其转化为一个320个元素的向量。
模型代码如下:
batch_size=x.size(0):获得每一批次的数量。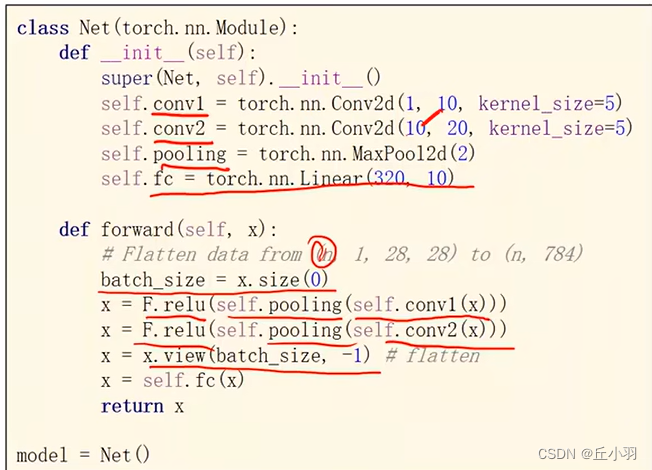
![]()
当我们有GPU的时候,我们可以使用GPU。这段话,有显卡的话,可以使用GPU。
然后我们使用model.to(device)。表示我们将这个模型放在cuda(显卡)里面计算。将CPU的功能全部迁移到GPU上面。
同时Input和target也要放在显卡上面。使用显卡来加速我们的运算过程。

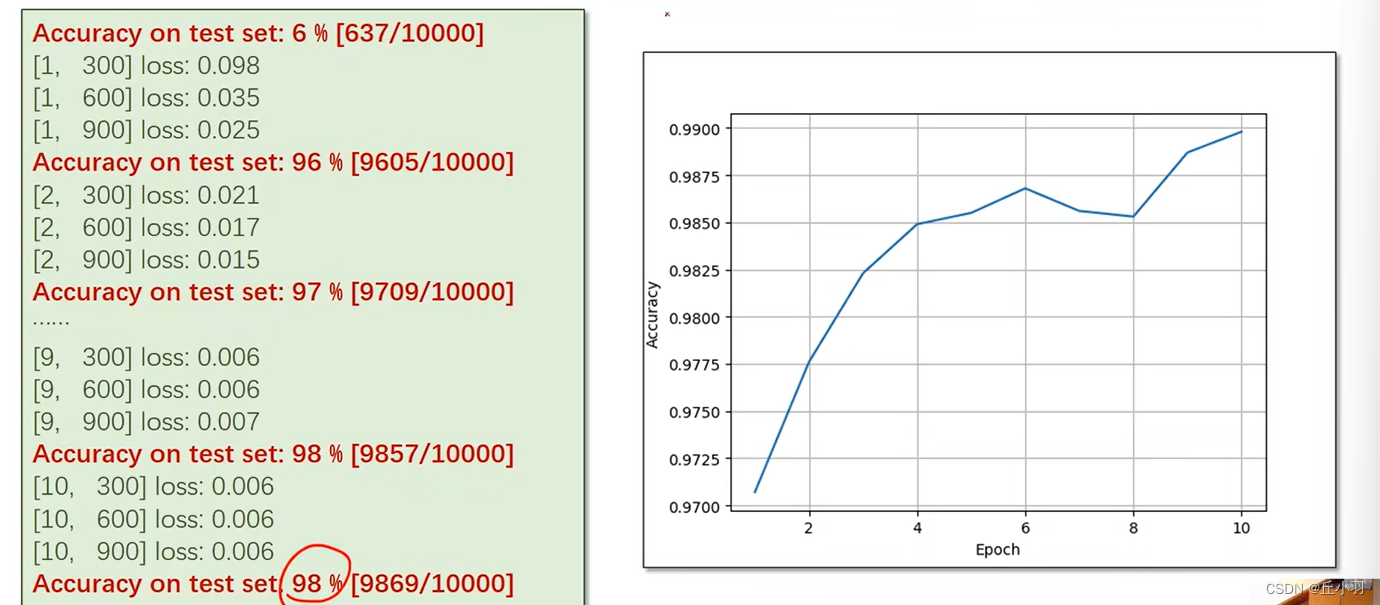
显然,训练很多轮的话,准确率提升到98%。
那么,为什么我们需要花费那么多时间从97%训练到98%呢?只增加这么一点。
我们应该从错误率的角度去考虑,我们是从3%的错误率降低到2%,提高了1/3。那这样是不是伟大很多了呢?!