在讲算法之前,我们先来思考一个问题:小明有n个编号为1~n的篮子,每个篮子里装有ai个苹果,求从 x至y 的篮子里的苹果数量之和。
如果没学过前缀和的同学,可能会打出这样的代码:

这种算法要得出一个区间之和,这题只需要取一次区间值,时间复杂度需要O(n),但如果2次,4次,1000次,数据再一大,暴力算法肯定会TLE(超时),这时前缀和的优势就体现出来了,因为它取区间之和,只需要O(1)。
那前缀和的思想是什么呢?又是如何实现用O(1)取区间之和的呢?其思想就是遍历1至n,算出1至当前数字的区间之和,有人或许会问了,那这样也无法算出特定区间之和啊,但我们观察后发现,在累加数组,前缀为右顶点的数字包含了前缀为左顶点的数字,通过用累加数组中的右顶点减去总顶点,再加上初始数组前缀为左顶点的值,可以得到:求x至y区间之和为:s[y]-s[x-1](s为累加数组)

前缀和的基本代码:

知识与要点:
前缀和不一定是和,也可以是前缀积··· ···
前缀和是一种预处理算法,能大大降低时间复杂度。
前缀和的操作对象主要是数组。
前缀和主要是计算之前数组元素的值之和。在解决区域问题时,可以减少遍历操作,减少时间复杂度。
一维前缀和:
记原数组为a[n],前缀和数组为b[n]。那么b[i]存储的内容为a[1]~a[i]的和。
即b[1]=a[1],b[2]=a[1]+a[2],b[3]=a[1]+a[2]+a[3],… 或是b[1]=b[0]+a[1],b[2]=b[1]+a[2],…(数组下标从1开始)。
公式:b[i]=a[1]+a[2]+…+a[i] (或b[i]=b[i-1]+a[i])

原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和: S[i] = a[1] +a[2] + a[3] + … + a[i]
前缀和能够快速的求出某一区间的和。
一、一维前缀和
1.前缀和是什么?
用一个简单的列子去介绍
原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和: s[i] = a[1] + a[2] + a[3] + … + a[i]
前缀和就是用一个数组s去存数组a的前n项的和。
s[0] = 0
s[1] = a[1]
s[2] = a[1] + a[2]
s[n] = a[i] + a[2] + a[3] + …+a[n]
这样s[n]对应的就是a[1]—a[n]的和,s的每一项都这样对应,就构成了前缀和。
注:前缀和的下标一定要从1开始。
2.暴力做法
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,m;
cin>>n>>m;
int sum=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
while(m--)
{
int l,r;
cin>>l>>r;
sum=0;
for(int i=l;i<=r;i++)
{
sum+=a[i];
}
cout<<sum<<endl;
}
return 0;
}这个就是用暴力的方法去做,也能求出区间[L,R]的和,但他的时间复杂度为O(n)那么当数据过于庞大的时候就会造成超时的情况。
暴力会超时。
3.前缀和求区间大小
如何利用前缀和去求区间大小呢?
有一个公式:s[r] - s[l - 1]。
就是这个公式,他的时间复杂度O(1),这就要比暴力的做法快上很多了。
3.1如何构成前缀和的形式?
for(int i=1;i<=n;i++)
s[i]=s[i-1]+a[i];s[1] = s[0] + a[1];
s[2] = s[1] + a[2];
s[3] = s[2] + a[3];
s[n] = s[n - 1] + a[n]
去遍历a数组,把当前a[n]的数加上s[n-1]的数,就能得到s[n],这个s[n]就是a[1,n]的和。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++)
s[i]=s[i-1]+a[i];
while(m--){
int l,r;
cin>>l>>r;
cout<<s[r]-s[l-1]<<endl;
}
return 0;
}二、二维前缀和
1.基本思路
二维前缀和是建立在一维前缀和的基础上实现的,唯一不同的就是,这个是二维的。
s[1][1] = s[0][1] + s[1][0] - s[0][0] + a[1][1];
s[2][2] = s[1][2] + s[2][1] - s[1][1] + a[2][2];
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
注:下标从1开始
这样理解可能有点困难,画个图就知道了。
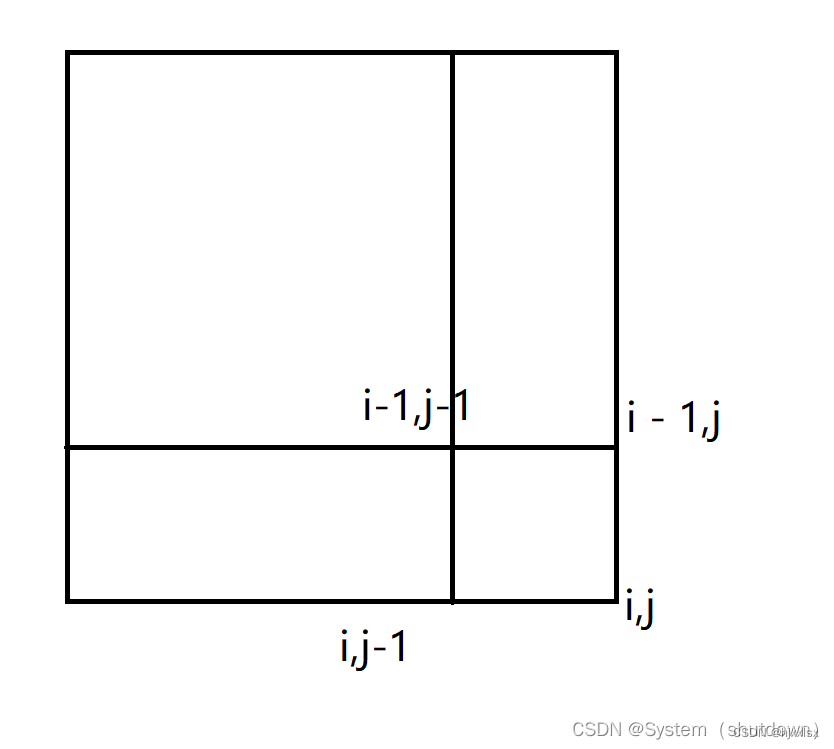
标红的区域代表的就是区间[i-1,j-1]的的和
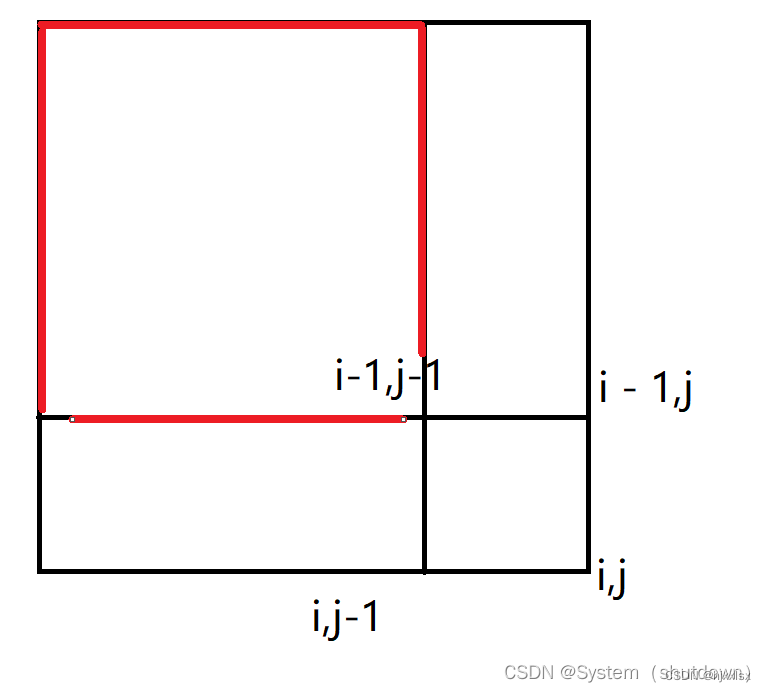
标绿的区域就是区间[i-1,j]的和
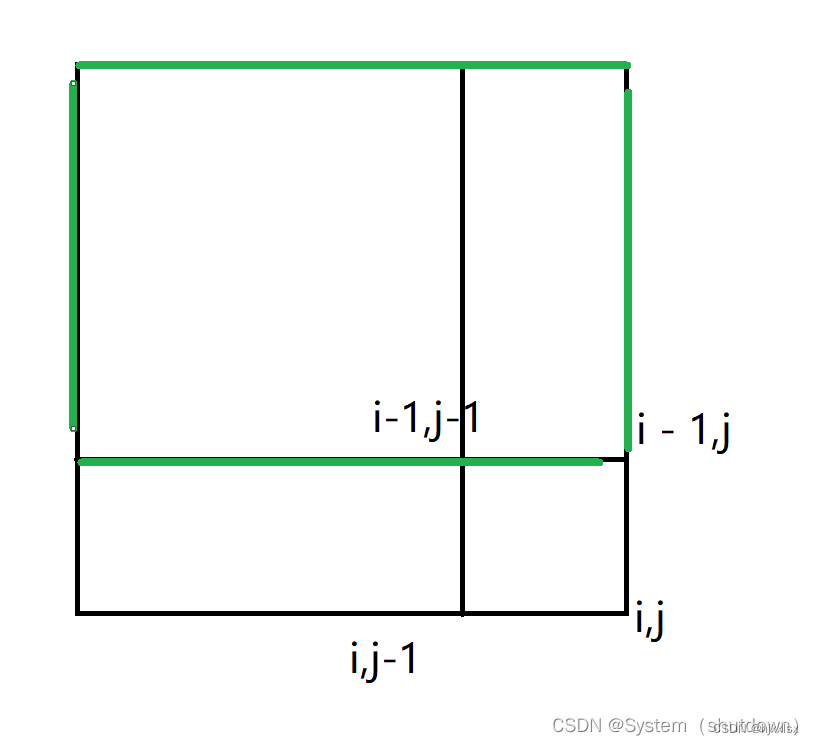
标蓝的区域就是区间[i,j-1]的和
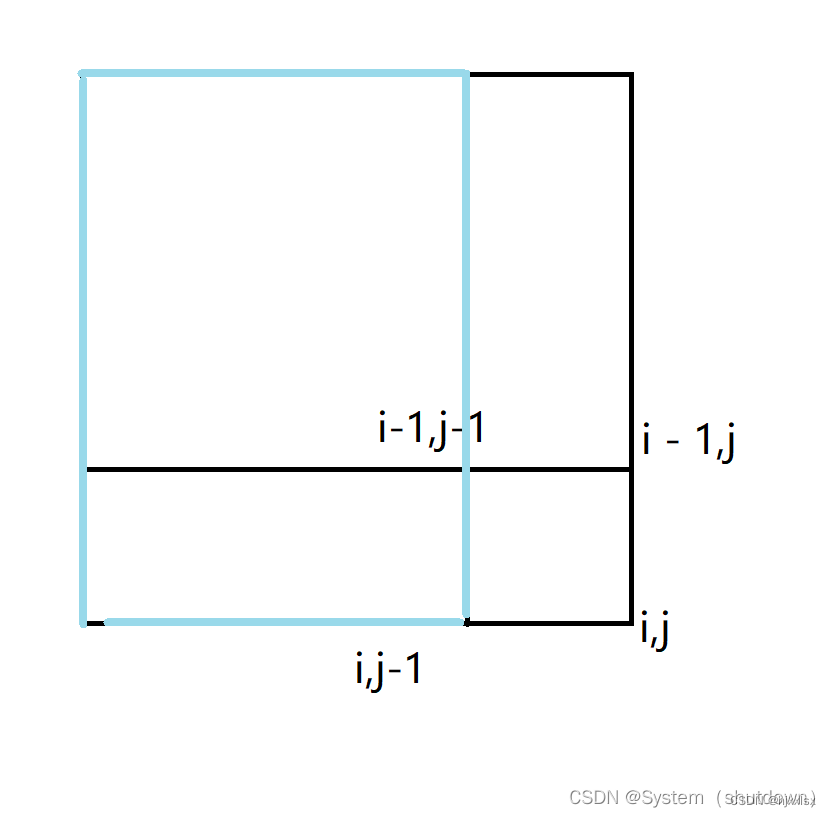
这个整体代表的就是区间[i,j]的和

由此可以看出,在计算s[i,j]的和的时候,是不是把区间s[i-1,j-1]多算了一次,所以应该把s[i-1,j-1]减去一次,就能得到区间s[i,j]正确的区间和了。
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int a[N][N],s[N][N];
int main(){
int n,m,q;
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
while(q--){
int x1,x2,y1,y2;
cin>>x1>>y1>>x2>>y2;
cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl;
}
return 0;
}1. 前缀和的定义
对于一个给定的数列A,他的前缀和数中 S 中 S[ i ] 表示从第一个元素到第 i 个元素的总和。
如下图:绿色区域的和就是前缀和数组中的 S [ 6 ]。

这里你可能就会有一个疑问?为什么是 S[ 6 ] 的位置,而不是 S[ 5 ] 的位置呢??即前缀和组中 S[ 0 ] 并没有参与求和的运算。这里先卖个关子等会在做解释。
2. 一维前缀和
2.1 计算公式
前缀和数组的每一项是可以通过原序列以递推的方式推出来的,递推公式就是:S[ i ] = S[ i - 1 ] + A[ i ]。S[ i - 1 ] 表示前 i - 1 个元素的和,在这基础上加上 A[ i ],就得到了前 i 个元素的和 S [ i ]。
2.2 用途
一维前缀和的主要用途:求一个序列中某一段区间中所有元素的和。有如下例子:
有一个长度为 n 的整数序列。
接下来输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中第 l 个数到第 r 个数的和。
这边是对前缀和的应用,如果用常规的方法:从 l 到 r 遍历一遍,则需要O(N)的时间复杂度。但是有前缀和数组的话,我们可以直接利用公式:sum = S[ r ] - S[ l - 1 ],其中sum是区间中元素的总和,l 和 r 就是区间的边界。下图可帮助理解这个公式。
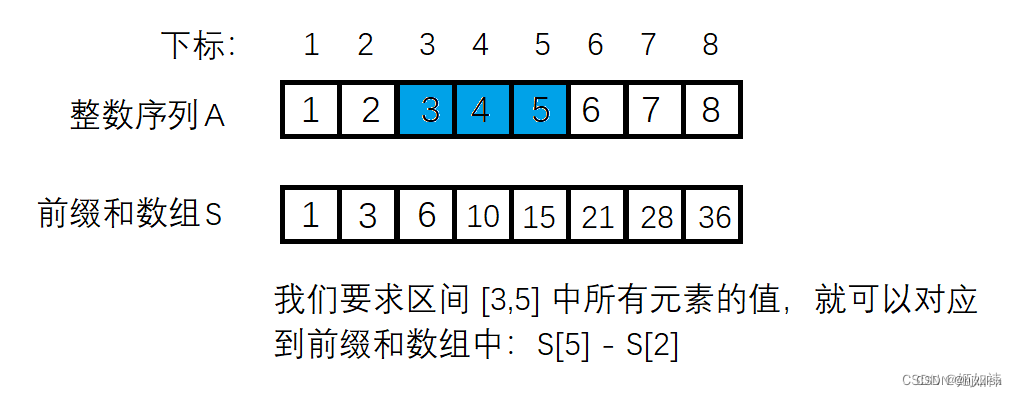
当我们要求的是序列 A 的前 n 个数之和时,如果我们是从下标为 0 的位置开始存储前缀和数组,此公式:sum = S[ r ] - S[ l - 1 ] 显然就无法使用了,为了是这个公式适用于所有情况,我们将从下标为 1 的位置开始存储前缀和,并且将下标为 0 的位置初始化为 0。
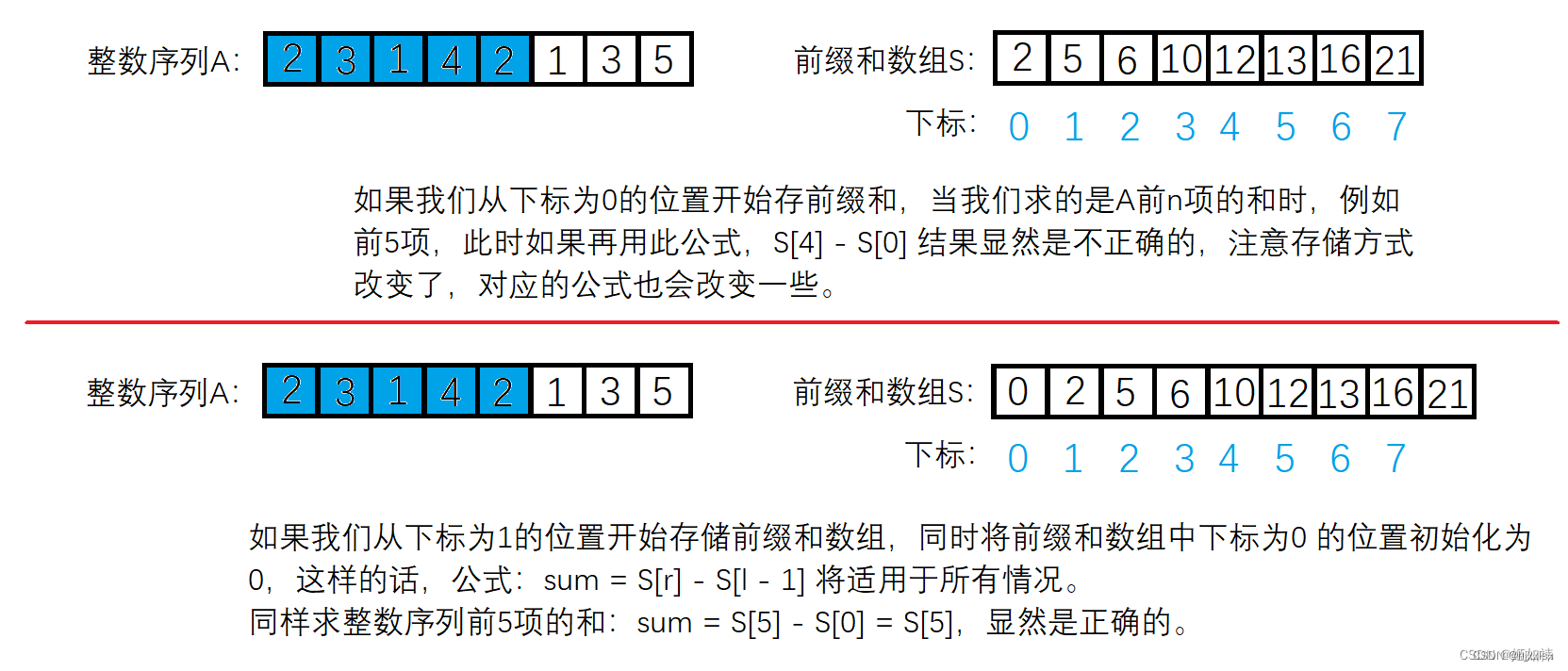
这便是为什么 S[ 0 ] 并未参与求和的运算。
有了上面的分析我们就能轻松解决这道题啦!
有一个长度为 n 的整数序列。
接下来输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数,表示整数数列。
接下来m行,每行包含两个整数l和r,表示一个询问区间的范围。
void test01(){
const int N = 100;
int a[N] = { 0 };
int s[N] = { 0 };
int n, m;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
s[i] = s[i - 1] + a[i];
}
while (m--)
{
int l, r;
scanf("%d %d", &l, &r);
printf("%d\n", s[r] - s[l - 1]);
}
}
int main()
{
test01();
system("pause");
return 0;
}3. 二维前缀和
和一维前缀和的原理类似,只不过二维前缀和求的是一个矩阵中所有元素的和。

例如:对与 x = 4,y = 3 这么一组输入,就是将原矩阵序列中蓝色区域的元素相加,得到的结果便是前缀和矩阵S中 S[ 4 ][ 3 ] 的值。
3.1 用途
一维前缀和求的是某一个区间中所有元素的和,那么二维前缀和就是求一个大矩阵中某个小的矩阵中所有元素的和。

例如上图:我们要求蓝色矩阵中所有元素的和。

现在就差最后一步了,怎么求出前缀和矩阵中的每一个值嘞??同理利用递推关系求就阔以啦。
S[ i ][ j ] = S[ i - 1 ][ j ] + S[ i ][ j - 1 ] - S[ i - 1][ j - 1 ] + a[ i ][ j ]
其中a为原矩阵序列。可以尝试举一个具体的例子来理解。
有了以上知识,我们可以尝试写代码求一下。
输入一个n行m列的矩阵,在输入q个询问,每个询问包含四个整数x1,y1,x2,y2,表示一个子矩阵左上角的坐标和右下角的坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数n,m,q
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含四个整数x1,y1,x2,y2,表示一组询问。
void test02()
{
//定义数组的大小
const int N = 100;
//原矩阵序列a
int a[N][N] = { 0 };
//前缀和矩阵,同样需要初始化为0,原因同一维矩阵
int s[N][N] = { 0 };
//读入一个n * m 的矩阵
int n, m, q;
scanf("%d %d %d", &n, &m, &q);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
scanf("%d", &a[i][j]);
//读入矩阵的同时求前缀和
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
}
//q个询问
while (q--)
{
int x1, y1, x2, y2;
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
//利用前面推导过的公式直接打印数据即可
printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
}
printf("\n");
}
int main()
{
//二维前缀和
test02();
system("pause");
return 0;
}前缀和正如字面意思,用一个新数组把旧数组每个位置的前缀和存起来,希望下面的内容能加深大家对前缀和的理解。
二、前缀和
1、基本概念
数组 a[0]~a[n-1],前缀和 sum[i] 等于 a[0]~a[i] 的和:sum[0]=a[0]、sum[1]=a[0] +a[1]、sum[2] = a[0] + a[1] + a[2].......
能在 O(n) 时间内求得所有前缀和:sum[i] = sum[i-1] + a[i]
预计算出前缀和,能快速计算出区间和:a[i] + a[i+1] + ... + a[ j-1 ] + a[ j ] = sum[ j ] - sum[i-1]
复杂度为 O(n) 的区间和计算,优化到了 O(1) 的前缀和计算
2、前缀和与差分的关系
一维差分数组 D[k] = a[k] - a[k-1],即原数组 a[ ] 的相邻元素的差。

差分是前缀和的逆运算:把求 a[k] 转化为求 D 的前缀和
3、差分数组能提升修改的效率
把区间 [L,R] 内每个元素 a[ ] 加上 d,只需要把对应的 D[ ] 做以下操作:
(1)把 D[L] 加上 d:D[L] += d
(2)把 D[R+1] 减去 d:D[R+1] -= d
原来需要 O(n) 次计算,现在只需要 O(1)
前缀和 a[x] = D[1] + D[2] + ... + D[x],有:
(1)1≤x<L,前缀和 a[x] 不变;
(2) L≤x≤R,前缀和 a[x] 增加了 d;
(3) R<x≤N,前缀和 a[x] 不变,因为被 D[R+1] 中减去的 d 抵消了。
三、例题
1、统计子矩阵(lanqiao2109,2022年省赛)
【题目描述】
有 K 位小朋友到小明家做客。小明拿出了巧克力招待小朋友们。小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足:(1)形状是正方形,边长是整数;(2)大小相同。
例如一块 6×5 的巧克力可以切出 6 块 2×2 的巧克力或者 2 块 3×3 的巧克力。小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少?
【输入描述】
第一行包含两个整数 N,K (1<=N, K<=10^5)。以下 N 行每行包含两个整数 Hi,Wi (1<=Hi,Wi<=10^5)。输入保证每位小朋友至少能获得一块1×1 的巧克力。
【输出描述】
输出切出的正方形巧克力最大可能的边长。
【问题描述】
给定一个 N×M 的矩阵A,请你统计有多少个子矩阵 (最小 1×1,最大 N×M),满足子矩阵中所有数的和不超过给定的整数K ?
【输入格式】
第一行包含三个整数 N, M和K,之后 N 行每行包含 M 个整数,代表矩阵 A。
【输出格式】
一个整数代表答案。
【样例输入】
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
【样例输出】
19
【评测用例规模与约定】
30%的数据,N, M<=20 5分
70%的数据,N, M<=100 10分
100%的数据,1<=N, M<=500 15分
0<=Aij<=1000;1<=K<=250000000
下面一起看看上面三种分数对应的解法!
(1)处理输入
【输入格式】
第一行包含三个整数 N,M 和 K,之后 N 行每行包含 M 个整数,代表矩阵 A。
Python如何读矩阵?定义矩阵 a[][] 从 a[1][1] 读到 a[n][m]
按照下面这样读入可以节省内存,每行的列表开始的时候只有一个元素。
(2)方法一:纯暴力(30%)
【思路】
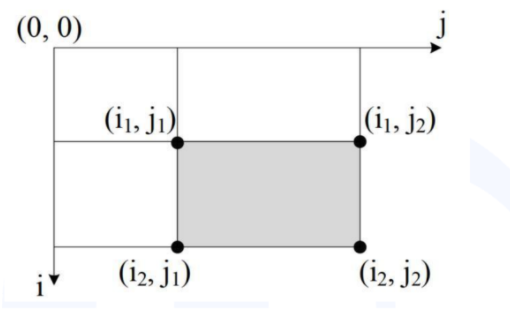
用 i1、i2、j1、j2 框出一个子矩阵
用 i、j 两重 for 循环统计子矩阵和
【复杂度】
6 个 for 循环,O(N^6)
n,m,k=map(int,input().split())
a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))
for i in range(1,n+1): #从a[1][1]开始,读矩阵
a[i].extend(map(int,input().split()))
ans=0
for i1 in range(1,n+1):
for i2 in range(i1,n+1):
for j1 in range(1,m+1):
for j2 in range(j1,m+1):
summ=0
for i in range(i1,i2+1):
for j in range(j1,j2+1):
summ+=a[i][j]
if summ<=k:
ans+=1
print(ans)(3)方法二:前缀和(70%)
【思路】
“二维前缀和”,定义 s[ ][ ]:s[ i ][ j ] 表示子矩阵 [1, 1]~[i, j] 的和
(1)预计算出 s[ ][ ],然后快速计算二维子区间和;
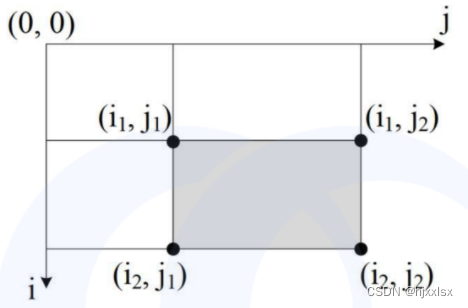
(2)阴影子矩阵 [i1, j1] ~ [i2, j2] 区间和,等于:s [i2][j2] - s[i2][j1-1] - s[i1-1][j2] + s[i1-1][j1-1]
其中 s[i1-1][ j1-1] 被减了 2 次,需要加回来 1 次。
【复杂度】
4个for循环,O(N^4)
【预计算前缀和】
“二维前缀和”,定义 s[ ][ ]: s[i][j] 表示子矩阵 [1, 1]~[i, j] 的和
n,m,k=map(int,input().split())
a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))
for i in range(1,n+1): #从a[1][1]开始,读矩阵
a[i].extend(map(int,input().split()))
s=[[0]*(m+1) for i in range(n+1)] #预计算前缀和s[][]
for i in range(1,n+1):
for j in range(1,m+1):
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]【计算子矩阵和】
阴影子矩阵 [i1, j1] ~ [i2, j2] 区间和,等于:
s[i2][j2] - s[i2][j1-1] - s[i1-1][j2] + s[i1-1][i1-1]
n,m,k=map(int,input().split())
a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))
for i in range(1,n+1): #从a[1][1]开始,读矩阵
a[i].extend(map(int,input().split()))
s=[[0]*(m+1) for i in range(n+1)] #预计算前缀和s[][]
for i in range(1,n+1):
for j in range(1,m+1):
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]
ans=0
for i1 in range(1,n+1):
for i2 in range(i1,n+1):
for j1 in range(1,m+1):
for j2 in range(j1,m+1):
sum=s[i2][j2]-s[i2][j1-1]-s[i1-1][j2]+s[i1-1][j1-1]
if sum<=k:
ans+=1
print(ans)(4)方法三:前缀和+尺取法(100%)
【思路】
本题统计二维子矩阵和 <=k 的数量,而不用具体指出是哪些子矩阵,可以用尺取法优化。
以一维区间和为例,查询有多少子区间 [j1, j2] 的区间和 s[j2] - s[j1] ≤ k。

暴力法
用 2 重 for 循环遍历 j1 和 j2,复杂度O(n^2)。
尺取法求一维区间和
若 s[j2] - s[j1] <= k,那么在子区间 [j1, j2] 上,有 j2 - j1 + 1 个子区间满足 <= k。用同向扫描的尺取法,用滑动窗口 [j1, j2] 遍历,复杂度降为 O(n)。
尺取法求二维区间和
矩阵的行子区间和仍用 2 重暴力遍历
只把列区间和用尺取法优化
n,m,k=map(int,input().split())
a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))
for i in range(1,n+1): #从a[1][1]开始,读矩阵
a[i].extend(map(int,input().split()))
s=[[0]*(m+1) for i in range(n+1)] #预计算前缀和s[][]
for i in range(1,n+1):
for j in range(1,m+1):
s[i][j]=s[i-1][j]+a[i][j] #第9行
ans=0
for i1 in range(1,n+1):
for i2 in range(i1,n+1):
j1=1;z=0
for j2 in range(1,m+1):
z+=s[i2][j2]-s[i1-1][j2] #第15行
while z>k:
z-=s[i2][j1]-s[i1-1][j1]
j1+=1
ans+=j2-j1+1
print(ans)第9行,求第 j 列上,第 1 行到第 i 行上数字的前缀和。
第 11、12 行用 2 重暴力遍历行。
第 14 行:尺取法,滑动窗口 [j1, j2]。移动指针 j2

第15行:第 j2 列上,i1~i2 的区间和。累加得到二维区间和
第16行:若区间和 >k,移动指针 j1
第19行:若 j1~j2 的区间和 <k,那么有 j2-j1+1 个满足
【复杂度】
3 个 for 循环,O(N^3) 刚刚能通过题目的 100% 测试。
(5)个人拙见
Python 组可能不会出这种题,这一题是 C/C++ B组题
Python 的 for 循环极慢,1千万次的循环超过10秒。本题100%的测试运行时间超过10秒。
2、灵能传输(lanqiaoOJ题号196)
题目描述
题目背景
在游戏《星际争霸 II》中,高阶圣堂武士作为星灵的重要 AOE 单位,在 游戏的中后期发挥着重要的作用,其技能"灵能风暴"可以消耗大量的灵能对一片区域内的敌军造成毁灭性的伤害。经常用于对抗人类的生化部队和虫族的刺蛇飞龙等低血量单位。
问题描述
你控制着 n 名高阶圣堂武士,方便起见标为 1,2,⋅⋅⋅,n。每名高阶圣堂武士需要一定的灵能来战斗,每个人有一个灵能值 ai 表示其拥有的灵能的多少,ai 非负表示这名高阶圣堂武士比在最佳状态下多余了 ai 点灵能,ai 为负则表示这名高阶圣堂武士还需要 −ai 点灵能才能到达最佳战斗状态)。

输入描述

输出描述
输出 T 行。每行一个整数依次表示每组询问的答案。
输入输出样例
输入:
3
3
5 -2 3
4
0 0 0 0
3
1 2 3
输出:
3
0
3
运行限制
最大运行时间:1s
最大运行内存: 256M
这题和前缀和有关:
(1)所有加减操作都是在数组内部进行,也就是说对于整个数组的和不会有影响;
(2)一次操作是对连续的 3 个数 a[i-1]、a[i]、a[i+1],根据 a[i-1]+=a[i],a[i+1]+=a[i], a[i]=-2a[i],得前缀和 s[i+1] 的值不变,因为这些数的加减都是在 a[i-1]、a[i]、a[i+1] 内部进行的。另外三个数的和不变。
分析一次操作后的前缀和:
(1)a[i-1] 更新为 a[i]+a[i-1],那么 s[i-1] 的新值等于原来的 s[i];
(2)a[i] 更新为 -2a[i],那么 s[i] 的新值等于原来的 s[i-1];
(3)a[i+1] 更新为 a[i]+a[i+1],s[i+1]的值保持不变。
经过一次操作后,s[i] 和 s[i-1] 互相交换,s[i+1] 不变。而 s[i-1]、s[i]、 s[i+1] 这 3 个数值还在,没有出现新的数值。设 a[0]=0,观察前缀和数组 s[0]、 s[1]、 s[2]、 ...、s[n-1]、s[n]。除了 s[0]、s[n] 外,其他的 s[1]、s[2]、…、s[n-1],经过多次操作后,每个 s[i] 能到达任意位置。
也就是说,题目中对 a[ ] 的多次操作后的一个结果,对应了前缀和 s[ ] 的一种排列。因为 a[i]=s[i]-s[i1],对 a[ ] 多次操作后的结果是:
a[1] = s[1] - s[0],a[2] = s[2] - s[1],...,a[n] = s[n] - s[n-1]
经过以上转换,题目的原意 “对连续 3 个数做加减操作后,求最大的 a[ ] 能达到多小”,变成了比较简单的问题 “数组 s[],求 max{|s[1]-s[0]|,|s[2]-s[1]|, ..., |s[n]-s[n-1]|}”。
根据题目的要求,s[0] 和 s[n] 保持不动,其他 s[ ] 可以随意变换位置。
先看一个特殊情况,若 s[0] 是最小的, s[n] 是最大的,那么简单了,把 s[ ] 排序后, max{ |s[i]-s[i-1]| ]就是解。

若 s[0] 不是最小的,s[n] 不是最大的,事情比较麻烦。先把 s[ ] 排序,s[0] 和 s[n] 在中间某两个位置,见下图。

此时应该从 s[0] 出发,到最小值 min,然后到最大值 max,最后到达 s[n],如图所示路线 1->2->3,这样产生的 |s[i]-s[i-1]| 会比较小。
最后一个问题是,图中存在重叠区,[min, s0] 和 [sn, max] 上有重叠。例如在 [min, s0] 上来回走了两遍,但是这区间的每个数只能用一次,解决办法是隔一个数取一个。
还有一个问题,如何处理重叠区?用 vis[i]=1 记录第一次走过的时候第 i 数被取过,第二次再走过时,vis[ ]=1 的数就不用再取了。
本题难在思维,代码好写。
T=int(input())
for t in range(T):
n=int(input())
a=list(map(int,input().split()))
s=[0]+a
for i in range(1, n+1):
s[i] += s[i-1] #前缀和
s0=0
sn=s[n]
if s0>sn:
sn,s0=s0,sn #交换:swap(s0, sn)
s. sort()
for i in range(n+1): #找s[0]和s[n]的位置
if s[i]==s0:
s0 = i
break
for i in range(n,-1,-1):
if s[i]==sn:
sn = i;
break
L,R=0,n
a=[0 for i in range(n+1)]
a[n]=s[n]
vis=[True for i in range(n+1)]
for i in range(s0,-1,-2):
a[L]=s[i];
L+=1;
vis[i]=False
for i in range(sn, n+1,2):
a[R]=s[i];
R-=1;
vis[i]=False
for i in range(n+1):
if vis[i]:
a[L]=s[i]
L+=1
res = 0
for i in range(n):
res=max(res,abs(a[i+1]-a[i]))
print (res)前缀和概念
前缀和:顾名思义,是要求前缀的总和,什么是前缀,对于一个存放数字的数组而言,前缀就是指的数组的前k项,因此对应的前缀和就是数组前k项的和。前缀和一般用来求数组中连续段子数组的值的和,类似于等差数列中利用等差数列的和来求某一段子数列的和:![]()
public int[] prefix(int[] arr){
int[] prefixArr = new int[arr.length];
//前缀和的第一项与数组的第一项相同
prefixArr[0] = arr[0];
for(int i = 1; i < arr.length;i++){
//从第二项开始,之后每一项都等于前一项加上对应数组项
prefixArr[i] = prefixArr[i-1] + arr[i];
}
return prefixArr;
}
前缀和例题
题目介绍
思路分析
当我们刚看到这道题时,直接想到的方法就是将这个数组的乘积求出来,然后遍历该数组,新数组的每一项都等于原数组的乘积除以该项的值即可。但奈何力扣不作美,偏偏在题目下方给你"摁下回车键":不能使用除法。因此,我们不用这种人人都能想到的方法,当然,这种方法也可以使用,但在使用的时候要注意当某一项的元素为0时,用除法进行运算会出现错误,因此要特别考虑。
我们利用前缀和的思想来解决这道题:从题目的说明中我们可以看到,我们需要在遍历一次数组的情况下来求解出新数组的每一项元素,当然对于准备工作中的遍历不再考虑范围之内。
通过分析可以看到,新数组当中的每一项元素都等于原数组中对应位置的前面所有元素的乘积与后面元素所有乘积的乘积。因此我们可以先求出前缀积和后缀积。通过观察我们可以发现新数组的每一项都等于原数组对应位置的前一项的前缀积和后一项的后缀积的乘积,对于首尾元素而言,他们分别没有前一项和后一项,如图所示:

相关代码
public int[] productExceptSelf(int[] nums) {
int len = nums.length;
//新的数组
int[] output = new int[len];
//前缀积数组
int[] cn = new int[len];
//后缀积数组
int[] bn = new int[len];
cn[0] = nums[0];
bn[0] = nums[len - 1];
for (int i = 1; i < len - 1; i++) {
//求前缀积和后缀积数组
cn[i] = nums[i] * cn[i - 1];
bn[i] = nums[len - 1 - i] * bn[i - 1];
}
//新数组的第一项和最后一项单独考虑
output[0] = bn[len - 2];
output[len - 1] = cn[len - 2];
for (int i = 1; i < len - 1; i++) {
//新数组的中间的每一项的计算
output[i] = cn[i - 1] * bn[len - 2 - i];
}
return output;
1.前缀和的数组型简单定义
对于数组nums来说,前缀和pre[i] = pre[i-1] + nums[i],即每个位置上存储的是前i个数组元素的和,用数学公式表示为:
数组的典型案例:
其他类型的前缀和多是最终能变成和数量相关,即转换成int[] 数组类型。
那么,对于后缀和是一样的道理。
2.前缀和的典型使用场景/触发关键词
在一些题目或者场景中,出现了子数组*,连续一段区间,并且和求数量或者判断数量相关,很大程度上可以向前缀和的方去思考。
二. 使用前缀和的经典案例

1.leetcode1413 逐步求和得到正数的最小值
给你一个整数数组 nums 。你可以选定任意的 正数 startValue 作为初始值。
你需要从左到右遍历 nums 数组,并将 startValue 依次累加上 nums 数组中的值。
请你在确保累加和始终大于等于 1 的前提下,选出一个最小的 正数 作为 startValue 。
输入:nums = [-3,2,-3,4,2]
输出:5
解释:如果你选择 startValue = 4,在第三次累加时,和小于 1 。
累加求和
startValue = 4 | startValue = 5 | nums
(4 -3 ) = 1 | (5 -3 ) = 2 | -3
(1 +2 ) = 3 | (2 +2 ) = 4 | 2
(3 -3 ) = 0 | (4 -3 ) = 1 | -3
(0 +4 ) = 4 | (1 +4 ) = 5 | 4
(4 +2 ) = 6 | (5 +2 ) = 7 | 2对于本题,可以转化为求一类最小值问题,即前缀和中出现的最小值,即在遍历整个数组时,可能出现的最小值,即

只要最小值能够满足要求,那么在其他位置上也可以满足要求,上述出现的sum(1)~sum(n)即为典型的前缀和的概念,换个思路,此题目在求能使得数组通过的最小宽度,即

前缀和解答
class Solution {
public int minStartValue(int[] nums) {
int[] dp = new int[nums.length];
int min = nums[0];
dp[0] = nums[0];
for(int i = 1; i < nums.length; i++){
dp[i] += dp[i-1]+nums[i];
if(dp[i] < min){
min = dp[i];
}
}
if(min > 0) return 1;
return 1-min;
}
}动态规划空间优化
对于上述解答来说,由于当前值只和nums[i]和上一个值有关,用两个变量保存交替前进即可
class Solution {
public int minStartValue(int[] nums) {
int min = 0;
int pre = 0;
for(int i = 0; i < nums.length; i++){
pre += nums[i];
if(pre <= min){
min = pre;
}
}
if(min > 0) return 1;
return 1-min;
}
}本题小结:(1)此题是前缀和的最简单应用,最终的答案和前缀和的最大值相关
2.leetcode2383 赢得比赛需要的最少训练时长
你正在参加一场比赛,给你两个 正 整数 initialEnergy 和 initialExperience 分别表示你的初始精力和初始经验。
另给你两个下标从 0 开始的整数数组 energy 和 experience,长度均为 n 。
你将会 依次 对上 n 个对手。第 i 个对手的精力和经验分别用 energy[i] 和 experience[i] 表示。当你对上对手时,需要在经验和精力上都 严格 超过对手才能击败他们,然后在可能的情况下继续对上下一个对手。
击败第 i 个对手会使你的经验 增加 experience[i],但会将你的精力 减少 energy[i] 。
在开始比赛前,你可以训练几个小时。每训练一个小时,你可以选择将增加经验增加 1 或者 将精力增加 1 。
返回击败全部 n 个对手需要训练的 最少 小时数目。
输入:initialEnergy = 5, initialExperience = 3, energy = [1,4,3,2], experience = [2,6,3,1]
输出:8
解释:在 6 小时训练后,你可以将精力提高到 11 ,并且再训练 2 个小时将经验提高到 5 。
按以下顺序与对手比赛:
- 你的精力与经验都超过第 0 个对手,所以获胜。
精力变为:11 - 1 = 10 ,经验变为:5 + 2 = 7 。
- 你的精力与经验都超过第 1 个对手,所以获胜。
精力变为:10 - 4 = 6 ,经验变为:7 + 6 = 13 。
- 你的精力与经验都超过第 2 个对手,所以获胜。
精力变为:6 - 3 = 3 ,经验变为:13 + 3 = 16 。
- 你的精力与经验都超过第 3 个对手,所以获胜。
精力变为:3 - 2 = 1 ,经验变为:16 + 1 = 17 。
在比赛前进行了 8 小时训练,所以返回 8 。
可以证明不存在更小的答案。class Solution {
public int minNumberOfHours(int initialEnergy, int initialExperience, int[] energy, int[] experience) {
int preen = initialEnergy;
int preex = initialExperience;
int exermax = 0;
int len = energy.length;
for(int i = 0; i < len; i++){
preen -= energy[i];
if(preex <= experience[i]){
int diff = experience[i]-preex+1;
exermax = Math.max(exermax,diff);
}
preex += experience[i];
}
if(preen <= 0){
preen = 0-preen+1;
}
else{
preen = 0;
}
return preen + exermax;
}
}1. 对于精力来说,一直减少,那么直接一直减去就好了
1.1 最后小于0 证明初值无法覆盖所有的精力,取反+1
1.2 最后大于0 证明初值可以覆盖所有的精力,不需要额外的精力2. 对于经验来说,适当更新(特定地方更新)
2.1 当前缀和无法覆盖当前经验,进行更新,更新的值是前缀和与当前值的差值
2.2 当前缀和可以覆盖当前经验,无需额外的经验本题小结:(1)本题目只需要在经验部分使用前缀和,精力其实是符合贪心原则,即一直减去就好了,一直是最优值(最后需要的答案值)
(2)前缀和不需要留存,与数组当前值比较即可
三. 前缀和的好搭档:动态规划和HashMap
在实际的题目中,单独使用前缀和可以解决问题,但有些题目受限于时间和空间复杂度,单独依靠前缀和往往不能AC,需要一些额外的技巧或者附加数据结构,例如动态规划和HashMap。
3.1 动态规划经常和前缀和一起使用
(1)leetcode1871 跳跃游戏 VII
给你一个下标从 0 开始的二进制字符串 s 和两个整数 minJump 和 maxJump 。一开始,你在下标 0 处,且该位置的值一定为 '0' 。当同时满足如下条件时,你可以从下标 i 移动到下标 j 处:
i + minJump <= j <= min(i + maxJump, s.length - 1) 且
s[j] == '0'.
如果你可以到达 s 的下标 s.length - 1 处,请你返回 true ,否则返回 false 。
输入:s = "011010", minJump = 2, maxJump = 3
输出:true
解释:
第一步,从下标 0 移动到下标 3 。
第二步,从下标 3 移动到下标 5 。动态规划
class Solution {
public boolean canReach(String s, int minJump, int maxJump) {
int n = s.length();
boolean[] dp = new boolean[n];
dp[0] = true;
for (int i = minJump; i < n; i++){
if (s.charAt(i) == '1')
continue;
int left = i - maxJump < 0 ? 0 : i - maxJump;
int right = i - minJump;
for (int j = left; j <= right; j++){
if (dp[j]){
dp[i] = true;
break;
}
}
}
return dp[n - 1];
}
}在最基础的动态规划中,我们来到第i个位置,第i个位置能不能走到,取决于之前在i- maxJump~i- minJump中是否有一个位置j,这个位置j是可以走到的,那么可得知从j可以蹦到i,如果在i- maxJump~i- minJump范围内都是不可达的,那么证明第i个位置也是不可达的。

总结
动态规划的初始条件: dp[0] = True,默认第一个元素都是‘0’,都可以走到
动态规划的递推公式:f(i) = f(i-minJump) || f(i-minJump-1) || ... || f(i-maxJump)
动态规划的终止条件:来到数组最后一个位置上述动态规划的时间复杂度肯定是很高的,在java语言下,勉强可以通过。
动态规划+前缀和
轮到前缀和出场:
class Solution {
public boolean canReach(String s, int minJump, int maxJump) {
int n = s.length();
boolean[] f = new boolean[n];
int[] pre = new int[n];
f[0] = true;
for(int i = 0; i < minJump; i++){
pre[i] = 1;
}
for(int i = minJump; i < n ; i++){
int left = i-maxJump;
int right = i-minJump;
if(s.charAt(i) == '0'){
int total = pre[right] - (left <= 0 ? 0:pre[left-1]);
if(total != 0) f[i] = true;
}
if(f[i]){
pre[i] = pre[i-1] + 1;
}
else{
pre[i] = pre[i-1];
}
}
return f[n-1];
}
}本题小结:(1)在本种解法中,前缀和保存了一定区间内可达位置的数量,前缀和之差保存了目标区间可达数量
(2)当且在前缀和不为0时,i位置才可达,可达即要更新,即在上个区间的基础上加一:pre[i] = pre[i-1] + 1
3.2 HashMap,前缀和的另外一个好搭档
在有些题目中,使用HashMap们可以极大地降低时间复杂度,尤其在解中出现两层以上for循环,其中的一层很有可能通过HashMap来优化。
(1)leetcode1590 使数组和能被 P 整除
给你一个正整数数组 nums,请你移除 最短 子数组(可以为 空),使得剩余元素的 和 能被 p 整除。 不允许 将整个数组都移除。
请你返回你需要移除的最短子数组的长度,如果无法满足题目要求,返回 -1 。
子数组 定义为原数组中连续的一组元素。
输入:nums = [3,1,4,2], p = 6
输出:1
解释:nums 中元素和为 10,不能被 p 整除。我们可以移除子数组 [4] ,剩余元素的和为 6 。动态规划(已经部分优化过)
class Solution {
public int minSubarray(int[] nums, int p) {
int len = nums.length;
int[][] dp = new int[len][len];
int min = len;
int sum = 0;
int temp = 0;
for(int i : nums){
sum += i;
temp += i;
temp %= p;
}
if(temp % p == 0) return 0;
for(int i = 0; i < len ; i++){
for(int j = i; j < len ; j++){
if(j == 0 && i == 0){
dp[i][j] = nums[j];
}
else{
dp[i][j] = dp[i][j-1] + nums[j];
}
int diff = sum-dp[i][j];
if(diff == 0) continue;
if( diff % p == 0){
int dele = j-i+1;
min = Math.min(min,dele);
}
}
}
if(min == len) return -1;
return min;
}
}
空间上达不到要求
前缀和优化
class Solution {
public int minSubarray(int[] nums, int p) {
int sum = 0;
int pre = 0;//前缀和
int min = nums.length;//保存最小值
int len = min;
HashMap<Integer,Integer> map = new HashMap<>();
for(int i : nums){
sum = (sum+i)%p;
}
if(sum == 0) return 0;
map.put(0,-1);
for(int i = 0; i < len; i++){
pre = (pre+nums[i]) % p;
int target = (pre - sum + p) %p;
if(map.containsKey(target)){
int distance = i - map.get(target);
min = Math.min(min,distance);
}
map.put(pre,i);
}
return min == len ? -1 : min;
}
} 
题目小结:(1)在本题中,若只依靠前缀和, 在两层for循环中,很容易造成时间和空间超标
(2)通过HashMap存储目标值,让时间复杂度变为O(N)
(2)面试题 17.05. 字母与数字
给定一个放有字母和数字的数组,找到最长的子数组,且包含的字母和数字的个数相同。
返回该子数组,若存在多个最长子数组,返回左端点下标值最小的子数组。若不存在这样的数组,返回一个空数组。
输入: ["A","1","B","C","D","2","3","4","E","5","F","G","6","7","H","I","J","K","L","M"]
输出: ["A","1","B","C","D","2","3","4","E","5","F","G","6","7"]class Solution {
public String[] findLongestSubarray(String[] array) {
HashMap<Integer,Integer> map = new HashMap<>();
int ct_num_i = 0;
int ct_cha_i = 0;
int len = array.length;
map.put(0,-1);
int max = 0;
int index = 0;
for(int i = 0; i < len; i++){
if(array[i].charAt(0) >= '0' && array[i].charAt(0) <= '9'){
ct_num_i++;
}
else{
ct_cha_i++;
}
int diff = ct_num_i - ct_cha_i;
if(map.containsKey(diff)){
int j = map.get(diff);
if(i - j > max){
max = i-j;
index = j+1;
}
}
else{
map.put(diff,i);
}
}
String[] ans = new String[max];
for(int i = 0; i < max; i++){
ans[i] = array[index + i];
}
return ans;
}
}本体小结:(1)此题目和上题一样,也是用过HashMap来降低时间复杂度
(2)注意此题存储的是ct_num_i - ct_cha_i,因为只存储一个类型的数量,会导致无法处理未知值,详情可看下方图片中的红色虚线框,而存储差值就比较方便,因为当满足题目要求时,我们有:
ct_num_i - ct_cha_i == ct_num_ j - ct_cha_ j ,j为i之前的某个位置。
而int diff = ct_num_i - ct_cha_i 其中的diff正是差值。

总结
本文主要介绍了一维前缀和的概念以及相关应用。当然也存在高维前缀和,但大致思路都是相同的。前缀和是一种有效的减少时间复杂度的预处理方式,在对大数据进行预处理时能够显著提升预处理的效率
有N个正整数放到数组B里,它是数组A的前缀和数组,求A数组。
输入格式
第一行1个正整数:N,范围在[1,100]。
第二行N个正整数:范围在[1,10000]。
输出格式
N个正整数。
输入/输出例子1
输入:
6
2 10 20 25 30 43
输出:
2 8 10 5 5 13
样例解释
无
#include<bits/stdc++.h>
using namespace std;
int n,a[10005],b[10005];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>b[i];
a[i]=b[i]-b[i-1];
cout<<a[i]<<" ";
}
return 0;
}给你一个正整数数组 a ,请你计算所有可能的奇数长度子数组的和。
子数组 定义为:原数组中的一个连续子序列。
请你输出数组 a 中所有奇数长度子数组的和。
输入格式
第1行:1个正整数N,不超过10000。
第2行:N个整数,范围[1,1000]。
输出格式
输出一个整数。
输入/输出例子1
输入/输出例子1
输入:
5
1 4 2 5 3
输出:
58
样例解释
所有奇数长度子数组和它们的和为:
[1] = 1
[4] = 4
[2] = 2
[5] = 5
[3] = 3
[1,4,2] = 7
[4,2,5] = 11
[2,5,3] = 10
[1,4,2,5,3] = 15
我们将所有值求和得到 1 + 4 + 2 + 5 + 3 + 7 + 11 + 10 + 15 = 58
#include<bits/stdc++.h>
using namespace std;
long long n,a[10005],b[10005],s=0;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=b[i-1]+a[i];
}
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j+=2)
s+=b[j]-b[i-1];
cout<<s;
return 0;
}
小明很喜欢喜欢数字1,他想研究两个整数之间所有整数出现了多少个数字1。
现在他想求n次,a和b之间(包含a和b)的所有整数的1出现的次数,聪明的你能够帮帮小明吗?
输入格式
第一行一个整数n(1<=n<=1000000)。
下面有n行,每行 2 个整数 a 和 b(1<=a,b<=1000000)。
输出格式
n个整数,每个数一行,对应 n个询问。
输入/输出例子1
输入:
3
1 10
10 20
5 9
输出:
2
11
0
#include<bits/stdc++.h>
using namespace std;
int fen(int x){
int s=0;
while(x>0){
if(x%10==1)s++;
x/=10;
}
return s;
}
long long n,a[1000000+5],b[1000000+5];
int main(){
for(int i=1;i<=1000000;i++){
a[i]=fen(i);
b[i]=b[i-1]+a[i];
}
cin>>n;
while(n--){
int x,y;
scanf("%d%d",&x,&y);
printf("%d\n",b[y]-b[x-1]);
}
return 0;
}输入n个整数组成的序列A,序列的编号从1到n。
统计有多少个连续的一段和A[s]+A[s+1]+ A[s+2]+…+A[e]能被7整除。
输入格式
第一行,n,表示有n个整数。(n<=1000)
第二行,n个1000以内的整数。
输出格式
一行,一个整数,表示共有多少段连续数的和能被7整除。
输入/输出例子1
输入:
5
8 7 6 9 10
输出:
2
样例解释
8+7+6=21,能被7整除 ,7能被7整除 除了上述两段连续的数的和可以被7整除,找不到其它的段。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int A[n];
for(int i=0;i<n;i++){
cin>>A[i];
}
int count=0;
for(int i=0;i<n;i++){
int sum=0;
for(int j=i;j<n;j++){
sum+=A[j];
if(sum%7==0){
count++;
}
}
}
cout<<count<<endl;
return 0;
}
桐桐想统计某个区间范围里的素数,例如,A=2,B=10,则A和B之间(包括A、B)素数一共有4个,分别为:2,3,5,7。
现在桐桐给出N个区间范围,问每个区间有多少个素数。请你帮助她统计一下。
输入格式
第一行一个整数 N(1<=N<=10^5);
后有N行,每行两个整数A B(1<=A<=B<=10^5),用空格隔开,表示一个区间范围。
输出格式
共N行,每行一个整数,对应区间范围的素数个数。
输入/输出例子1
输入:
2
2 8
1 13
输出:
4
6
样例解释
无
#include<bits/stdc++.h>
using namespace std;
long long jk[1000002],n,m,q,x,y,a[10000002],b[10000002];
int main(){
cin>>q;
for(int i=2;i<=10000002;i++)
{
if(a[i]!=0)continue;
for(long long j=i*2;j<=10000002;j+=i)a[j]=1;
}
for(long long i=2;i<=10000002;i++)
{
if(a[i]==0)
for(int j=2;;j++)
{
if(i*j>10000002)break;
a[i*j]=1;
}
}
for(long long i=2;i<=10000002;i++)
{
if(a[i]==0)b[i]=b[i-1]+1;
else if(a[i]==1)b[i]=b[i-1]+0;
}
for(long long i=1;i<=q;i++)
{
scanf("%lld%lld",&x,&y);
printf("%lld\n",b[y]-b[x-1]);
}
return 0;
}