300. 任务安排1(300. 任务安排1 - AcWing题库)

思路:很明显这些任务是按顺序排好的,我们能执行的操作只是对它们进行分批,我们可以发现每一批之前的开始时间s,影响的不仅仅是当前这一批的结束时间,而是将后面所有的结束时间都往后推了s,那么我们直接把对于后面的影响全部提到当前位置来算,那么批与批之间就相对独立一点了。
我们这么来定义,定义dp[i]表示第i个物品作为当前这批的末尾,那么我们就可以通过对上一批的末尾进行讨论进而划分批次,上一批的末尾可以从1一直到i-1。
令sc作为费用的前缀和,st作为时间的前缀和
那么状态转移就是:
dp[i]=min(dp[j]+(sc[i]-sc[j])*st[i]+s*(sc[n]-sc[j]));//因为前面的s对于当前的影响已经被计算到之前批次中了,所以我们这里只用计算当前批次的影响即可。
那么显然时间复杂度是O(n^2),对于这题的数据范围来说是可以ac的。
另外因为这道题求的是最小值,所以说,我们初值要赋成正无穷。
#include<bits/stdc++.h>
using namespace std;
#define int long long
int t[6000],c[6000],dp[6000];
signed main()
{
int n,s;
scanf("%lld%lld",&n,&s);
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&t[i],&c[i]);
c[i]+=c[i-1];
t[i]+=t[i-1];
}
memset(dp,0x3f,sizeof dp);
dp[0]=0;
for(int i=1;i<=n;i++)
{
for(int j=0;j<i;j++)
{
dp[i]=min(dp[i],dp[j]+(c[i]-c[j])*t[i]+s*(c[n]-c[j]));
}
}
cout<<dp[n];
}301. 任务安排2(301. 任务安排2 - AcWing题库)

在题意上较之上题没有变化,但是n的数据范围变大了。
所以递推的式子还是如上: dp[i]=min(dp[j]+(sc[i]-sc[j])*st[i]+s*(sc[n]-sc[j]));
但显然不能再用暴力去循环了,那么换个思路。我们来观察下这个式子。很容易发现,与j有关的只有两类:dp[j],sc[j],如果我们将两者一个视为自变量,一个视为因变量,那么很显然是一个一次函数:
dp[j]=(st[i]+s)*sc[j]+dp[i]-sc[i]*st[i]-s*sc[n];
显然i确定后,st[i]+s是确定的,另外对于j来说,一个j,只有一个dp[j]和一个sc[j],那么实际上就相当于将所有的j的点画在坐标系中,然后一条斜率确定的,经过这些点的直线,求满足条件的直线的截距的最小值。
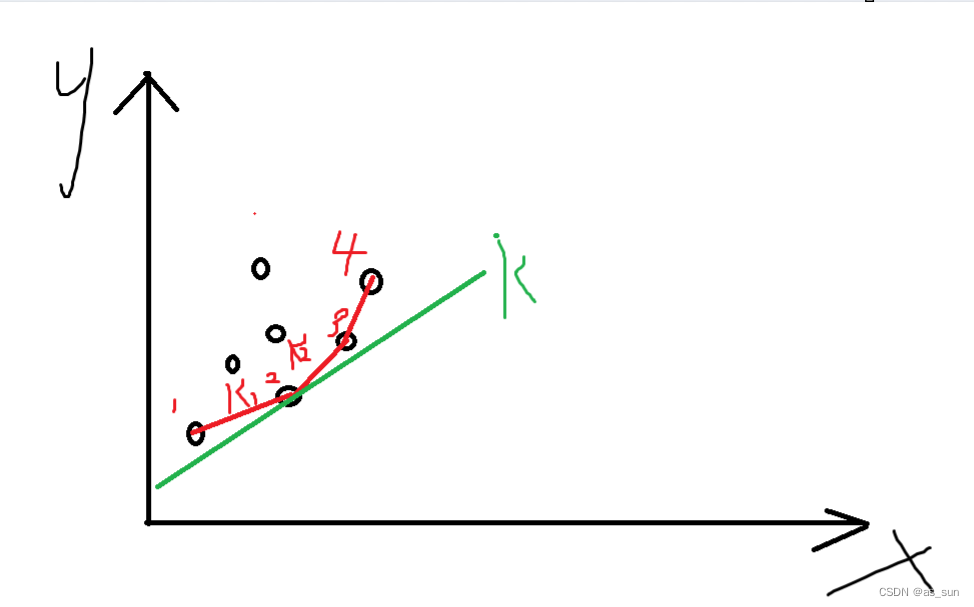
显然如果找截距最小的话,应该是图中红线上的点(相当于凸包的下边界),很容易发现当截距确定后,红色边界上面的点产生的截距小于红色边界上的点。那么我们该如何去找,我们确定i之后实际还需要sc[i]和dp[j]才能求出我们需要的值。如图中的绿线,它经过的点,显然是从下边界中找到两个斜率,一个大于它,一个小于它,由此确定出它经过哪个点。那么如果我们维护出一个存斜率的单调队列,就很容易查找目标位置,可以用二分来查找。
但是再观察一下式子,我们会发现(st[i]+s)和sc[j]都随着j的变大而变大,所以很明显,当前的斜率如果大于一部分斜率的话,那么后面的只会更大,所以前面的根本不会再被访问到,那么就没有存下来的意义,于是我们实际可以在O(1)的时间复杂度内完成查找。
这么来说,每个点可以通过的线有很多条,现在已知有哪些点了,需要找出一条斜率已知的直线通过哪个点的截距最小,显然可以通过维护已知点的下凸壳得到,另外,凸壳边的斜率不等价于将这个点放入时的直线斜率。所以尽管放入的点对应的直线的斜率越来越大,但是凸壳的斜率也会有大于和小于的。当然如图中的绿线,这个点被放入后,k2线后面的两个点便不会再作为结果中的点了,因为有更合适的点出现了。
所以我们查询和放入时的删除操作不同,查询的时候,是这么考虑的,如果k1没被用到,也即k1<k,那么后续放入的线的k只会更大,那么至少得从2开始找(因为当前这个小于k2),所以压根用不到k1,那么我们是将点1弹出。
在放入的时候,很显然当前的绿线一旦放入,点3和点4就不会再作为凸壳的边了,因为新放入的点显然与2之间连的边变成凸壳的下边界了。
所以我们查询的时候是按照凸壳的边来查询的,修改的时候修改的也是凸壳的边,所以我们实际上维护的是凸壳下边界。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll t[300010],c[300010],dp[300010],q[300010],hh,tt;
int main()
{
int n,s;
scanf("%d%d",&n,&s);
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&t[i],&c[i]);
t[i]+=t[i-1];
c[i]+=c[i-1];
}
hh=0,tt=1;//0是需要被放入的
for(int i=1;i<=n;i++)
{
while(hh<tt&&(dp[q[hh+1]]-dp[q[hh]])<(c[q[hh+1]]-c[q[hh]])*(t[i]+s) ) hh++;
int j=q[hh];
dp[i]=dp[j]-(t[i]+s)*c[j]+c[i]*t[i]+s*c[n];
//这一步要保证队列中至少有两个元素,否则直接放入即可
while(hh+1<tt&&(dp[q[tt-1]]-dp[q[tt-2]])*(c[i]-c[q[tt-2]])>=(dp[i]-dp[q[tt-2]])*(c[q[tt-1]]-c[q[tt-2]])) tt--;
q[tt++]=i;
}
cout<<dp[n];
}一定要明确的就是凸壳的斜率和点 被放入时对应的直线斜率不是一回事,凸壳的斜率只是用来辅助查找点的,与直线斜率没有直接关系,另外凸壳的斜率的维护也要注意,查询和插入对应的是不同的修改策略。
302. 任务安排3(302. 任务安排3 - AcWing题库)

思路:这题变化的地方在于t的范围,t可能为负值, 范围很大很明显没有办法暴力,那么还是来考虑优化:
dp[j]=(st[i]+s)*sc[j]+dp[i]-sc[i]*st[i]-s*sc[n];
这里直线的斜率由于t为负,那么就可能就不是单增了,所以在查询的时候是没办法修改的,因为当前的直线没用到凸壳的某个斜率,不代表后面的直线不会用到,但是凸壳仍然是维护一个单增的序列(这个应该是凸壳的性质。)直线斜率为负也没关系,仍然是找第一个大于直线斜率的凸壳斜率,所以不用担心,如下图:
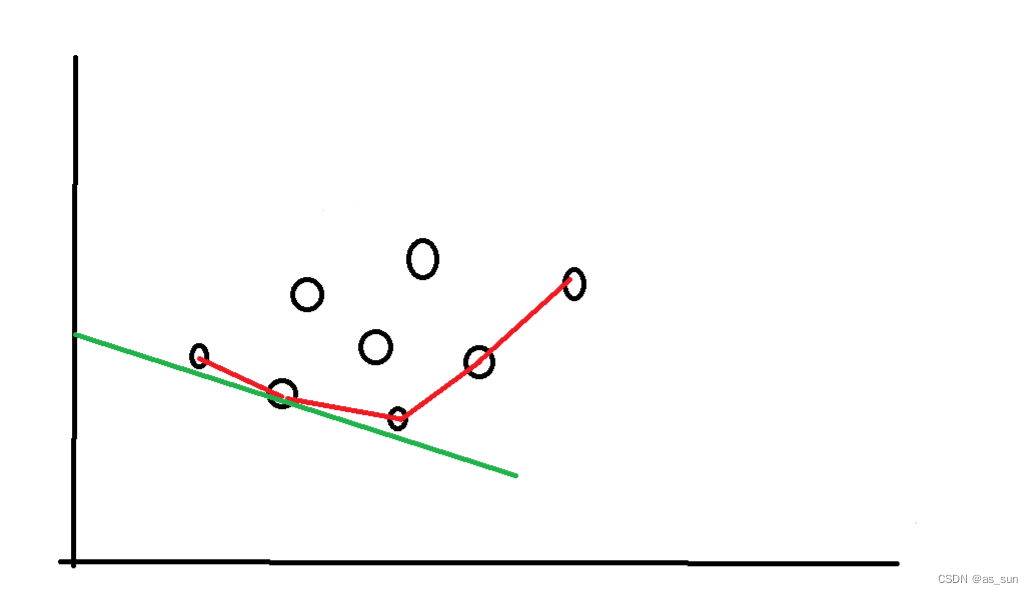
所以相当于这里凸壳的维护不做更改,仅仅查询改变一下即可。也就是通过二分来查询符合要求的点,然后修改的维护同前。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll t[300010],c[300010],dp[300010],q[300010],hh,tt;
int main()
{
int n,s;
scanf("%d%d",&n,&s);
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&t[i],&c[i]);
t[i]+=t[i-1];
c[i]+=c[i-1];
}
hh=0,tt=1;//0是需要被放入的
for(int i=1;i<=n;i++)
{
int l=hh,r=tt-1;
while(l<r)
{
int mid=(l+r)/2;
if((dp[q[mid+1]]-dp[q[mid]])>=(c[q[mid+1]]-c[q[mid]])*(t[i]+s) ) r=mid;
else l=mid+1;
}
int j=q[l];
dp[i]=dp[j]-(t[i]+s)*c[j]+c[i]*t[i]+s*c[n];
//这一步要保证队列中至少有两个元素,否则直接放入即可
while(hh+1<tt&&(double)(dp[q[tt-1]]-dp[q[tt-2]])*(c[i]-c[q[tt-2]])>=(double)(dp[i]-dp[q[tt-2]])*(c[q[tt-1]]-c[q[tt-2]])) tt--;
q[tt++]=i;
}
cout<<dp[n];
}ps:这里相乘那一块儿有可能溢出long long,故而使用double
摘自网上资料:
其实double可以存储比unsigned long long更大的数字原因是无符号 long long 会存储精确整数,而 double 存储尾数有限的精度和一个指数。
这允许 double 存储非常大的数字(大约10^308 ),一个 double 中有大约15个(近16个)有效的十进制数字,其余的可能的小数是零(实际上是未定义的,但是你可以假定为”零”更好的理解)。
一个无符号long long 只有19个数字,但是每一个数字都被精确定义。
也就是说double的精度(15或16位)比long long(19位)位要小,但是由于double只表示十进制的15或16位有效数字和它的指数,所以负值取值范围为 -1.7976E+308 到 -4.94065645841246544E-324,正值取值范围为 4.94065645841246544E-324 到 1.797693E+308。
对于long long
其64位的范围应该是[-2^63 ,2^63],既-9223372036854775808~9223372036854775807。
它的存储方法就是按位存储。有符号位就有一位符号位,没有符号位就64位全部来存储这个数。正是double不同于long long的存储方法,使得它虽然只有64位但是可以比同样是64位的long long 类型取值范围大很多。
303. 运输小猫(303. 运输小猫 - AcWing题库)


题目大意:现在有m只猫,在n座山上玩,已知相邻两座山的间距,以及每只猫在哪座山上的游玩时间,一旦游玩结束,猫就变成等待状态,饲养员从1号山出发去接猫,只能接在等待状态的猫,其余的猫都不可以被接走。求猫的等待时间的最小和。
我们可以通过山的间距算出每座山到1的距离,又因为速度是1m/s,那么距离和时间相当于1:1的关系,设出发时间为s,那么到达第i座山的时间就是s+di,这座山上的某只猫的玩耍时间为ti的话,那么ti + wi=s+di,所以对每只猫来说,如果不用等待,那么显然s=ti-di,这即饲养员的最早出发时间,它的自身属性相当于就是ai=ti-di,另外注意到,饲养员的出发时间可以为负值,所以di>ti也无所谓。那么分析到这里,看似又没办法继续分析了。这里既然有这么多猫,我们按照ai排个序看看,因为我们排序的依据时每只猫恰好被接走时饲养员的最早出发时间,那么我们要一次接走一整段上的猫,肯定要以这段中的最晚时间为准,那么这段中猫的等待时间则为(ai-a1)+(ai-a2)+...+(ai-ai),所以我们可以将猫分段,那么这个问题就与我们之前的问题有些关联了。
定义dp[i][j]表示第i只猫恰好被第j个饲养员收走,我们可以通过找上一段猫的结尾位置来更新状态:
dp[i][j]=dp[k][j-1]+ai*(i-k+1)-(a[k+1]+a[k+2]+...+a[i])
令s[i]=a[1]+a[2]+...+a[i]:
则:dp[i][j]=dp[k][j-1]+ai(i-k+1)-(s[i]-s[k]);
移项可得:
dp[i][j]-ai*(i-k+1)+s[i]=dp[k][j-1]+s[k]
dp[k][j-1]+s[k]=a[i]*k+dp[i][j]-a[i]*(i+1)+s[i];
那么就跟上题关联起来了,而且这里的a[i]单增,我们甚至都不需要用二分来查找。
哦对了,另外,为了优化程序我们改一下两个维度,定义dp[j][i],因为我们循环的第一维是j的那一维,这样定义的话,磁盘读取会快一些。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010,M=100010,P=110;
ll t[N],d[N],a[N],s[N];
ll dp[P][M];
int q[M],hh,tt;
ll get(int i,int j)
{
return dp[j-1][i]+s[i];
}
int main()
{
int n,m,p;
scanf("%d%d%d",&n,&m,&p);
for(int i=2;i<=n;i++)
{
scanf("%lld",&d[i]);
d[i] += d[i-1];
}
for(int i=1;i<=m;i++)
{
int h;
scanf("%d%lld",&h,&t[i]);
a[i]=t[i]-d[h];
}
sort(a+1,a+1+m);
for(int i=1;i<=m;i++) s[i]=s[i-1]+a[i];
memset(dp,0x3f,sizeof dp);
for(int i=0;i<=p;i++) dp[i][0]=0;
for(int j=1;j<=p;j++)
{
//dp[k][j-1]+s[k]=a[i]*k+dp[i][j]-a[i]*(i+1)+s[i];
hh=0,tt=1;
q[0]=0;
for(int i=1;i<=m;i++)
{
while(hh+1<tt&&(get(q[hh+1],j)-get(q[hh],j))<=a[i]*(q[hh+1]-q[hh])) hh++;
int k=q[hh];
dp[j][i]=dp[j-1][k]+a[i]*(i-k)-(s[i]-s[k]);
while(hh+1<tt&&(get(q[tt-1],j)-get(q[tt-2],j))*(i-q[tt-1])>=
(get(i,j)-get(q[tt-1],j))*(q[tt-1]-q[tt-2])) tt--;//我们维护的是上一层,所以这里是get(i,j)
q[tt++]=i;
}
}
cout<<dp[p][m];
}ps:这里查询的时候就要严格保证队列中至少有两个元素再进循环,因为队列重复使用,没清。
斜率优化dp主要有两种类型,都是首先将状态转移的式子变形成一个一元函数,然后通过斜率与截距的关系来优化。
优化涉及到两种类型,一种是斜率和自变量都单增,那么维护单调队列即可实现查找,一种是仅自变量单增,那么就需要用二分来查找,另外凸包下边界的维护对于两者来说是一样的。