介绍： 

## Flow chart for a simple neural network:

#(1)Take inputs 输入
#(2)Add bias (if required)
#(3)Assign random weights to input features 随机一个权重
#(4)Run the code for training. 训练集训练
#(5)Find the error in prediction. 找预测损失
#(6)Update the weight by gradient descent algorithm. 根据梯度下降更新权重
#(7)Repeat the training phase with updated weights. 重复训练更新权重
#(8)Make predictions. 做预测

 

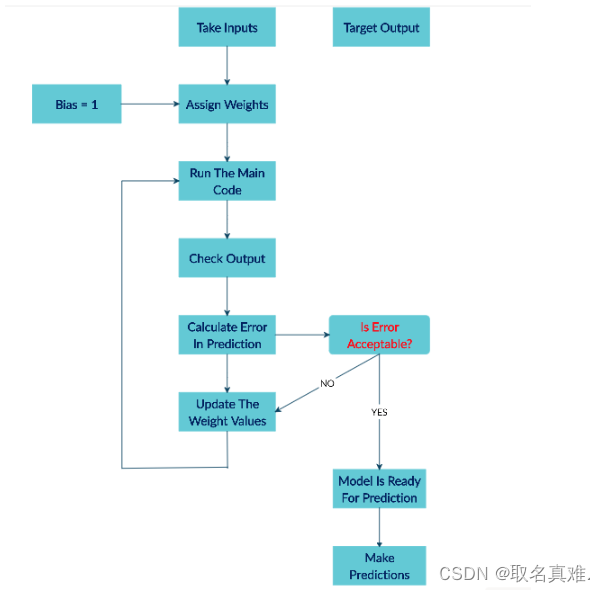
参考： 深度学习使用python建立最简单的神经元neuron-CSDN博客

 数据：

# Import the required libraries
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

# Load the data
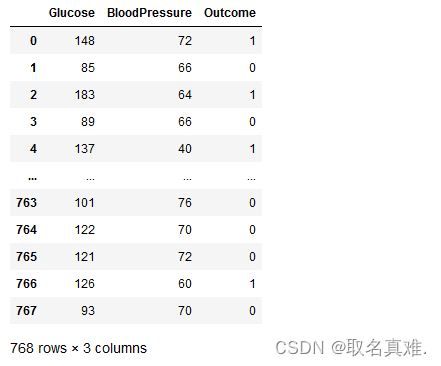
df = pd.read_csv('Lesson44-data.csv') 
df

一、

# Separate the features and label
x = df[['Glucose','BloodPressure']]#特征值
y = df['Outcome']#标签

三、

np.random.seed(10)#初始化
label = y.values.reshape(y.shape[0],1)
weights = np.random.rand(2,1)#随机一个权重
bias = np.random.rand(1)
learning_rate = 0.0000004#梯度下降步长
epochs = 1000 #迭代次数

四~七、

# Define the sigmoid function
def sigmoid(input):    
    output = 1 / (1 + np.exp(-input))
    return output



# Define the sigmoid derivative function基于sigmoid导数
def sigmoid_derivative(input):
    return sigmoid(input) * (1.0 - sigmoid(input))




def train_network(x,y,weights,bias,learning_rate,epochs):  #Epochs. 来回 One Epoch is when an ENTIRE dataset is passed forward and backward through the neural network only ONCE.
    j=0                                                    #weights 权重
    k=[]                                                   #learning_rate梯度下降的步长
    l=[]
    for epoch in range(epochs):       
        dot_prod = np.dot(x, weights) + bias#np.dot矩阵乘积
        # using sigmoid
        preds = sigmoid(dot_prod)
        # Calculating the error
        errors = preds - y  #计算错误，预测-实际
        # sigmoid derivative
        deriva_preds = sigmoid_derivative(preds)
        deriva_product = errors * deriva_preds
        #update the weights
        weights = weights -  np.dot(x.T, deriva_product) * learning_rate
        loss = errors.sum()
        j=j+1
        k.append(j)
        l.append(loss)
        print(j,loss)
    for i in deriva_product:
        bias = bias -  i * learning_rate
    plt.plot(k,l)
    return weights,bias

weights_final, bias_final = train_network(x,label,weights,bias,learning_rate,epochs)

八、

weights_final
'''结果：
array([[ 0.06189634],
       [-0.12595182]])
'''

bias_final
#结果：array([0.633647])

# Prediction
inputs = [[101,76]]
dot_prod = np.dot(inputs, weights_final) + bias_final
preds = sigmoid(dot_prod) >= 1/2
preds
#结果：array([[False]])

inputs = [[137,40]]
dot_prod = np.dot(inputs, weights_final) + bias_final
preds = sigmoid(dot_prod) >= 1/2
preds
#结果：array([[ True]])